Динамическое программирование на скорости GPU: новый подход к оптимизации

от

Автор: Денис Аветисян

Исследователи разработали метод, позволяющий значительно ускорить решение сложных задач комбинаторной оптимизации, используя возможности графических процессоров.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал
Параллельное вычисление на графическом процессоре позволяет эффективно исследовать пространство предшественников для каждой целевой конфигурации, формируя множество [latex]\{J^{\omega}(p)+A^{\omega}(p,i):\,p<i\}[/latex] путём одновременной обработки всех предшественников [latex]p<i[/latex] и последующего минимизирования по столбцам, что позволяет определить [latex]J^{\omega}(i)[/latex] для каждой конфигурации [latex](i,\omega)[/latex].
Параллельное вычисление на графическом процессоре позволяет эффективно исследовать пространство предшественников для каждой целевой конфигурации, формируя множество \{J^{\omega}(p)+A^{\omega}(p,i):\,p<i\}[ [latex](i,\omega)[="" [latex]j^{\omega}(i)[="" [latex]p<i[="" figcaption="" latex]="" latex].<="" всех="" для="" и="" каждой="" конфигурации="" минимизирования="" обработки="" одновременной="" определить="" по="" позволяет="" последующего="" предшественников="" путём="" столбцам,="" что=""> </i\}[></figcaption></figure> <p><b>В статье представлен GPU-ускоренный фреймворк для эффективного решения крупномасштабных стохастических задач комбинаторной оптимизации, основанный на переформулировке динамического программирования для оценки вторых этапов с учетом сценариев.</b></p> <p>Несмотря на возрастающую сложность задач стохастической оптимизации, традиционные методы часто сталкиваются с ограничениями масштабируемости при работе с крупными наборами сценариев. В данной работе, озаглавленной <i>'From Sequential to Parallel: Reformulating Dynamic Programming as GPU Kernels for Large-Scale Stochastic Combinatorial Optimization'</i>, предложен GPU-ускоренный фреймворк, позволяющий эффективно решать задачи динамического программирования во вторичных оценках при рекурсивных сценариях. Ключевым достижением является экспоненциальное ускорение вычислений и возможность решения задач, ранее считавшихся непрактичными, в областях, таких как маршрутизация транспорта и управление запасами. Не откроет ли это путь к созданию более реалистичных и эффективных моделей для крупномасштабной стохастической дискретной оптимизации?</p> <hr/> <h2>Неопределенность спроса: вызов современной логистике</h2> <p>Традиционные решения в области маршрутизации транспортных средств часто сталкиваются с проблемой непредсказуемости реального спроса, что приводит к значительным неэффективностям и увеличению издержек. В отличие от упрощенных моделей, предполагающих стабильный и предсказуемый объем заказов, реальные логистические задачи характеризуются колебаниями спроса, вызванными различными факторами - от сезонности и акций до внезапных изменений в предпочтениях потребителей. Это несоответствие приводит к перегрузке одних транспортных средств и недозагрузке других, увеличивая общие транспортные расходы, время доставки и даже приводя к срыву сроков выполнения заказов. В результате, компании сталкиваются с необходимостью либо нести дополнительные издержки, связанные с неоптимальной маршрутизацией, либо рискуют потерять клиентов из-за некачественного обслуживания.</p> <p>Задача маршрутизации транспортных средств с учетом стохастического спроса (CVRPSD) представляет собой серьезную оптимизационную проблему, обусловленную как ее вычислительной сложностью, так и необходимостью анализа вероятностных сценариев. В отличие от классических задач, где спрос в каждой точке известен заранее, CVRPSD требует учета неопределенности - спрос является случайной величиной. Это значительно усложняет процесс планирования маршрутов, поскольку необходимо найти решения, которые будут эффективны не только для одного конкретного сценария спроса, но и в среднем, для всех возможных реализаций. Поиск оптимального решения требует разработки специальных алгоритмов и методов, способных эффективно обрабатывать вероятностные данные и оценивать риски, связанные с неточным прогнозированием спроса. Решение CVRPSD позволяет значительно снизить транспортные расходы и повысить уровень обслуживания клиентов, обеспечивая надежную доставку даже в условиях высокой неопределенности.</p> <figure> <img alt="Двухэтапная стохастическая оптимизация позволяет разработать план доставки и маршрутизации на первый день с учетом ограничений по вместимости транспортных средств, а затем адаптировать решения на последующие дни, реагируя на реализованный спрос в каждом сценарии, для минимизации общих ожидаемых затрат, включающих затраты на маршрутизацию, хранение запасов и штрафы за дефицит." src="https://arxiv.org/html/2602.05179v1/figure/2-stage.png" style="background-color: white;"/ referrerpolicy="no-referrer"><figcaption>Двухэтапная стохастическая оптимизация позволяет разработать план доставки и маршрутизации на первый день с учетом ограничений по вместимости транспортных средств, а затем адаптировать решения на последующие дни, реагируя на реализованный спрос в каждом сценарии, для минимизации общих ожидаемых затрат, включающих затраты на маршрутизацию, хранение запасов и штрафы за дефицит.</figcaption></figure> <h2>Стохастическое программирование: устойчивые решения в условиях неопределенности</h2> <p>Стохастическое программирование представляет собой мощный инструментарий для включения неопределенности в модели оптимизации, позволяющий создавать решения, устойчивые к различным реализациям спроса. В отличие от детерминированных моделей, предполагающих известные значения параметров, стохастическое программирование учитывает вероятностный характер входных данных, таких как объемы заказов или время обслуживания. Это достигается путем моделирования различных возможных сценариев и оптимизации решения, которое минимизирует ожидаемые затраты или максимизирует ожидаемую прибыль во всех этих сценариях. Ключевым аспектом является использование вероятностных распределений для представления неопределенности и применение методов решения, адаптированных к работе с этими распределениями, что позволяет получить более надежные и реалистичные результаты по сравнению с традиционными подходами.</p> <p>Формулирование задачи CVRPSD (Capacity Constrained Vehicle Routing Problem with Stochastic Demands) в рамках стохастического программирования позволяет минимизировать математическое ожидание суммарных затрат при различных реализациях случайных величин, представляющих спрос клиентов. Метод Scenario-Based SP (стохастическое программирование на основе сценариев) предполагает создание конечного набора сценариев, описывающих вероятные исходы спроса, и оптимизацию решения для всех этих сценариев одновременно. Это достигается путем построения детерминированной модели, включающей переменные, связанные с каждым сценарием, и целевой функции, представляющей собой взвешенную сумму затрат по всем сценариям, где веса соответствуют вероятностям реализации каждого сценария. [latex]E[C] = \sum_{i=1}^{N} p_i C_i, где E[C] - математическое ожидание затрат, p_i - вероятность реализации сценария i, а C_i - затраты при сценарии i. Использование такого подхода обеспечивает получение решений, устойчивых к колебаниям спроса и позволяющих снизить общие ожидаемые затраты на логистику.

Динамическое программирование в рамках стратегии Order-Up-To позволяет систематически вычислять стоимость различных путей пополнения запасов, учитывая возможные состояния и переходы между ними, при этом недостижимые переходы обозначаются как [latex] +\in fty [/latex], что позволяет интегрировать этот алгоритм в любые эвристические или метаэвристические методы.
Динамическое программирование в рамках стратегии Order-Up-To позволяет систематически вычислять стоимость различных путей пополнения запасов, учитывая возможные состояния и переходы между ними, при этом недостижимые переходы обозначаются как +\in fty , что позволяет интегрировать этот алгоритм в любые эвристические или метаэвристические методы.

Ускорение решений с помощью GPU-декомпозиции

Вычислительная сложность решения задачи CVRPSD со стохастическим программированием значительно снижается при использовании GPU-ускорения для оптимизации процесса решения. Использование графических процессоров позволяет параллельно выполнять большое количество операций, что критически важно для обработки больших объемов данных и сложных вычислений, характерных для стохастических моделей. Это приводит к существенному сокращению времени, необходимого для получения оптимальных или близких к оптимальным решений, что делает возможным практическое применение алгоритмов стохастической оптимизации в задачах, требующих высокой скорости реагирования и обработки больших объемов информации.

Комбинация оператора разделения (Split Operator) с GPU-ускоренным алгоритмом SPLIT позволяет декомпозировать крупные маршруты на более управляемые участки, что значительно повышает вычислительную эффективность. Данный подход разбивает сложную задачу маршрутизации на серию более простых подзадач, которые могут быть решены параллельно на графическом процессоре. Разделение маршрутов уменьшает объем вычислений, необходимых для каждого этапа оптимизации, и позволяет эффективно обрабатывать задачи с большим количеством клиентов и транспортных средств, обеспечивая существенное ускорение процесса решения.

Разработанный фреймворк использует коммерческий решатель Gurobi в рамках модели целочисленного линейного программирования (MILP) для эффективного решения оптимизационной задачи. Проведенные тесты демонстрируют ускорение решения до 5 порядков величины (в 80 раз) по сравнению с реализациями на центральных процессорах (CPU) для задач CVRPSD и DSIRP. Это значительное увеличение производительности позволяет существенно сократить время вычислений и решать более сложные задачи оптимизации транспортной логистики.

Разработанная платформа обеспечивает возможность оценки более 1,000,000 сценариев, что критически важно для получения надежных стохастических решений в задачах оптимизации. Возможность анализа такого объема данных позволяет учитывать неопределенности и вариабельность параметров, что повышает устойчивость и эффективность полученных планов маршрутизации и распределения ресурсов. Оценка большого количества сценариев позволяет минимизировать риски, связанные с непредсказуемыми событиями, и оптимизировать решения для различных возможных условий.

Параллелизм на GPU позволяет эффективно решать задачу динамического программирования, одновременно обрабатывая различные сценарии, переходы между состояниями и варианты маршрутизации, что приводит к пакетной минимизации затрат и обновлению стоимости [latex]J_{i}^{t+1}(J)[/latex] с учетом штрафов за хранение и дефицит.
Параллелизм на GPU позволяет эффективно решать задачу динамического программирования, одновременно обрабатывая различные сценарии, переходы между состояниями и варианты маршрутизации, что приводит к пакетной минимизации затрат и обновлению стоимости J_{i}^{t+1}(J) с учетом штрафов за хранение и дефицит.

Расширение горизонтов: динамическое стохастическое управление запасами и маршрутизацией

Интеграция управления запасами с маршрутизацией транспортных средств приводит к возникновению сложной задачи - Динамической Стохастической Проблеме Маршрутизации и Управления Запасами (DSIRP). Традиционно эти две области рассматривались отдельно, однако реальные логистические цепочки требуют одновременной оптимизации как уровня запасов на складах, так и маршрутов доставки. DSIRP учитывает неопределенность спроса и времени доставки, что делает ее существенно более сложной, чем стандартные задачи маршрутизации или управления запасами. По сути, решается задача определения оптимального количества товара для пополнения запасов на каждом складе и одновременного планирования маршрутов для транспортных средств, доставляющих эти товары, с учетом изменяющихся условий и вероятностных факторов. Это требует разработки новых алгоритмов и подходов, способных эффективно обрабатывать большое количество переменных и ограничений, а также учитывать стохастическую природу логистических процессов.

Для эффективного решения динамической стохастической задачи маршрутизации и управления запасами (DSIRP) применяются методы динамического программирования, значительно ускоренные за счет использования графических процессоров (GPU). Традиционные алгоритмы часто сталкиваются с вычислительной сложностью при увеличении масштаба задачи и неопределенности спроса. Использование GPU позволяет распараллеливать вычисления, существенно сокращая время обработки и обеспечивая возможность получения оптимальных решений даже для крупных и сложных сценариев. Данный подход позволяет преодолеть ограничения традиционных методов и открывает путь к созданию более эффективных логистических систем, способных адаптироваться к изменяющимся условиям и минимизировать общие затраты.

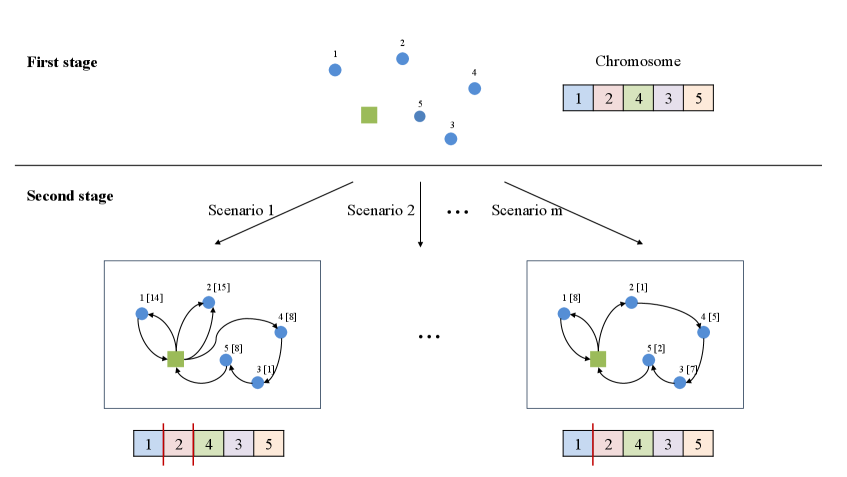
Разработанная методика объединяет стратегию пополнения запасов до определенного уровня (Order-Up-To Policy) с передовыми алгоритмами маршрутизации и оптимизации, формируя комплексное решение для управления как складскими запасами, так и транспортными издержками. Результаты исследований демонстрируют, что предложенный подход позволяет достичь улучшения целевой функции на 4.21% - 6.37% по сравнению с существующими передовыми методами решения задачи динамической стохастической маршрутизации с учетом управления запасами (DSIRP). Это свидетельствует о высокой эффективности разработанного фреймворка в оптимизации логистических процессов и снижении общих затрат, что делает его перспективным инструментом для предприятий, стремящихся к повышению эффективности управления цепями поставок.

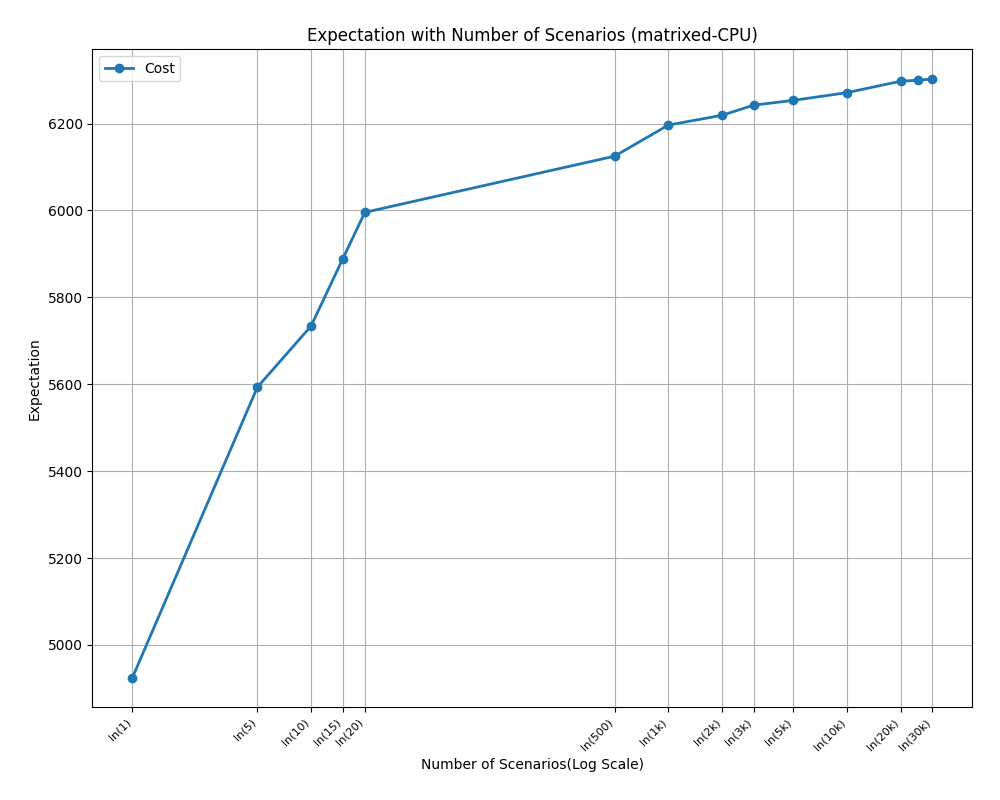
Разработанная структура демонстрирует впечатляющую масштабируемость, приближающуюся к линейной, при увеличении количества рассматриваемых сценариев. Это означает, что вычислительные затраты растут лишь незначительно с добавлением каждого нового сценария, что особенно важно для практического применения в сложных логистических системах. Такая эффективность достигается за счет оптимизированных алгоритмов и использования параллельных вычислений, позволяющих обрабатывать большое количество данных без существенного увеличения времени решения. Возможность эффективного масштабирования открывает перспективы для моделирования более реалистичных и комплексных ситуаций, учитывающих широкий спектр неопределенностей и факторов, влияющих на управление запасами и маршрутизацию транспорта.

Экспериментальные данные показывают, что оценка SAA в DSIRP демонстрирует смещение, зависящее от распределения спроса, и сходится к оптимальному решению с увеличением количества сценариев.
Экспериментальные данные показывают, что оценка SAA в DSIRP демонстрирует смещение, зависящее от распределения спроса, и сходится к оптимальному решению с увеличением количества сценариев.

Перспективы развития: интеграция альтернативных подходов

Несмотря на то, что методы целочисленного линейного программирования (MILP) и динамическое программирование предоставляют мощные инструменты для решения задач, альтернативные подходы, такие как генетические алгоритмы и метод Монте-Карло, играют важную роль в оценке различных сценариев. Эти методы позволяют оценить устойчивость полученных решений к изменениям входных данных и неопределенностям, что особенно важно в реальных логистических системах. В отличие от точных методов, генетические алгоритмы и метод Монте-Карло не гарантируют нахождение оптимального решения, но позволяют быстро исследовать большое количество возможных вариантов и оценить их эффективность в различных условиях, выявляя наиболее надежные и робастные стратегии маршрутизации и управления запасами. Таким образом, комбинация точных и эвристических методов позволяет получить более полное и реалистичное представление о работе системы.

Сочетание методов, таких как генетические алгоритмы и метод Монте-Карло, с уже существующими подходами математического программирования, формирует мощный и универсальный инструментарий для решения сложных задач маршрутизации транспорта и управления запасами. Данный комплексный подход позволяет не только находить оптимальные решения в различных сценариях, но и оценивать их устойчивость к внешним факторам, что особенно важно в динамичной среде современной логистики. Эффективное использование этих методов дает возможность охватить широкий спектр задач, начиная от оптимизации маршрутов доставки и заканчивая управлением складскими запасами, повышая эффективность и снижая затраты в цепи поставок.

Перспективные исследования направлены на создание интегрированных систем, способных к адаптации и самооптимизации в условиях динамично меняющегося спроса и предложения. Такие системы, объединяющие методы математического программирования, генетические алгоритмы и методы Монте-Карло, позволят не только находить оптимальные решения в текущий момент времени, но и прогнозировать их устойчивость к внешним факторам. Предполагается, что подобные адаптивные системы смогут автоматически перестраивать логистические маршруты и уровни запасов в режиме реального времени, учитывая колебания спроса, задержки поставок или другие непредвиденные обстоятельства, обеспечивая тем самым повышенную эффективность и надежность всей цепочки поставок.

Представленный пример демонстрирует разделение сложного маршрута на выполнимые участки с учетом заданного спроса.
Представленный пример демонстрирует разделение сложного маршрута на выполнимые участки с учетом заданного спроса.

Исследование, представленное в данной работе, демонстрирует значительный прогресс в области ускорения вычислений для стохастической комбинаторной оптимизации. Авторы успешно адаптировали принципы динамического программирования для параллельной обработки на графических процессорах (GPU), что позволило существенно повысить скорость решения крупномасштабных задач, таких как маршрутизация транспорта и управление запасами. Этот подход особенно важен, учитывая сложность анализа больших объемов данных и необходимость выявления закономерностей для эффективной оптимизации. Как однажды заметил Григорий Перельман: «Математика - это язык, на котором написана книга природы». Данное исследование подтверждает эту мысль, показывая, как математические инструменты, реализованные на современных вычислительных платформах, позволяют раскрыть скрытые закономерности и решать сложные практические задачи.

Куда двигаться дальше?

Представленная работа, демонстрируя возможности параллельного решения задач стохастической оптимизации посредством использования архитектуры GPU, не является, разумеется, финальной точкой. Скорее, это приглашение к более глубокому исследованию границ применимости динамического программирования в условиях неопределенности. Очевидным направлением является расширение спектра решаемых задач. Изначально ориентированные на маршрутизацию и управление запасами, методы требуют адаптации к более сложным моделям, включающим, например, многоуровневые системы принятия решений и динамически меняющиеся ограничения.

Однако, истинный вызов заключается не только в масштабируемости, но и в преодолении фундаментальных ограничений, присущих динамическому программированию. Поиск эффективных методов аппроксимации, позволяющих снизить вычислительную сложность без существенной потери точности, представляется задачей, достойной внимания. Ирония заключается в том, что ускорение вычислений лишь обнажает проблему "проклятия размерности", заставляя искать новые, более элегантные подходы к моделированию сложных систем.

В конечном итоге, успешное развитие данного направления требует не просто оптимизации алгоритмов, но и переосмысления самой парадигмы решения задач стохастической оптимизации. Возможно, будущее за гибридными методами, объединяющими преимущества динамического программирования с мощью современных алгоритмов машинного обучения, способными извлекать знания из данных и адаптироваться к меняющимся условиям.

Оригинал статьи: https://arxiv.org/pdf/2602.05179.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-06 19:24