Динамика сложных систем: новый подход к моделированию

Автор: Денис Аветисян

В статье представлен комплексный фреймворк на основе численного метода конечных элементов для анализа движения многокомпонентных систем с учетом контактных взаимодействий и вязкоупругих свойств.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Ключевые конфигурации элементов определяют основу для дальнейшей оптимизации и анализа систем, позволяя выявить наиболее эффективные и стабильные структуры.

Разработанный подход основан на тотальной лагранжевой формулировке и позволяет моделировать сложные системы с различными кинематическими ограничениями.

Несмотря на значительный прогресс в области численного моделирования, анализ динамики сложных многотельных систем с учетом больших деформаций и контактного взаимодействия остается сложной задачей. В данной работе, посвященной ‘The Kinematics and Dynamics Theories of a Total Lagrangian Finite Element Analysis Framework for Finite Deformation Multibody Dynamics’, предложена всеобъемлющая формулировка на основе конечно-элементного анализа с полным лагранжевым подходом для моделирования деформируемых тел. Разработанный метод позволяет последовательно учитывать кинематические ограничения, контактное взаимодействие и вязкоупругие свойства материалов, используя $\mathcal{N}$ -конечные элементы балки, оболочки и тетраэдры. Какие перспективы открывает данная методика для решения задач динамики сложных механизмов и робототехнических систем?

Точное моделирование: вечная борьба с вычислительными затратами

Точное моделирование деформации твердых тел является фундаментальной задачей во многих областях инженерии, включая автомобилестроение, авиакосмическую промышленность и биомеханику. Однако, достижение высокой точности сопряжено со значительными вычислительными трудностями. Сложность заключается в необходимости учета нелинейного поведения материалов, сложных геометрических форм и возможных контактов между различными частями конструкции. Для решения этих задач требуются передовые численные методы и мощные вычислительные ресурсы, способные эффективно обрабатывать огромные объемы данных и обеспечивать стабильные и достоверные результаты. Без точного моделирования деформации невозможно надежно прогнозировать поведение конструкций в различных условиях эксплуатации и гарантировать их безопасность и долговечность.

Традиционные методы конечных элементов, широко применяемые для моделирования деформации твердых тел, зачастую сталкиваются с существенными трудностями при работе с большими деформациями и сложными сценариями контакта. Проблема заключается в том, что стандартные алгоритмы могут терять точность или вовсе сходиться к неверному решению, когда геометрия объекта значительно изменяется или при взаимодействии с другими объектами возникает сложная контактная задача. Это требует разработки более устойчивых и эффективных формулировок, способных адекватно учитывать нелинейные эффекты и обеспечивать надежные результаты даже в самых сложных условиях. Повышение робастности и эффективности этих методов является ключевой задачей современной вычислительной механики, направленной на создание более реалистичных и точных моделей деформируемых тел.

Современные методы моделирования деформаций твердых тел зачастую сталкиваются с проблемой компромисса между вычислительными затратами и точностью, особенно при работе с нелинейными материалами и сложной геометрией объектов. Нелинейное поведение материалов, такое как пластичность или вязкоупругость, требует более сложных математических моделей и, следовательно, больше вычислительной мощности для их решения. Аналогично, моделирование объектов со сложной геометрией, включающей тонкие детали или острые углы, требует использования очень мелкой сетки, что экспоненциально увеличивает число необходимых вычислений. В результате, для получения достоверных результатов зачастую требуются значительные ресурсы, включая мощные компьютеры и продолжительное время расчетов, что ограничивает применимость этих методов в задачах, требующих оперативных решений или моделирования крупномасштабных систем. Поиск эффективных алгоритмов и численных методов, позволяющих снизить вычислительную сложность без потери точности, остается актуальной задачей современной механики сплошных сред.

Визуализация полностью параметризованного двухузельного балочного элемента [latex]ANCF[/latex] демонстрирует его конструкцию и гибкость. — Визуализация полностью параметризованного двухузельного балочного элемента $ANCF$ демонстрирует его конструкцию и гибкость.

Полная лагранжевая формулировка: надежная основа для сложных деформаций

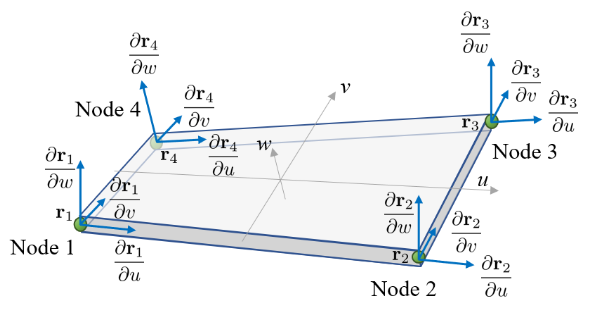
Формулировка полной лагранжевой механики обеспечивает надежную основу для анализа задач с большими деформациями, поскольку все вычисления привязаны к исходной, недеформированной конфигурации. Это означает, что координаты узлов, векторы касательных и нормали, а также матрицы жесткости и деформаций определяются в исходном состоянии, что позволяет избежать проблем, связанных с геометрической нелинейностью при больших перемещениях. Использование исходной конфигурации упрощает формулировку уравнений движения и обеспечивает стабильность численных решений, особенно при моделировании процессов, включающих значительные изменения геометрии тела. В рамках данной формулировки, деформации рассчитываются как разница между текущим положением узла и его исходным положением, что позволяет корректно учитывать эффекты нелинейной геометрии и материалов.

Формулировка предполагаемых деформаций, интегрированная с элементом ANCF (Absolute Nodal Coordinate Formulation), повышает точность и эффективность расчетов за счет введения предопределенного поля деформаций. Вместо вычисления деформаций непосредственно из перемещений узлов, предполагаемые деформации задаются в виде функций от координат узлов и параметров элемента. Это позволяет уменьшить количество степеней свободы, необходимых для описания деформации, и улучшить сходимость решения, особенно при анализе задач с крупными деформациями и сложной геометрией. Использование предполагаемых деформаций также позволяет избежать блокировки деформаций, возникающей в стандартных формулировках конечных элементов при моделировании несжимаемых материалов. Предполагаемые деформации обычно строятся на основе кинематических предположений о характере деформирования, таких как линейные или квадратичные функции от координат узлов, что позволяет эффективно описывать различные типы деформаций, например, изгиб, растяжение и сдвиг.

Комбинация тотальной лагранжевой формулировки и элементов ANCF (Assumed Strain) формирует мощную и универсальную конечно-элементную основу, способную моделировать сложные сценарии, включающие балки, оболочки и твердые тела с высокой точностью. Данный подход позволяет эффективно решать задачи с большими деформациями, обеспечивая стабильность и сходимость расчетов для различных геометрических конфигураций и материалов. Преимущества заключаются в возможности точного учета нелинейных эффектов, таких как геометрическая нелинейность и нелинейное материальное поведение, что критически важно для моделирования сложных конструкций и процессов. $\epsilon = \frac{1}{2} (\nabla u + (\nabla u)^T)$ — пример используемой деформационной модели.

Визуализация показывает полностью параметризованный 4-узловой элемент оболочки ANCF, состоящий из 3443 единиц.

Материалы и контакт: реалистичное поведение в сложных условиях

В рамках данной системы используются усовершенствованные модели материалов, в частности, модель Муни-Ривлина, для точного описания нелинейного поведения материалов, превосходящего возможности модели Сен-Венана-Кирхгофа. Модель Сен-Венана-Кирхгофа предполагает линейно-упругое поведение и имеет ограниченную применимость при больших деформациях. В отличие от неё, модель Муни-Ривлина, являясь гиперупругой, описывает нелинейную зависимость между напряжением и деформацией, что позволяет адекватно моделировать поведение материалов, подвергающихся значительным растяжениям и сжатиям, например, резины или эластомеров. Она характеризуется двумя параметрами, $C_{10}$ и $C_{01}$ , определяющими жесткость при одноосном и двуосном растяжении соответственно, и позволяет более реалистично симулировать деформацию и напряжение в сложных механических системах.

Реалистичное моделирование контакта в рамках данной системы достигается за счет использования как закона Герца для определения нормальных сил контакта, так и модели Майндлина, учитывающей историю деформаций и позволяющей рассчитывать как нормальные, так и тангенциальные силы. Закон Герца применяется для определения силы реакции при упругом контакте двух тел, в то время как модель Майндлина расширяет эту концепцию, вводя учет проскальзывания и трения между контактирующими поверхностями. Это позволяет более точно моделировать поведение материалов при динамических нагрузках и в условиях сложного контакта, учитывая как упругие, так и диссипативные эффекты, возникающие из-за тангенциальных сил.

Интеграция затухания Кельвина-Фойгта обеспечивает диссипацию энергии в динамических симуляциях, повышая их стабильность и устойчивость. Данный подход позволяет эффективно гасить колебания и предотвращать численные расхождения, особенно при моделировании сложных взаимодействий. Коэффициент затухания $γt = -2\sqrt(5/6)β\sqrt(meffkt)$ определяет интенсивность диссипации, где β — параметр демпфирования, $meff$ — эффективная масса, а $kt$ — жесткость системы. Численное значение коэффициента позволяет точно контролировать уровень затухания в симуляции, оптимизируя ее поведение и обеспечивая реалистичные результаты.

Универсальность: гибкость и эффективность в различных задачах

Реализация данной формулировки охватывает широкий спектр конечных элементов, включая двухузловой элемент ANCF 3243 для моделирования балок и четырехузловой элемент ANCF 3443 для работы с оболочками. Такой подход позволяет эффективно решать задачи, связанные с деформацией и напряжением в различных конструкциях, обеспечивая гибкость в моделировании сложных инженерных систем. Использование элементов ANCF (Absolute Nodal Coordinate Formulation) гарантирует высокую точность и стабильность расчетов даже при значительных деформациях, что особенно важно для анализа нелинейного поведения материалов и конструкций. Благодаря универсальности применяемых элементов, методика может быть адаптирована к широкому кругу задач, от анализа строительных конструкций до моделирования динамики механизмов.

Разработка десятиузельного тетраэдрического элемента значительно расширяет возможности моделирования твердых тел в рамках данной системы. Этот элемент позволяет эффективно решать широкий спектр инженерных задач, от анализа напряжений и деформаций в сложных конструкциях до моделирования процессов формоизменения материалов. Благодаря своей гибкости и точности, он обеспечивает надежный инструмент для проектирования и оптимизации изделий в различных отраслях промышленности, включая автомобилестроение, авиакосмическую технику и строительство. Включение данного элемента в состав системы предоставляет пользователям комплексный набор инструментов для моделирования самых разнообразных физических явлений в твердых телах, обеспечивая высокую степень детализации и реалистичности результатов.

Разработанная модульная конструкция позволяет создавать индивидуальные решения, оптимизируя вычислительную эффективность и точность в зависимости от конкретных требований каждой симуляции. В отличие от явных методов, использование неявной временной интеграции становится возможным, что значительно увеличивает допустимый шаг по времени и, как следствие, сокращает общее время вычислений, особенно при моделировании динамических процессов. Гибкость данной архитектуры позволяет инженерам выбирать наиболее подходящие элементы и методы решения для каждой задачи, избегая излишних вычислительных затрат и обеспечивая высокую достоверность результатов моделирования. Данный подход особенно ценен при решении сложных инженерных задач, требующих компромисса между точностью и скоростью вычислений.

Изображение демонстрирует тетраэдрический элемент, состоящий из 10 узлов.

В статье описывается очередная попытка обуздать сложность динамики многотельных систем с помощью тотального лагранжевого метода конечных элементов. Изящно, конечно, но всегда найдутся силы трения и нелинейности, которые сведут все расчеты к приближениям. Вспоминается, как раньше довольствовались упрощенными моделями, и всё работало. А теперь — контактная механика, вязкоупругость, кинематические ограничения… Кажется, каждый новый алгоритм — это просто попытка замаскировать старые баги под видом инноваций. Как метко заметил Винтон Серф: «Интернет — это просто способ передавать файлы». В данном случае, эта сложная система — лишь способ переложить задачу расчета на плечи компьютера, не решив её по-настоящему.

Что дальше?

Представленная работа, безусловно, расширяет инструментарий для моделирования многочастичных систем. Однако, каждая «революционная» возможность — контакт, вязкоупругость, сложные кинематические связи — это лишь новые векторы для возникновения ошибок. Теоретическая элегантность неизбежно столкнётся с жестокой реальностью продакшена, где данные будут неполными, а вычислительные ресурсы — ограниченными. Предсказывается, что отладка этих систем потребует молитв, обращенных к богам CI/CD, в храме, где мы надеемся, что ничего не сломается.

Будущие исследования, вероятно, сосредоточатся на автоматизации процесса верификации и валидации этих моделей. Оптимизация алгоритмов — это, конечно, важно, но куда более актуальным представляется поиск способов обойти необходимость документировать всё это безумие. Документация — это миф, созданный менеджерами, чтобы оправдать свою зарплату. Истинный прогресс заключается в создании систем, которые самодиагностируются и самовосстанавливаются, игнорируя человеческий фактор.

В конечном итоге, всё это — лишь добавление новых слоёв абстракции. Мы стремимся упростить моделирование, но каждое упрощение порождает новые сложности. И цикл повторяется. Вероятно, через десять лет появятся новые «революционные» методы, которые снова потребуют переписывания всего с нуля. И так будет всегда.

Оригинал статьи: https://arxiv.org/pdf/2602.17002.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-21 02:45