Экологическая политика в эпоху сложности: как оптимизировать решения?

Автор: Денис Аветисян

Новый подход объединяет агентное моделирование и методы статистической оптимизации для поиска эффективных стратегий в решении экологических проблем.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал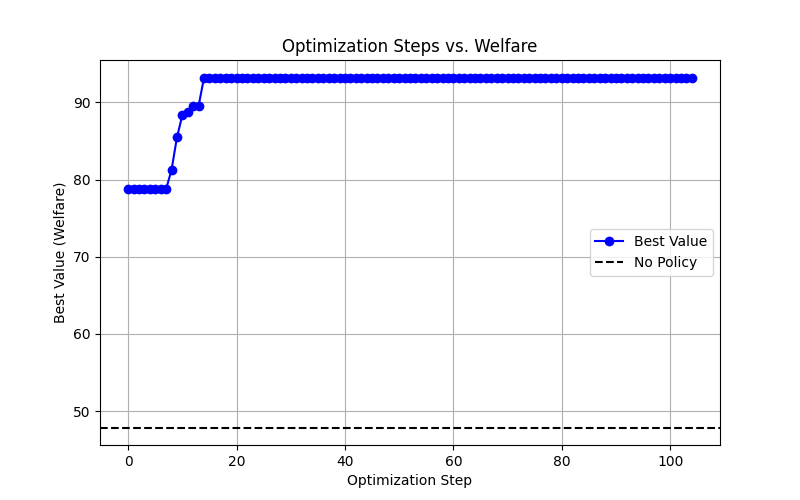

Оптимизация по методу Байеса демонстрирует улучшение целевой функции благосостояния с каждой итерацией, при этом сценарий отсутствия политики служит базовым уровнем для оценки эффективности предложенного подхода.

В статье представлен фреймворк, сочетающий байесовскую оптимизацию и гауссовские процессы для оптимизации политики в сложных агентных моделях, продемонстрированный на примере симуляции Sugarscape.

Несмотря на растущее понимание взаимосвязанных систем «человек-окружающая среда» как сложных адаптивных систем, оптимизация природоохранной политики затруднена из-за вычислительных ограничений агент-ориентированного моделирования. В данной работе, ‘Environmental policy in the context of complex systems: Statistical optimization and sensitivity analysis for ABMs’, предложен новый статистический подход, сочетающий байесовскую оптимизацию и модели Гаусса, для эффективного поиска оптимальных стратегий в сложных моделях. Показано, что разработанный фреймворк, протестированный на классической модели «Sugarscape», позволяет быстро выявлять интерпретируемые политики, превосходящие базовые методы, и проводить чувствительный анализ. Возможно ли, используя подобные методы, разработать более эффективные и устойчивые природоохранные стратегии в реальных условиях?

Понимание Сложности: Эмерджентное Поведение и Агент-Ориентированное Моделирование

Многие реальные системы, от поведения муравейника до динамики финансовых рынков, демонстрируют эмерджентное поведение — появление неожиданных, сложных закономерностей, которые невозможно предсказать, исходя из свойств отдельных компонентов. Традиционные методы моделирования, основанные на анализе средних значений и линейных зависимостей, часто оказываются неэффективными в таких случаях. Сложность заключается в том, что взаимодействие между отдельными элементами системы порождает коллективное поведение, которое не является простой суммой их индивидуальных характеристик. Например, предсказать массовую панику на фондовой бирже, основываясь только на анализе действий отдельных трейдеров, практически невозможно; требуется учитывать сложные взаимосвязи и нелинейные эффекты, возникающие в процессе взаимодействия. Понимание и моделирование эмерджентного поведения требует новых подходов, способных учитывать сложность и непредсказуемость реальных систем.

Агент-ориентированное моделирование (АОМ) представляет собой мощный инструмент для имитации взаимодействий и понимания системных результатов, особенно в тех случаях, когда традиционные аналитические методы оказываются неэффективными. Вместо упрощающих предположений о среднем поведении, АОМ рассматривает систему как совокупность автономных агентов, каждый из которых действует по своим собственным правилам и взаимодействует с другими агентами и окружающей средой. Такой подход позволяет исследовать сложные динамические процессы, возникающие из локальных взаимодействий, и наблюдать возникновение эмерджентного поведения на уровне всей системы. Благодаря возможности моделирования гетерогенности и адаптации агентов, АОМ находит применение в самых разных областях — от эпидемиологии и экономики до социологии и экологии, позволяя прогнозировать последствия различных сценариев и оценивать эффективность политических мер.

Агент-ориентированное моделирование (АОМ) рассматривает систему как совокупность автономных агентов, каждый из которых действует по собственным правилам и взаимодействует с другими. В отличие от традиционных подходов, где акцент делается на агрегированных данных и усредненных показателях, АОМ позволяет исследовать, как локальные действия отдельных агентов приводят к возникновению глобальных, эмерджентных свойств всей системы. Это особенно ценно при изучении сложных социальных, экономических и экологических процессов, где централизованное управление отсутствует или неэффективно. Благодаря возможности моделирования различных сценариев и параметров, АОМ предоставляет уникальные инструменты для оценки потенциального влияния политических мер и прогнозирования последствий различных решений, позволяя более эффективно планировать и управлять сложными системами.

Оптимизация Политик в Комплексных Системах: Байесовский Подход

Оптимизация политик в контексте агент-ориентированных моделей (АОМ) направлена на определение набора параметров, который позволяет достичь максимальных значений целевых показателей. Процесс включает в себя итеративное изменение параметров модели и оценку результирующих изменений в интересующих метриках. Цель состоит в том, чтобы найти оптимальную конфигурацию параметров, обеспечивающую наиболее благоприятный результат, определяемый заранее заданными критериями эффективности и целевыми функциями. В контексте сложных систем, характеризующихся нелинейностью и взаимодействием множества факторов, этот процесс требует систематического подхода к исследованию пространства параметров для выявления наилучших решений.

Байесовская оптимизация представляет собой последовательную стратегию проектирования, эффективно исследующую пространство параметров модели, рассматривая агент-ориентированную модель (АОМ) как «черный ящик». Данный подход позволяет достичь сходимости результатов примерно за 60 итераций, что обусловлено использованием априорных знаний и адаптивным выбором параметров для оценки. В отличие от случайного поиска или grid search, байесовская оптимизация строит вероятностную модель функции, описывающей поведение АОМ, и использует эту модель для выбора наиболее перспективных параметров для следующей итерации, минимизируя количество необходимых вычислений.

Эффективность применения байесовской оптимизации особенно проявляется в контексте агент-ориентированных моделей (АОМ), где вычисление результатов для каждого набора параметров может быть крайне ресурсоемким. В типичных сценариях, получение данных для оценки одного набора параметров в АОМ требует приблизительно 11,5 часов вычислительного времени. Такая высокая стоимость вычислений делает полный перебор параметров непрактичным, а байесовская оптимизация, используя стратегию последовательного дизайна, позволяет значительно сократить общее время, необходимое для достижения сходимости и определения оптимальных значений параметров.

Предложенный байесовский метод оптимизации последовательно улучшает целевую функцию выживаемости, демонстрируя превосходство над сценарием без применения политики (обозначен пунктирной линией).

Выявление Ключевых Драйверов Поведения Системы: Анализ Чувствительности

Анализ чувствительности позволяет установить, каким образом изменения в переменных состояния (state variables) влияют на итоговый результат агентно-ориентированной модели (ABM). Данный метод предполагает систематическое изменение значений отдельных переменных состояния и отслеживание соответствующих изменений в ключевых показателях модели. Полученные данные позволяют количественно оценить степень влияния каждой переменной на общую динамику системы, выявляя наиболее значимые факторы, определяющие ее поведение. Использование анализа чувствительности необходимо для валидации модели, определения критических параметров и снижения неопределенности при прогнозировании.

Идентификация наиболее влиятельных переменных позволяет сконцентрировать усилия по оптимизации на критически важных параметрах модели. Вместо равномерного изменения всех входных данных, что требует значительных вычислительных ресурсов и времени, можно целенаправленно варьировать только те переменные, которые оказывают наибольшее влияние на целевые показатели. Такой подход значительно повышает эффективность процесса оптимизации, снижает затраты на вычисления и позволяет быстрее достичь оптимальных значений параметров, обеспечивая более точную и надежную калибровку модели агентного моделирования.

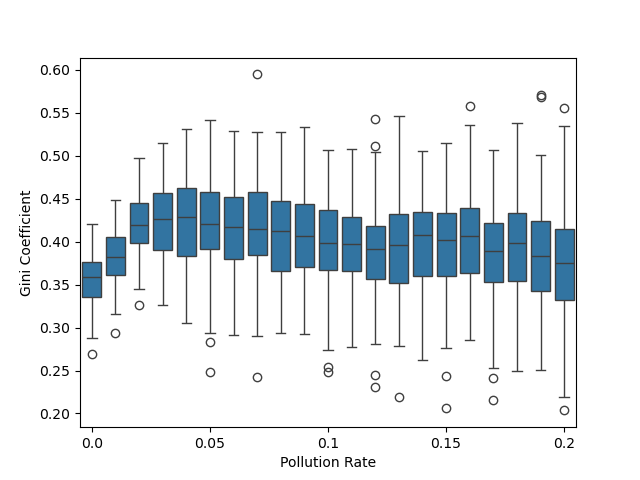
Результаты анализа чувствительности продемонстрировали статистически значимую зависимость (p < 0.05) оптимальных вариантов политик от таких переменных состояния, как уровень загрязнения и метаболизм агентов. Это указывает на то, что незначительные изменения в этих переменных могут существенно повлиять на эффективность выбранной политики. Выявление этой зависимости позволяет повысить эффективность и устойчивость стратегии оптимизации, поскольку фокус может быть направлен на наиболее влияющие параметры, а также позволяет более точно прогнозировать последствия различных политических решений в условиях изменяющейся среды.

Байесовская оптимизация последовательно улучшает коэффициент Джини, демонстрируя превосходство над сценарием без политики, что подтверждается графиком зависимости коэффициента Джини от числа итераций.

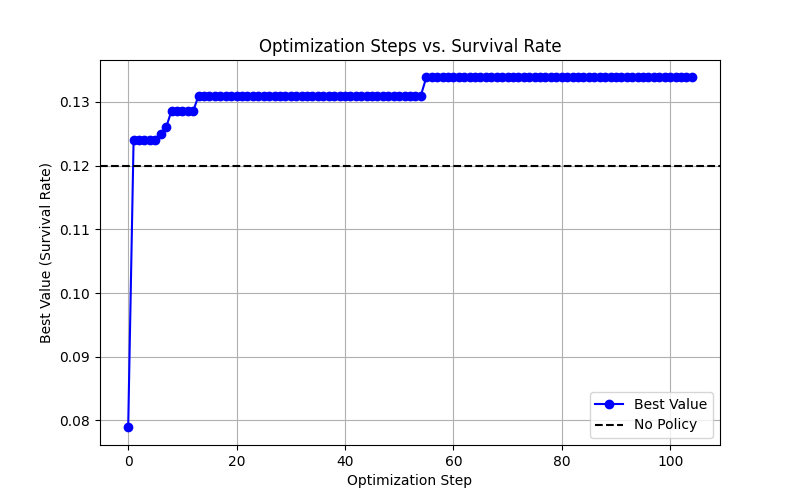
Оценка Влияния Политик на Результаты Системы: Моделирование Sugarscape

В рамках модели Sugarscape, применение таких политик, как ограничение производства (ProductionCap) и налог на торговлю (TradeTax), оказывает существенное влияние на благосостояние (Welfare) и выживаемость (SurvivalRate) агентов. Моделирование показывает, что даже относительно простые регуляторные меры способны кардинально изменить распределение ресурсов и, как следствие, уровень жизни отдельных агентов. В частности, политика ограничения производства может снизить общее количество доступных ресурсов, но при этом повысить их стоимость, что положительно скажется на благосостоянии тех, кто сохранит доступ к ним. Налог на торговлю, в свою очередь, перераспределяет ресурсы, потенциально уменьшая разрыв между наиболее и наименее обеспеченными агентами, хотя и может оказывать негативное влияние на общую экономическую активность. Анализ чувствительности показывает, что эффект от этих политик зависит от множества факторов, включая начальное распределение ресурсов и параметры моделирования, что подчеркивает необходимость тщательного анализа при разработке и внедрении реальных политических мер.

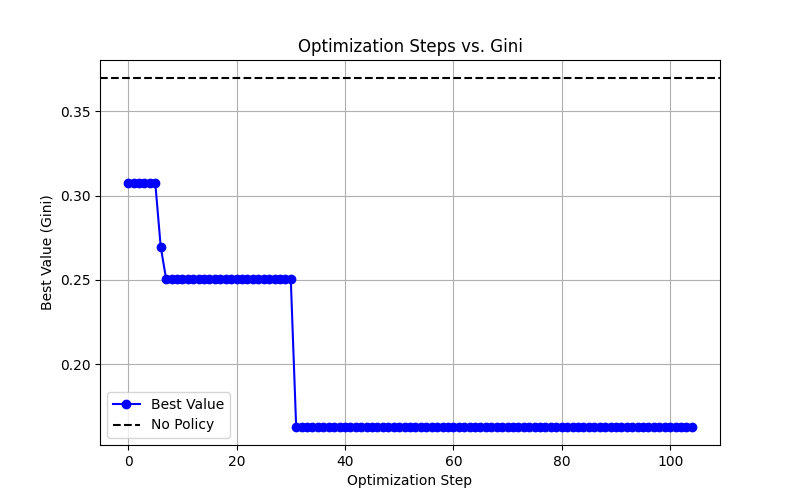
В рамках оптимизации политических мер, направленных на улучшение социально-экономических показателей, особое внимание уделяется не только максимизации общих показателей благосостояния и выживаемости агентов, но и обеспечению более справедливого распределения ресурсов. Использование коэффициента Джини, как индикатора неравенства, позволяет оценить, насколько равномерно распределяются блага между всеми участниками системы. Современные методы оптимизации, в частности, байесовская оптимизация, нацелены на поиск таких политик, которые одновременно повышают общий уровень благосостояния и снижают неравенство, выраженное коэффициентом Джини. Такой подход позволяет создавать более устойчивые и справедливые системы, учитывающие не только эффективность, но и социальную справедливость.

В ходе моделирования на базе Sugarscape, разработанные политические меры, такие как ограничение производства и налогообложение торговли, последовательно демонстрировали превосходство над сценарием их отсутствия. Применение метода байесовской оптимизации позволило добиться 2,5-кратного снижения коэффициента Джини, отражающего уровень неравенства, по сравнению со случайным подбором параметров. Важно отметить, что модель учитывает не только прямые показатели благосостояния и выживаемости агентов, но и негативные внешние эффекты, в частности, загрязнение окружающей среды, что значительно повышает реалистичность и сложность оценки эффективности предлагаемых политических решений.

Распределение коэффициентов Джини (рассчитанных на основе благосостояния агентов) по 100 моделям, каждая из которых длилась 500 шагов в модели торговли Sugarscape, демонстрирует степень неравенства в распределении ресурсов.

К Реалистичным Симуляциям и Устойчивым Политикам: Учет Гетерогенности и Метаболизма

Неоднородность агентов и их начальное оснащение играют ключевую роль в формировании поведения отдельных участников и общей динамики системы. Исследования показывают, что даже незначительные различия в характеристиках агентов — будь то скорость обучения, предпочтения или доступные ресурсы — могут приводить к существенным отклонениям в их стратегиях и, как следствие, к непредсказуемым изменениям в функционировании всей системы. Начальное оснащение, определяющее стартовые условия каждого агента, оказывает особенно сильное влияние, формируя траектории развития и определяя возможности для адаптации. Таким образом, учет гетерогенности и начальных условий необходим для создания реалистичных моделей и разработки эффективных политик, способных учитывать разнообразие агентов и обеспечивать устойчивость системы в различных сценариях.

Включение параметра скорости метаболизма в моделирование значительно повышает реалистичность симуляций, поскольку учитывает фундаментальные процессы потребления ресурсов и давления отбора. Этот фактор определяет, насколько быстро агенты используют энергию и другие необходимые ресурсы для поддержания жизнедеятельности и размножения. Агенты с более высокой скоростью метаболизма нуждаются в большем количестве ресурсов, что создает конкуренцию и влияет на их способность к выживанию, особенно в условиях ограниченной доступности. Учет скорости метаболизма позволяет более точно отразить динамику популяций и спрогнозировать, как различные стратегии поведения будут влиять на их устойчивость и адаптацию к меняющимся условиям окружающей среды. Таким образом, моделирование с учетом скорости метаболизма позволяет получить более правдоподобные результаты и разработать более эффективные стратегии управления ресурсами и сохранения биоразнообразия.

Интеграция факторов, таких как гетерогенность агентов, начальные условия и скорость метаболизма, в оптимизационные модели позволяет создавать более устойчивые и справедливые стратегии. Традиционные подходы часто игнорируют разнообразие внутри популяции и неравномерное распределение ресурсов, что приводит к политикам, не учитывающим потребности различных групп. Включение этих аспектов в процесс оптимизации позволяет учитывать индивидуальные особенности каждого агента и обеспечивать, чтобы разработанные стратегии были эффективны и справедливы для всех, независимо от их начальных условий или скорости потребления ресурсов. Это особенно важно в сложных системах, где небольшие различия в начальных условиях могут привести к значительным различиям в результатах, и где устойчивость системы зависит от способности адаптироваться к разнообразию и неравенству.

Динамика выживаемости демонстрирует изменения в проценте особей, сохраняющих жизнеспособность с течением времени.

Исследование демонстрирует, что оптимизация политик в сложных системах требует не слепой веры в модели, а постоянной проверки и уточнения. Авторы предлагают методологию, сочетающую байесовскую оптимизацию и гауссовские процессы, позволяющую эффективно исследовать пространство возможных решений. Этот подход особенно важен, учитывая, что агент-базированное моделирование, как показано на примере Sugarscape, часто сталкивается с проблемой высокой вычислительной сложности. В связи с этим, уместно вспомнить слова Генри Дэвида Торо: «Не ищите правду в убеждениях, а ищите её в исследовании». Ведь гипотеза — это не догма, а приглашение к сомнению, а истина рождается не из одной модели, а из последовательности проверок, ошибок и критического анализа.

Что дальше?

Представленный подход, сочетающий байесовскую оптимизацию и гауссовские процессы для настройки политики в моделях, основанных на агентах, демонстрирует определенный прогресс, однако не стоит переоценивать его значимость. Данные — не цель, а зеркало человеческих ошибок. Эффективность алгоритмов оптимизации в искусственной среде Sugarscape не гарантирует ее сохранения в более реалистичных, многосложных системах, где взаимодействие агентов подвержено непредсказуемым факторам и нелинейным зависимостям. Поиск оптимальной политики, даже в рамках упрощенной модели, — задача скорее методологическая, чем практическая.

Необходимо признать, что всё, что нельзя измерить, всё равно влияет — просто это труднее моделировать. Дальнейшие исследования должны быть направлены на учет неопределенностей, связанных с неполнотой данных и несовершенством моделей. Интеграция методов машинного обучения с традиционными подходами к моделированию сложных систем представляется перспективной, но требует критической оценки и постоянной проверки. Проблема не в создании более сложных моделей, а в разработке инструментов для верификации и валидации этих моделей.

Особое внимание следует уделить проблеме масштабируемости. Эффективность байесовской оптимизации снижается с увеличением числа параметров и агентов. Разработка алгоритмов, способных эффективно справляться с задачами высокой размерности, является ключевым вызовом для дальнейших исследований. В конечном счете, ценность модели определяется не ее математической изяществом, а ее способностью пролить свет на реальные проблемы и предложить практически значимые решения.

Оригинал статьи: https://arxiv.org/pdf/2602.17079.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-20 23:28