Финансовые временные ряды: разделение на скорости

Автор: Денис Аветисян

Новый метод позволяет разделить финансовые данные на компоненты, различающиеся по временным масштабам, открывая возможности для анализа дрейфа параметров и оценки рисков.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал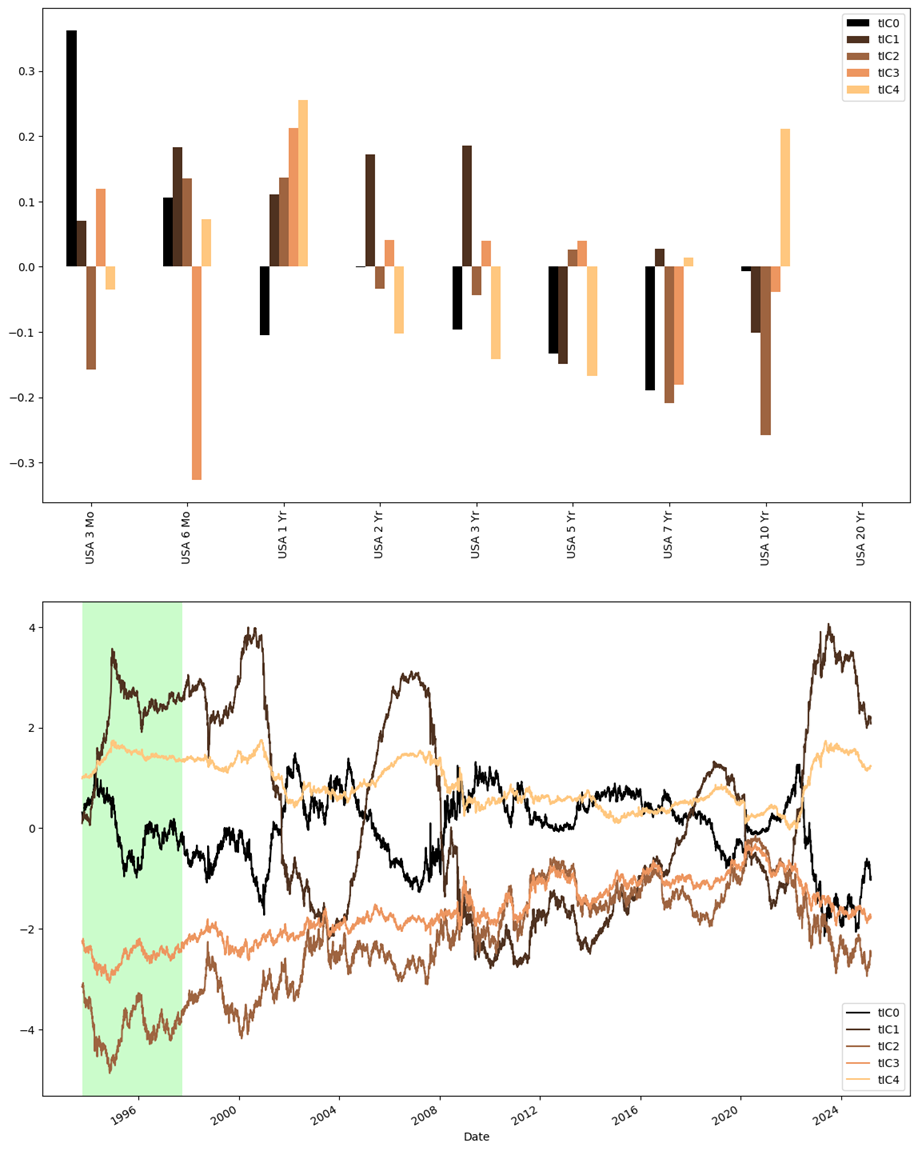

На временном отрезке с 1994 по 2025 год, анализ динамики американских казначейских облигаций выявил закономерность: извлечение наиболее медленных компонентов, нормализованное к единой суммарной позиции, демонстрирует преемственность тенденций, начавшихся в период с 1994 по 1998 год (обозначенных зелёным цветом) и продолжившихся в последующие годы (обозначенных белым цветом).

В статье представлена методика разделения временных рядов на основе обобщенной задачи на собственные значения, позволяющая выявить стабильные временные масштабы и оценить параметры дрейфа, возврат к среднему и стабильность экстремальных рисков.

Финансовые временные ряды часто демонстрируют сложное поведение, обусловленное взаимодействием процессов, протекающих в различных временных масштабах. В работе ‘Fast Times, Slow Times: Timescale Separation in Financial Timeseries Data’ предложен метод разделения этих процессов на основе критериев стационарности дисперсии и хвостов, сформулированный в виде обобщенной задачи на собственные значения. Данный подход позволяет идентифицировать медленные и быстрые компоненты в доходностях активов и ценах, что открывает возможности для анализа смещения параметров, возврат к среднему и управления рисками в «хвостах» распределений. Позволит ли более глубокое понимание этих временных масштабов повысить стабильность и эффективность финансовых стратегий?

Раскрытие Скрытых Ритмов: Необходимость Разделения Временных Масштабов

Традиционные финансовые модели, как правило, опираются на предположение о статических взаимосвязях между различными факторами, влияющими на рынки. Однако, реальные финансовые системы представляют собой сложные, многоуровневые системы, где процессы происходят в разных временных масштабах. Например, высокочастотные сделки, совершаемые за доли секунды, оказывают мгновенное влияние на цену актива, в то время как долгосрочные фундаментальные факторы, такие как экономический рост или изменения в процентных ставках, формируют тренды на протяжении месяцев или лет. Игнорирование этой многомасштабности приводит к упрощенным моделям, не способным адекватно отразить динамику рынков и, как следствие, к неточным прогнозам и повышенным рискам. Поэтому, для более реалистичного моделирования необходимо учитывать взаимодействие между быстрыми и медленными процессами, происходящими в финансовых системах.

В финансовых системах, подобно многим явлениям в физике, наблюдается сложная иерархия процессов, протекающих в различных временных масштабах. Для адекватного анализа и моделирования необходимо разделять эти быстрые и медленные динамики, выявляя скрытые структуры и взаимосвязи. Такой подход позволяет отделить краткосрочные колебания, обусловленные, например, спекулятивными операциями, от долгосрочных трендов, определяемых фундаментальными факторами. Эффективные методы разделения временных масштабов, такие как вейвлет-анализ или анализ спектральной плотности, предоставляют инструменты для фильтрации шума, выявления доминирующих частот и прогнозирования будущих изменений. В конечном итоге, способность разделять динамику в различных масштабах является ключевым фактором для построения более точных и надежных финансовых моделей, способных адаптироваться к сложной и изменчивой рыночной среде.

Понимание временных масштабов, на которых протекают финансовые процессы, имеет решающее значение для построения адекватных моделей поведения активов и эффективного управления рисками. Рынки характеризуются взаимодействием быстрых и медленных процессов — от высокочастотных торгов до долгосрочных инвестиционных стратегий. Игнорирование этой многомасштабности приводит к упрощенным моделям, не способным отразить реальную динамику и предсказать будущие изменения. Точное разделение этих временных масштабов позволяет выявить скрытые взаимосвязи, оценить чувствительность активов к различным факторам и, в конечном итоге, разработать более надежные стратегии для минимизации потенциальных потерь и максимизации прибыли. Анализ данных на разных временных горизонтах предоставляет возможность более глубокого понимания рыночных тенденций и позволяет принимать обоснованные инвестиционные решения.

Анализ факторного ETF показывает, что извлечение самых медленных компонентов в период 2021-2022 годов (зеленый фон) продолжилось и в 2022-2025 годах (белый фон), при этом веса были нормализованы до единой общей экспозиции.

Временная Динамика: Метод Независимых Компонент (tICA)

Метод временного независимого компонентного анализа (tICA) представляет собой эффективный инструмент для разложения финансовых временных рядов на компоненты, функционирующие в различных временных масштабах. В основе tICA лежит предположение о том, что сложные финансовые данные можно представить в виде суммы независимых сигналов, каждый из которых характеризуется своей собственной скоростью изменения. Разложение позволяет выделить доминирующие динамики, скрытые в исходных данных, и отделить краткосрочные колебания от долгосрочных трендов. Это достигается путем поиска линейных комбинаций исходных временных рядов, которые максимально статистически независимы и демонстрируют минимальную скорость изменения во времени. Результатом является набор компонентов, каждый из которых отражает динамику определенного временного масштаба, что позволяет проводить более детальный анализ и прогнозирование финансовых данных.

Метод tICA основан на решении обобщенной задачи на собственные значения (Generalized Eigenvalue Problem) для выявления компонент временных рядов, характеризующихся минимальным изменением дисперсии во времени. Решение этой задачи позволяет идентифицировать компоненты, отражающие доминирующие динамические процессы, путем минимизации дрейфа дисперсии. В математической постановке, искомые компоненты являются собственными векторами ковариационной матрицы, построенной на основе данных временного ряда, а соответствующие собственные значения характеризуют величину дрейфа дисперсии. Компоненты с наименьшими собственными значениями рассматриваются как компоненты с минимальным дрейфом, что указывает на их стабильность и доминирующую роль в динамике системы. $\mathbf{v} = \mathbf{W}^{-1} \mathbf{V}$ , где $\mathbf{v}$ — собственные векторы, $\mathbf{W}$ — матрица ковариаций, а $\mathbf{V}$ — матрица, определяющая динамику.

Линейная и нелинейная версии tICA расширяют базовую методологию, предлагая различные подходы к разложению временных рядов. Линейный tICA использует линейные модели для идентификации независимых компонент, в то время как нелинейный tICA применяет нелинейные преобразования, позволяющие выявлять более сложные зависимости во временных данных. В результате применения этих двух версий получаются качественно различные временные ряды, отражающие разную степень учета нелинейных эффектов и, следовательно, различные представления о динамике исходного процесса. Различия в полученных результатах позволяют более точно интерпретировать поведение финансовых данных и выделять компоненты, недоступные при использовании только линейных методов.

Анализ валют G10 показывает, что выделение наиболее медленных компонентов в период с 2006 по 2010 год (зеленый фон) и их последующее продление до 2025 года (белый фон) при масштабировании суммарной экспозиции позволяет выявить устойчивые тенденции.

За пределами Дисперсии: Выявление Рисков в Хвостах Распределений

Анализ временных масштабов дисперсии, определяемых ковариационной матрицей, предоставляет информацию о стабильности доходности активов. Ковариационная матрица описывает взаимосвязь между различными активами и их волатильность. Извлекая собственные значения и собственные векторы из этой матрицы, можно определить доминирующие временные масштабы, на которых происходят изменения доходности. Более крупные собственные значения соответствуют более быстрым масштабам, в то время как меньшие собственные значения указывают на более медленные, долгосрочные тренды. Анализ этих масштабов позволяет оценить, насколько стабильны текущие закономерности доходности и выявить потенциальные изменения в динамике активов. Например, снижение доминирующих временных масштабов может указывать на возрастающую волатильность и неустойчивость доходности.

Для адекватной оценки экстремальных событий, традиционный анализ дисперсии необходимо расширять до анализа “хвостовых” временных масштабов. Это предполагает переход от рассмотрения только второго момента (дисперсии) к анализу высших моментов распределения, таких как асимметрия и эксцесс. Стабильность “хвостового” поведения, то есть устойчивость формы распределения в области экстремальных значений, становится ключевым параметром. Нестабильность на этих масштабах указывает на повышенную вероятность возникновения событий, значительно отклоняющихся от ожидаемых, и, следовательно, на наличие $tail risk$ . Оценка этих моментов и их стабильности позволяет более точно моделировать вероятность и потенциальные последствия экстремальных рыночных колебаний.

Метод итераций с фиксированной точкой (Fixed Point Iteration) является ключевым инструментом в сочетании с временной независимой компонент-анализом (tICA) для определения параметров, характеризующих поведение активов в «хвостах» распределения. tICA позволяет выделить временные масштабы, соответствующие экстремальным событиям, а итерации с фиксированной точкой используются для решения уравнений, возникающих при анализе этих масштабов. Этот подход позволяет выявить компоненты, определяющие стабильность и вероятность возникновения событий в «хвостах» распределения, что критически важно для оценки и управления рисками, связанными с экстремальными рыночными условиями. Результатом является возможность количественно оценить источники Tail Risk, определяя вклад различных факторов в вероятность возникновения крупных потерь.

Эмпирическое Подтверждение: Устойчивость в Разных Классах Активов

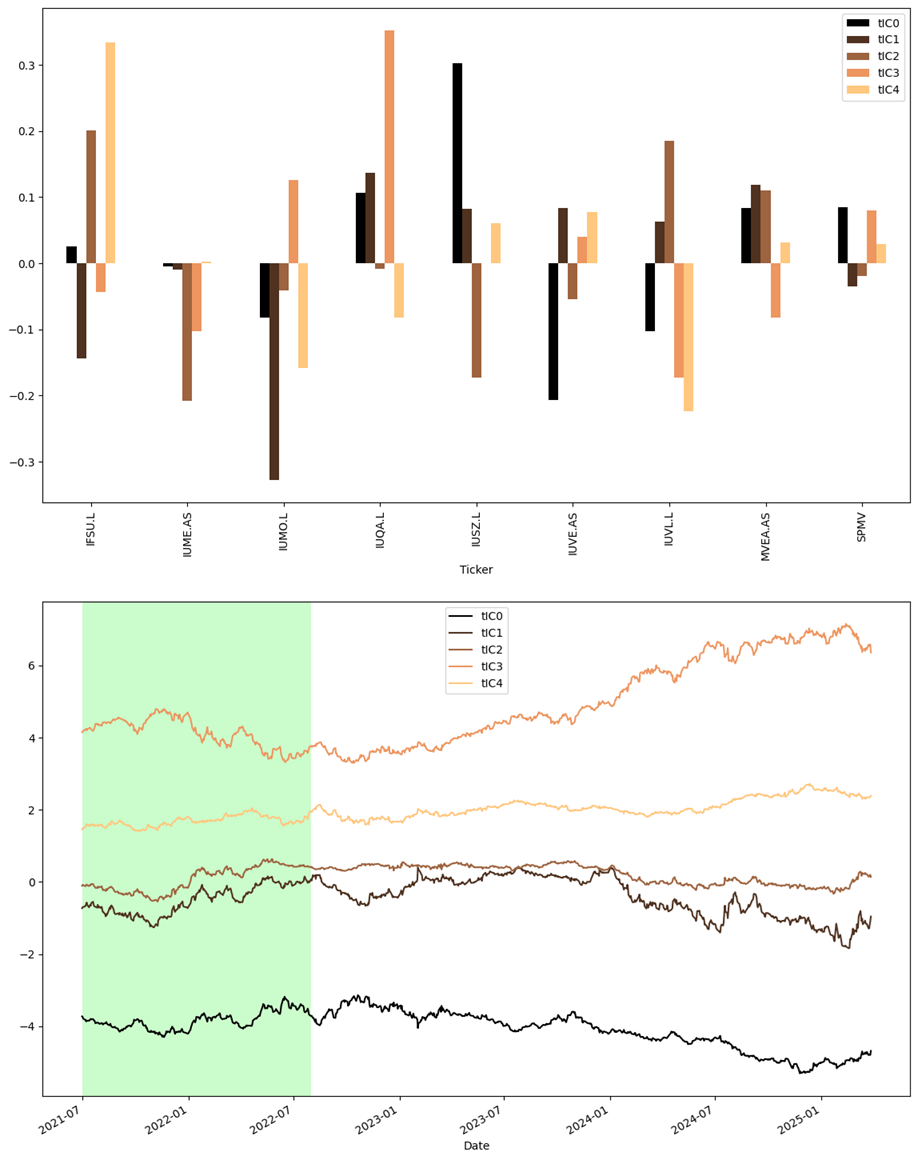
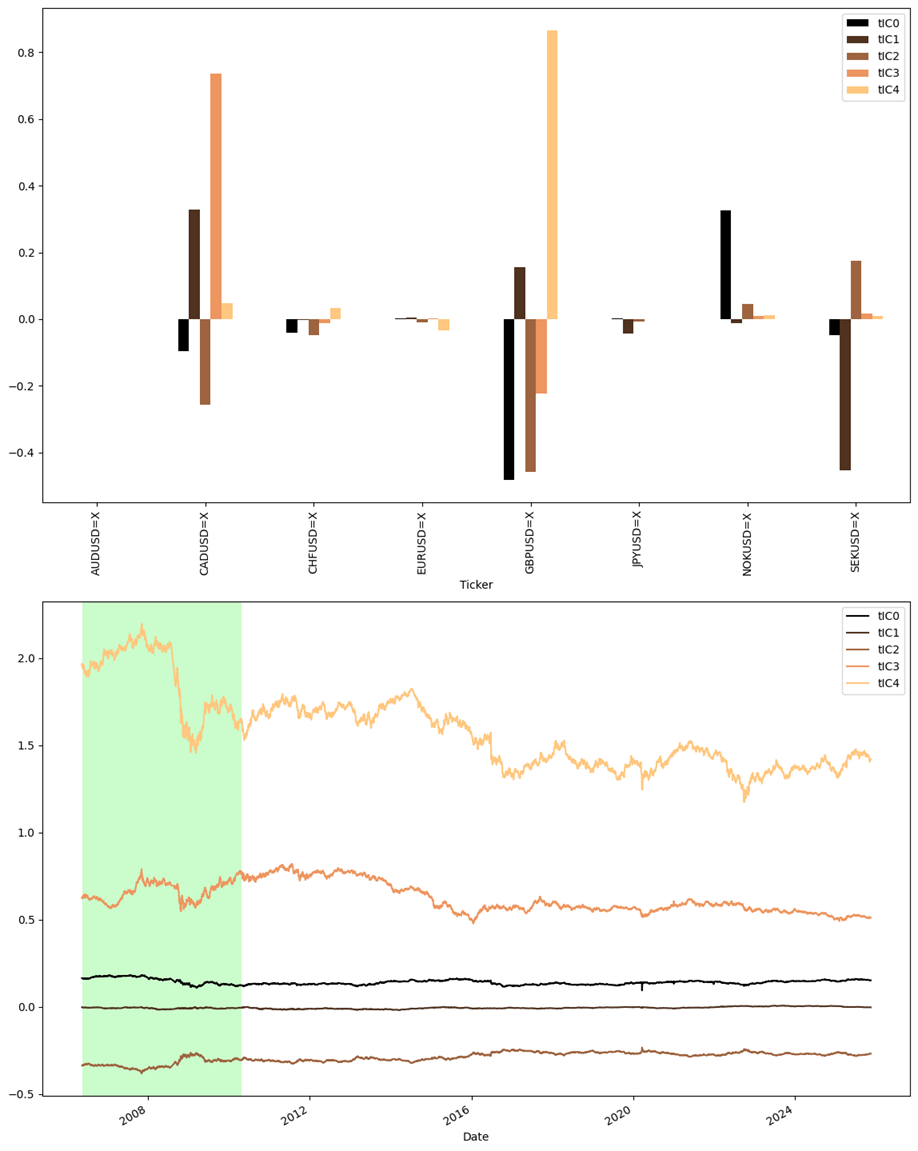
Метод временных независимых компонент (tICA) был успешно применен к широкому спектру финансовых инструментов, включая валюты G10, казначейские облигации США и факторные ETF. Исследование охватывает значительный период времени — с 1994 по 2025 год для казначейских облигаций, с 2006 по 2025 год для валют G10 и с 2021 по 2025 год для факторных ETF — демонстрируя адаптивность подхода к различным классам активов и временным горизонтам. Данная универсальность подчеркивает потенциал tICA как инструмента для выявления общих динамических характеристик в сложных финансовых системах, вне зависимости от конкретного типа анализируемого актива.

Анализ временных характеристик различных финансовых активов — валют G10, казначейских облигаций США и факторных ETF — выявил поразительное единство в их динамике. Исследование показало, что, несмотря на различия в природе этих инструментов, они демонстрируют схожие временные масштабы, что указывает на наличие общих фундаментальных факторов, определяющих их поведение. Этот результат предполагает, что за кажущимся разнообразием финансовых рынков скрываются общие, лежащие в основе закономерности, определяющие долгосрочные тенденции и цикличность. Выявление этих общих динамических характеристик открывает возможности для более глубокого понимания взаимосвязей между активами и разработки более эффективных стратегий управления рисками и инвестирования.

Анализ временных масштабов, выявленных при помощи tICA, демонстрирует удивительную устойчивость к изменениям рыночной конъюнктуры. В ходе исследования установлено, что эти масштабы сохраняют свою структуру и не подвергаются заметным искажениям при переходе от исторических данных к новым, ранее не использованным периодам. Более того, после значимых событий, таких как финансовый кризис 2008-2010 годов или геополитические потрясения 2023 года, компоненты, определяющие эти масштабы, закономерно возвращаются к своим исходным, медленным значениям. Данная особенность подчеркивает фундаментальную природу выявленных динамик и свидетельствует о способности метода tICA выявлять устойчивые закономерности в финансовых рынках, не зависящие от краткосрочных колебаний и внешних шоков.

Исследование временных рядов финансов подобно попытке удержать ускользающий туман. Авторы предлагают разделить этот туман на слои по скорости изменения, выявить скрытые ритмы. Этот подход к разделению временных масштабов, позволяющий анализировать стабильность параметров и выявлять дрейф, вызывает странное дежавю. Кажется, будто они пытаются приручить хаос, заставив его плясать под предсказуемые барабаны. Бертранд Рассел однажды заметил: «Страх — это больше, чем предвидение бедствия; это предчувствие, что бедствие неизбежно». В данном случае, «бедствие» — это нестабильность рынка, а предложенный метод — попытка унять это предчувствие, хотя и ясно, что любые модели рано или поздно столкнутся с реальностью.

Куда же дальше?

Предложенный подход к разделению финансовых временных рядов по временным масштабам, безусловно, дарит иллюзию контроля над хаосом. Он позволяет выделить компоненты, демонстрирующие стабильность во времени, что, конечно, приятно для глаза. Однако, стоит помнить: стабильность — это всего лишь затишье перед новой бурей. Выделенные масштабы времени, как ни парадоксально, лишь подтверждают, что будущее всегда немного отличается от прошлого, а все модели — это заклинания, работающие до первой реальной сделки.

Наиболее сложным представляется вопрос о природе “дрифта параметров”. Обнаружение этого дрифта — не более чем констатация факта, но объяснить его причины — задача куда более трудная. Данные не врут, они просто помнят избирательно. Будущие исследования должны быть направлены на понимание механизмов, порождающих этот дрифт, и, возможно, на создание моделей, способных предсказывать его направление, хотя сама идея предсказания — это, конечно, чистая вера.

Особый интерес представляет возможность применения данного подхода к анализу не только финансовых, но и других сложных систем, где наблюдается многомасштабность. Однако, следует помнить: любая метрика — это всего лишь форма самоуспокоения. Настоящее понимание приходит не через цифры, а через осознание пределов нашего знания.

Оригинал статьи: https://arxiv.org/pdf/2601.11201.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-19 18:45