Физика финансов: как законы Ньютона улучшают алгоритмы машинного обучения

Автор: Денис Аветисян

Новое исследование демонстрирует, что использование принципов физики в алгоритмах глубокого обучения с подкреплением позволяет повысить стабильность и прибыльность инвестиционных стратегий.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Предлагается структура обучения с подкреплением, интегрирующая физические ограничения для оптимизации портфеля активов, где динамика портфеля описывается уравнением [latex]P\_{t}=P\_{t-1}(\mathbf{w}\_{t-1}^{\to p}\mathbf{y}\_{t})\mu\_{t}[/latex], учитывающим веса активов [latex]\mathbf{w}\_{t}[/latex], относительные цены [latex]\mathbf{y}\_{t}[/latex] и транзакционные издержки [latex]\mu\_{t}=1-c\,\mathrm{TO}\_{t}[/latex], при этом закон Ньютона [latex]F=ma[/latex] внедряется через функцию потерь [latex]L\_{\text{phys}}=\frac{1}{B}\sum\_{i}(\hat{\alpha}\_{t,i}-\alpha\_{t,i})^{2}[/latex], связывающую ускорение [latex]\alpha\_{t}=\Delta v\_{t}/\Delta t[/latex] с весами активов [latex]\hat{\alpha}\_{t}=a\_{t}/m[/latex]. — Предлагается структура обучения с подкреплением, интегрирующая физические ограничения для оптимизации портфеля активов, где динамика портфеля описывается уравнением $P\_{t}=P\_{t-1}(\mathbf{w}\_{t-1}^{\to p}\mathbf{y}\_{t})\mu\_{t}$ , учитывающим веса активов $\mathbf{w}\_{t}$ , относительные цены $\mathbf{y}\_{t}$ и транзакционные издержки $\mu\_{t}=1-c\,\mathrm{TO}\_{t}$ , при этом закон Ньютона $F=ma$ внедряется через функцию потерь $L\_{\text{phys}}=\frac{1}{B}\sum\_{i}(\hat{\alpha}\_{t,i}-\alpha\_{t,i})^{2}$ , связывающую ускорение $\alpha\_{t}=\Delta v\_{t}/\Delta t$ с весами активов $\hat{\alpha}\_{t}=a\_{t}/m$ .

В статье представлена методика интеграции физически обоснованной регуляризации, основанной на законах Ньютона, в алгоритмы глубокого обучения с подкреплением для оптимизации портфеля и управления рисками в финансовых рынках.

Несмотря на успехи глубокого обучения с подкреплением в задачах финансовой торговли, алгоритмы часто демонстрируют нестабильность и низкую обобщающую способность в условиях волатильных рынков. В данной работе, озаглавленной ‘The Enhanced Physics-Informed Kolmogorov-Arnold Networks: Applications of Newton’s Laws in Financial Deep Reinforcement Learning (RL) Algorithms’, предлагается новый подход к оптимизации портфеля, основанный на интеграции сетей Колмогорова-Арнольда с физически обоснованной регуляризацией, имитирующей принципы ньютоновской динамики. Результаты экспериментов на рынках Китая, Вьетнама и США подтверждают, что предложенный метод обеспечивает более высокую доходность, улучшенные показатели Шарпа и Кальмара, а также снижает риски просадок. Сможет ли данный подход стать основой для разработки более устойчивых и эффективных алгоритмов автоматизированной торговли в будущем?

Элегантность в Оптимизации: Преодолевая Статичные Модели

Традиционные методы распределения активов зачастую оказываются неэффективными в условиях реальных рынков, поскольку опираются на статические предположения, игнорирующие динамические изменения волатильности и транзакционных издержек. Эти подходы, как правило, предполагают стабильность рыночных параметров, что не соответствует действительности, где колебания цен и затраты на совершение сделок постоянно меняются. В результате, портфели, сформированные на основе таких упрощенных моделей, могут оказаться недостаточно гибкими для адаптации к новым условиям, приводя к упущенной выгоде и повышенному риску. Игнорирование этих факторов может существенно снизить потенциальную доходность и увеличить подверженность неблагоприятным рыночным колебаниям, особенно в периоды повышенной неопределенности и турбулентности.

Эффективное управление инвестиционным портфелем в современных условиях требует от методик способности адаптироваться к непрерывным изменениям рыночной конъюнктуры и учитывать реалистичные ограничения. Традиционные подходы часто оказываются неэффективными из-за их неспособности отразить динамику волатильности, издержки транзакций и прочие факторы, влияющие на доходность. Современные алгоритмы оптимизации стремятся к созданию гибких стратегий, способных оперативно реагировать на новые данные и корректировать структуру портфеля, минимизируя риски и максимизируя потенциальную прибыль. Особое внимание уделяется учету инерционности рынка — тенденции активов сохранять предыдущее направление движения — и затратам, связанным с покупкой и продажей активов, поскольку их игнорирование может существенно снизить итоговый результат инвестирования.

Игнорирование инерции рынка и транзакционных издержек способно существенно снизить потенциальную доходность портфеля и повысить подверженность рискам. В реальности, рынки не реагируют мгновенно на изменения, проявляя определенную инерцию, а каждая сделка сопряжена с затратами — комиссиями, спредами, налоговыми последствиями. Не учитывая эти факторы при ребалансировке портфеля, инвестор рискует совершать слишком частые и незначительные сделки, «съедая» прибыль на комиссиях, или, наоборот, упуская возможности, связанные с медленным реагированием рынка. Оптимизация портфеля должна включать в себя анализ этих издержек и учет инерции рынка для достижения более стабильных и высоких результатов, а также минимизации рисков, связанных с волатильностью и непредсказуемостью рыночной конъюнктуры.

В процессе обучения алгоритм A2C (для американского рынка) динамически изменяет веса портфеля для оптимизации стратегии.

Глубокое Обучение с Подкреплением: Интеллектуальные Агенты в Действии

Глубокое обучение с подкреплением (DRL) представляет собой методологию обучения агентов принятию последовательных решений в сложных средах, превосходящую традиционные системы, основанные на жестких правилах. В отличие от экспертных систем, требующих ручного определения всех возможных сценариев и соответствующих действий, DRL позволяет агенту самостоятельно изучать оптимальную стратегию поведения путем взаимодействия со средой и максимизации суммарного вознаграждения. Это достигается за счет использования глубоких нейронных сетей для аппроксимации функции ценности или политики, что позволяет эффективно обрабатывать большие объемы данных и обобщать полученный опыт на новые, ранее не встречавшиеся ситуации. Таким образом, DRL обеспечивает адаптивность и гибкость, недоступные для систем с фиксированным набором правил.

Алгоритмы, такие как DDPG (Deep Deterministic Policy Gradient), PPO (Proximal Policy Optimization), TD3 (Twin Delayed DDPG) и A2C (Advantage Actor-Critic), используют глубокие нейронные сети для аппроксимации оптимальных политик управления агентом. В основе их работы лежит обучение с подкреплением, где нейронная сеть выступает в роли функции, отображающей состояние среды в действие. Эти алгоритмы стремятся максимизировать кумулятивную награду, получаемую агентом в процессе взаимодействия со средой. Различные архитектуры и функции потерь, используемые в этих алгоритмах, позволяют эффективно решать задачи с непрерывными пространствами действий и высокой размерностью состояний, превосходя традиционные методы обучения с подкреплением.

Стандартные алгоритмы глубокого обучения с подкреплением (DRL) часто требуют значительных объемов данных для эффективной тренировки, что может быть проблемой при ограниченном доступе к данным или высокой стоимости их сбора. Кроме того, такие подходы демонстрируют недостаточную устойчивость к непредсказуемым изменениям в среде, таким как внезапные колебания рынка или появление новых факторов, не учтенных в процессе обучения. Это связано с тем, что обученная политика оптимизирована под конкретное распределение данных, и её производительность может существенно снижаться при отклонении от этого распределения, требуя повторной тренировки или применения методов адаптации к изменяющимся условиям.

В ходе тестирования на вьетнамском рынке агенты обучения с подкреплением, использующие физически обоснованные модели, демонстрируют повышенную стабильность и превосходящую суммарную доходность по сравнению с моделями, не учитывающими физические принципы.

Физически Обоснованные Сети: Сближение Теории и Практики

Интеграция физических принципов, таких как второй закон Ньютона, в структуры глубокого обучения с подкреплением (DRL) посредством Physics-Informed Neural Networks (PINN) выполняет функцию регуляризации. Этот подход позволяет ограничивать пространство поиска решений, направляя алгоритм к результатам, согласующимся с установленными рыночными закономерностями. Введение физических ограничений в процесс обучения способствует повышению стабильности и обобщающей способности модели, особенно в задачах, где динамика системы описывается известными физическими законами. По сути, PINN используют информацию о производных и взаимосвязях между переменными, чтобы штрафовать решения, которые физически неправдоподобны, тем самым улучшая соответствие модели реальным рыночным процессам.

Комбинирование сетей, основанных на физических принципах (Physics-Informed Neural Networks, PINN), с сетями Колмогорова-Арнольда (Kolmogorov-Arnold Networks) позволяет улучшить подход к моделированию за счет использования сплайн-аппроксимации. Сплайны обеспечивают более гладкую и эффективную аппроксимацию функций, что приводит к снижению вычислительных затрат и повышению скорости обучения модели. Использование сплайнов также улучшает интерпретируемость модели, поскольку сплайн-функции легче анализировать и понимать, чем сложные нелинейные функции, используемые в стандартных нейронных сетях. В результате, данная комбинация позволяет создавать более эффективные и понятные модели для решения сложных задач, требующих высокой точности и скорости вычислений.

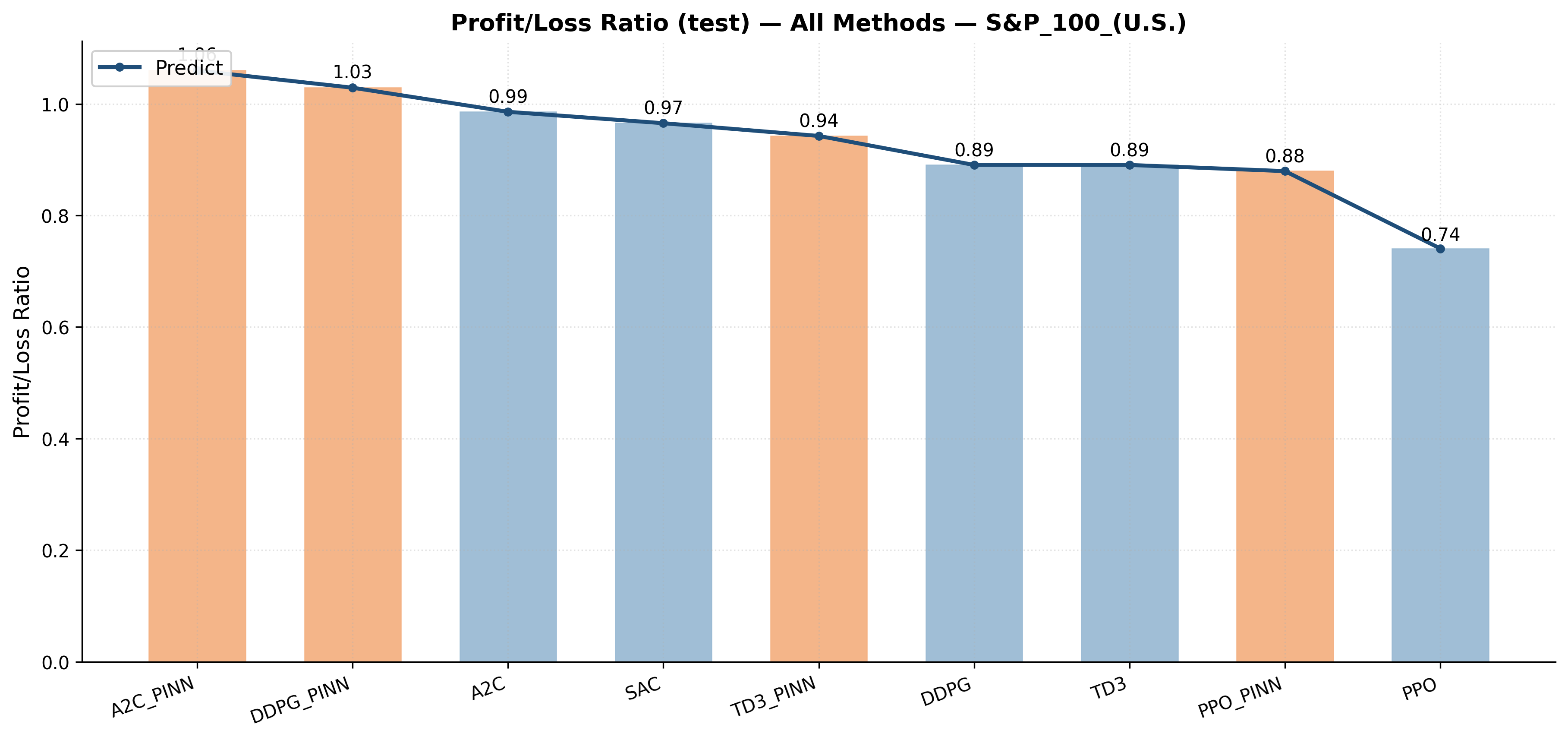
Интеграция физически обоснованных нейронных сетей (PINN) с алгоритмами обучения с подкреплением, такими как DDPG, PPO, TD3 и A2C, демонстрирует улучшение результатов в задачах динамической оптимизации портфеля. В частности, использование A2C_PINN на американском рынке позволило достичь коэффициента Шарпа $1.54$ , что значительно превосходит стандартное значение коэффициента Шарпа для A2C, составляющее $0.36$ . Данные результаты подтверждают эффективность подхода, основанного на включении физических принципов в процесс обучения, для повышения производительности алгоритмов в задачах управления инвестиционным портфелем.

На тестовом наборе S&P 100 (США) методы, использующие физические принципы, демонстрируют превосходную эффективность с учетом риска.

Измерение Успеха: Выходя за Рамки Простой Доходности

Оценка эффективности инвестиционного портфеля не может ограничиваться лишь суммарной доходностью. Хотя максимизация прибыли является важной целью, всесторонний анализ требует учета сопутствующих рисков. Показатели, такие как коэффициент Шарпа и меры понижающего риска, например, максимальная просадка, позволяют оценить доходность с учетом волатильности и потенциальных потерь. Коэффициент Шарпа, рассчитываемый как $\frac{R_p - R_f}{\sigma_p}$ , где $R_p$ — доходность портфеля, $R_f$ — безрисковая ставка, а $\sigma_p$ — стандартное отклонение доходности портфеля, позволяет сравнить различные инвестиционные стратегии с учетом риска. Максимальная просадка, в свою очередь, показывает наибольшую потерю стоимости портфеля за определенный период, что критически важно для инвесторов, стремящихся к сохранению капитала. Таким образом, использование риск-скорректированных метрик обеспечивает более объективную и полную картину эффективности инвестиций.

Оценка инвестиционных стратегий не должна ограничиваться лишь суммарной прибылью. Более полное представление о результатах достигается при учете показателей, отражающих риски, связанные с потенциальными потерями. Такие метрики, как коэффициент Шарпа и максимальная просадка, позволяют инвесторам оценить, насколько эффективно стратегия компенсирует риски, и сравнить различные подходы с учетом не только потенциального дохода, но и вероятности убытков. Использование этих показателей позволяет сформировать более взвешенное представление о стабильности и надежности инвестиций, что особенно важно в долгосрочной перспективе и при принятии решений в условиях неопределенности рынка.

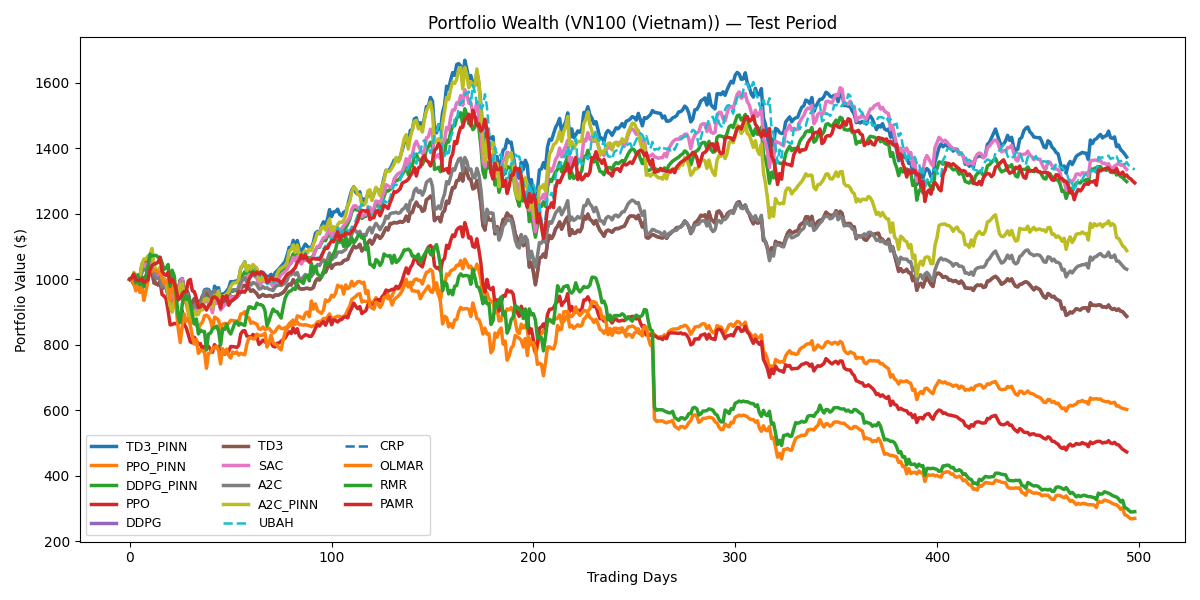
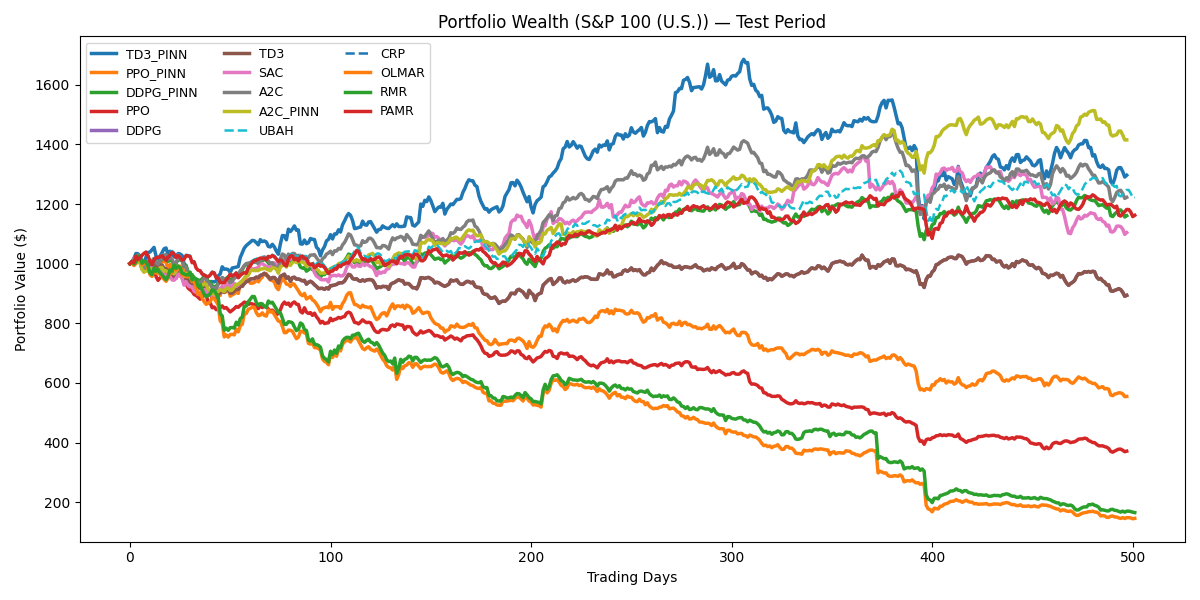
Интеграция обучения с подкреплением, основанного на физических принципах (DRL), в сочетании с тщательной оценкой эффективности, демонстрирует потенциал для создания более стабильных, эффективных и адаптивных стратегий распределения портфеля. Результаты исследований показывают значительное превосходство предложенного подхода: в частности, алгоритм A2C_PINN достиг кумулятивной доходности в 44.66% на американском рынке, что на 10.42% выше, чем у стандартного A2C. Аналогично, вьетнамский рынок показал улучшение коэффициента Шарпа до 0.68 при использовании TD3_PINN, существенно превосходящее показатель стандартного TD3, составивший -0.28. Данные результаты подтверждают, что применение физически обоснованного DRL способствует не только увеличению доходности, но и повышению устойчивости инвестиционных стратегий к неблагоприятным рыночным условиям.

В ходе тестирования на индексе S&P 100 алгоритмы A2C\_PINN и TD3\_PINN продемонстрировали превосходство над другими методами обучения с подкреплением и основанными на правилах, обеспечив более высокую доходность и контроль над рисками.

Представленное исследование демонстрирует элегантную симметрию между принципами физики и оптимизацией финансовых портфелей. Внедрение ньютоновской динамики в алгоритмы глубокого обучения с подкреплением не просто повышает производительность, но и обеспечивает устойчивость и предсказуемость результатов. Как однажды заметил Винтон Серф: «Интернет — это не технология, это способ мышления». Аналогично, данный подход демонстрирует, что фундаментальные законы природы могут быть успешно применены для решения сложных задач в сфере финансов, создавая гармоничное и эффективное решение, где каждая операция имеет чёткий смысл и место в общей системе.

Что Дальше?

Представленная работа, безусловно, демонстрирует потенциал введения физических ограничений, в частности, ньютоновской динамики, в алгоритмы глубокого обучения с подкреплением для финансовых рынков. Однако, следует признать, что корреляция между «физической правдоподобностью» и реальной прибыльностью — не более чем гипотеза, требующая строгой математической формализации. Достаточно ли ньютоновской механики для адекватного моделирования хаотичной природы финансовых процессов? Очевидно, что нет. Необходима разработка более общих принципов инвариантности и сохранения, применимых к сложным системам с нелинейными взаимодействиями.

Ключевым направлением дальнейших исследований представляется расширение класса используемых физических моделей. Вместо упрощенного подхода к ньютоновской динамике, следует исследовать возможности применения принципов термодинамики, статистической механики и даже квантовой теории. Попытки моделирования «рыночного энтропии» или «квантовых флуктуаций» могут оказаться столь же безумными, сколь и плодотворными. Важно помнить, что цель не в том, чтобы «найти правильную физику», а в том, чтобы создать устойчивый и предсказуемый алгоритм.

В конечном итоге, истинный прогресс потребует не просто внедрения физических принципов в существующие алгоритмы, а создания принципиально новых архитектур, основанных на математической строгости и доказательстве корректности. Алгоритм должен быть доказуемо стабильным и эффективным, а не просто «работать на исторических данных». В противном случае, все эти усилия останутся лишь элегантной, но бесполезной математической игрой.

Оригинал статьи: https://arxiv.org/pdf/2602.01388.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-03 15:40