Генеративные модели с контролем рисков: новый подход к оптимизации

Автор: Денис Аветисян

Исследователи предлагают эффективный метод оптимизации, позволяющий учитывать «хвосты» распределений и достигать превосходных результатов в задачах генерации данных.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

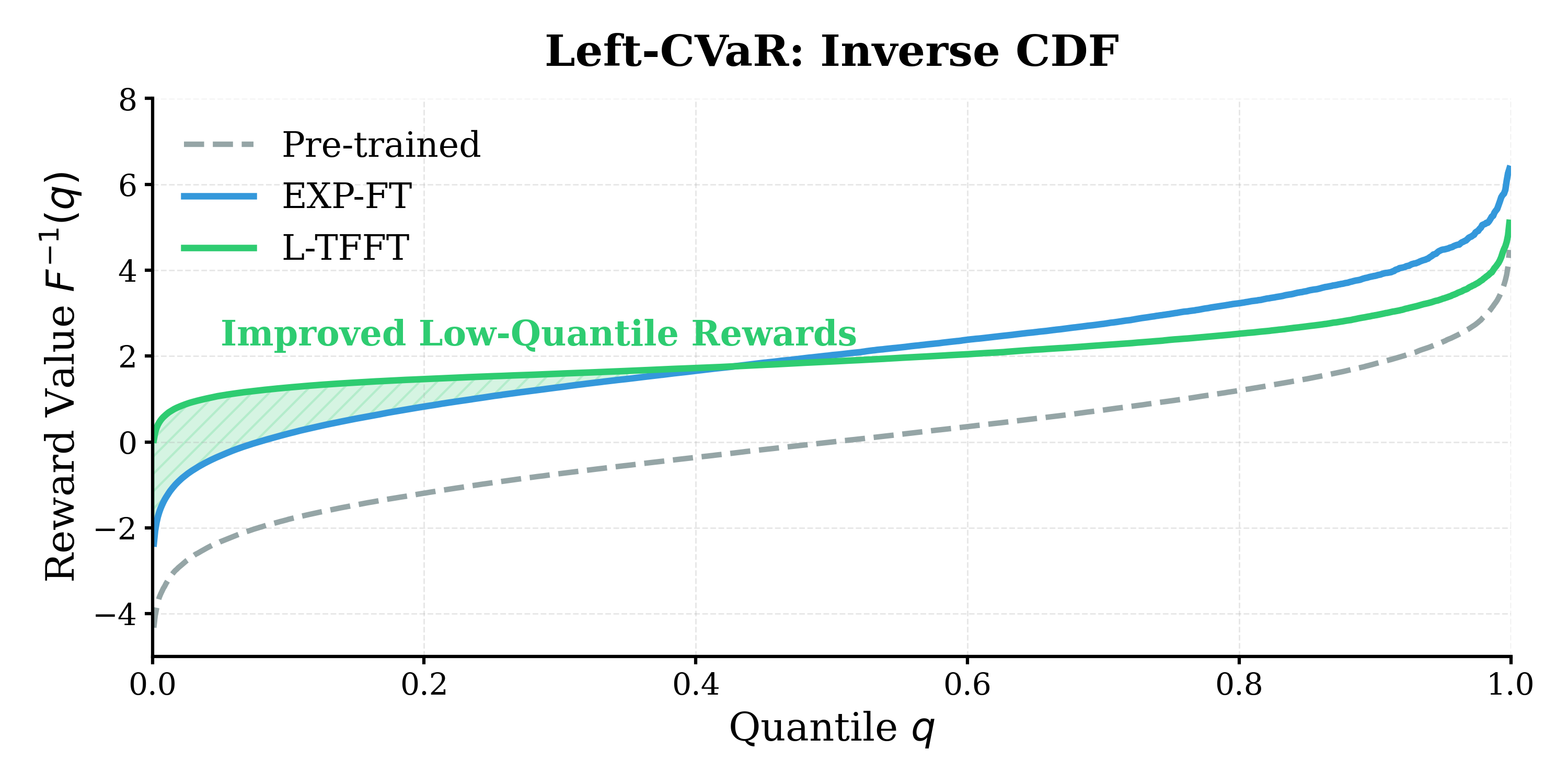
Бесплатный Телеграм канал

Метод L-TFFT демонстрирует превосходство над EXP-FT в области нижнего хвоста распределения вознаграждений [latex]q\in[0,0.2][/latex], что подтверждается анализом обратной кумулятивной функции распределения и указывает на его более эффективное управление рисками в критических сценариях. — Метод L-TFFT демонстрирует превосходство над EXP-FT в области нижнего хвоста распределения вознаграждений $q\in[0,0.2]$ , что подтверждается анализом обратной кумулятивной функции распределения и указывает на его более эффективное управление рисками в критических сценариях.

Предлагаемый фреймворк TFFT разделяет нелинейную задачу оптимизации CVaR на одношаговую процедуру, снижая вычислительные затраты и обеспечивая передовые показатели в дизайне молекул и генерации изображений.

Оптимизация генеративных моделей для конкретных задач часто сводится к максимизации ожидаемой награды, игнорируя критически важные аспекты распределения результатов. В работе ‘Efficient Tail-Aware Generative Optimization via Flow Model Fine-Tuning’ предложен новый алгоритм TFFT, позволяющий эффективно управлять «хвостами» распределения, контролируя как вероятность провалов, так и возможность открытия новых, перспективных решений. Ключевым нововведением является декомпозиция нелинейной задачи оптимизации по условному Value-at-Risk (CVaR) в простой двухэтапный процесс, снижающий вычислительные затраты. Сможет ли TFFT стать стандартом в области генеративного моделирования, открывая новые возможности для задач от молекулярного дизайна до создания изображений?

За пределами средней награды: Ограничения традиционной оптимизации

В генеративном моделировании часто акцент делается на максимизации ожидаемой награды, однако данный подход зачастую игнорирует потенциально катастрофические, хотя и маловероятные, исходы. Такое упрощение может приводить к нестабильной или нежелательной генерации, особенно в областях, где критически важна надежность и безопасность. Вместо комплексного анализа рисков, системы часто оптимизируются под средние значения, не учитывая возможность возникновения редких, но разрушительных событий. В результате, даже незначительная вероятность негативного сценария может оставаться неучтенной, что делает систему уязвимой к неожиданным и неблагоприятным последствиям, несмотря на высокие показатели средней производительности. Игнорирование «хвоста» распределения вероятностей, содержащего эти редкие события, может приводить к серьезным ошибкам и непредсказуемым результатам.

Полагаясь исключительно на максимизацию среднего вознаграждения, генеративные модели часто упускают из виду потенциально разрушительные, хотя и маловероятные, исходы. Эта тенденция особенно критична в областях, где стабильность и надежность имеют первостепенное значение, например, в системах автономного управления или при разработке медицинских препаратов. Использование лишь усредненных значений может привести к генерации нестабильных или нежелательных результатов, поскольку игнорируются “хвосты” распределения вероятностей, где скрываются риски наихудших сценариев. Таким образом, оптимизация, основанная только на средних показателях, может оказаться недостаточной для обеспечения безопасности и предсказуемости в критически важных приложениях, подчеркивая необходимость учета не только ожидаемого вознаграждения, но и вероятности экстремальных событий.

Традиционные методы генеративного моделирования часто упускают из виду критически важный аспект — управление “хвостовым риском”, то есть вероятностью наступления крайне неблагоприятных событий. В то время как оптимизация фокусируется на максимизации ожидаемой награды, существует опасность игнорирования редких, но потенциально катастрофических исходов. Предложенный подход позволяет установить чувствительность между истинным и аппроксимированным распределениями, гарантируя, что расхождение между ними, измеряемое с помощью $KL$ -дивергенции, не превышает $< 2δ/α(1-β)$ . Это означает, что вероятность наступления экстремальных событий эффективно контролируется, обеспечивая более стабильные и предсказуемые результаты генерации, особенно в приложениях, где крайне важна надежность и безопасность.

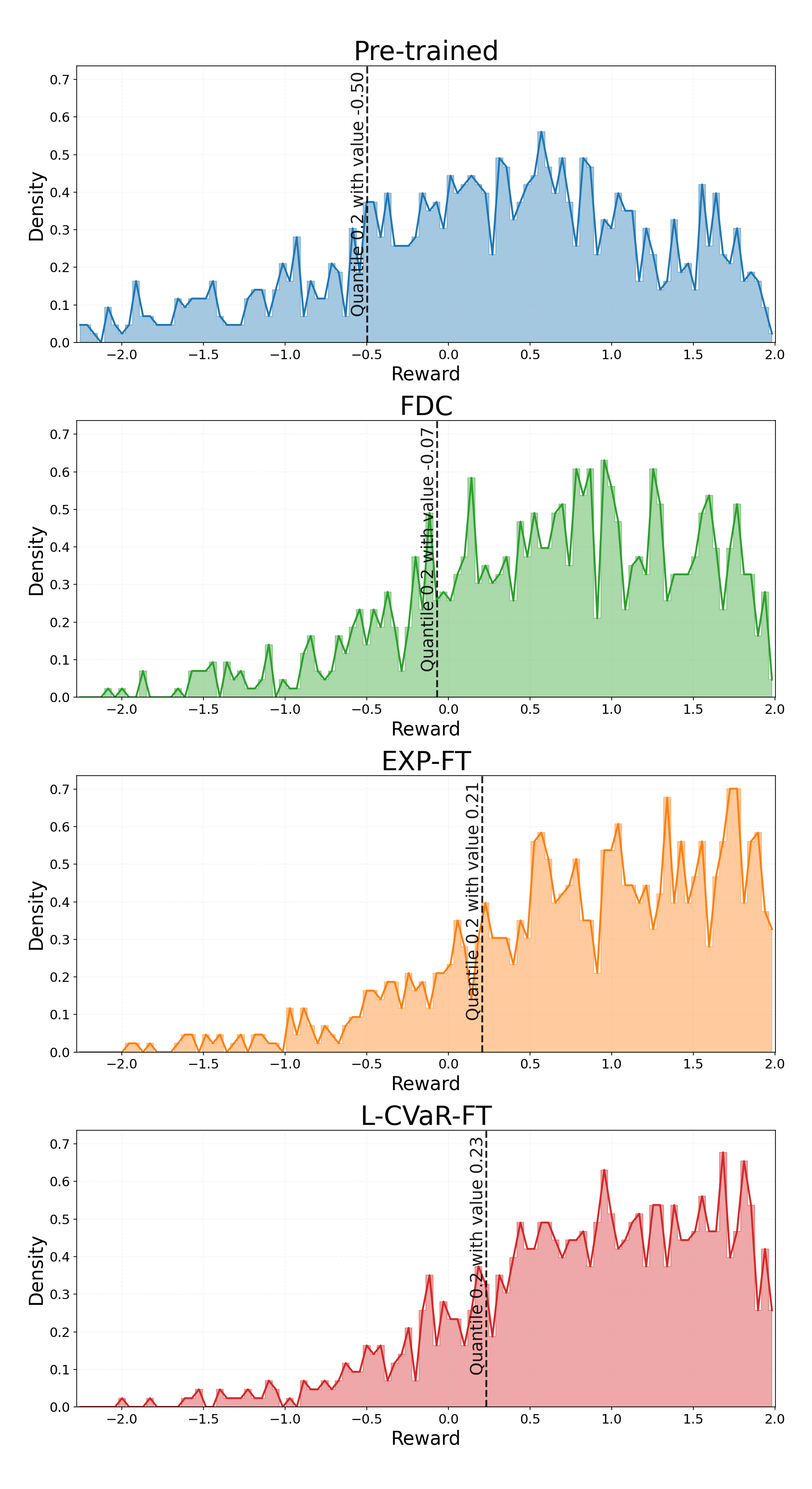
Анализ данных, представленных на рисунке 11, демонстрирует эффективность метода L-TFFT в подавлении вероятности наступления неблагоприятных сценариев, относящихся к “хвосту” распределения. В частности, наблюдается повышение значения 20-го квантиля, что свидетельствует о смещении вероятностной массы от наихудших исходов к более благоприятным. Это означает, что L-TFFT позволяет значительно снизить риск возникновения экстремальных событий, улучшая стабильность и надежность генерируемых результатов, особенно в областях, где даже небольшая вероятность катастрофических последствий является неприемлемой. По сути, метод эффективно ограничивает вероятность наступления нежелательных сценариев, обеспечивая более управляемое и предсказуемое поведение системы.

Модель L-TFFT демонстрирует подавление вероятности неблагоприятных сценариев (нижнего хвоста распределения наград) по сравнению с базовыми моделями, что подтверждается более высоким значением 20-го квантиля.

Управление хвостами: Новая парадигма оптимизации

Традиционная оптимизация генеративных моделей часто фокусируется на максимизации средней награды, игнорируя риски, связанные с редкими, но значимыми событиями. Оптимизация, учитывающая хвосты распределения (tail-aware generative optimization), переходит к прямому анализу и управлению этими рисками. Такой подход позволяет учитывать вероятность наступления событий с высокой негативной или позитивной отдачей, даже если их вероятность мала. Вместо простого увеличения среднего значения, оптимизация направлена на формирование распределения, которое минимизирует потенциальные убытки и максимизирует возможности в области экстремальных значений, обеспечивая более надежные и стабильные результаты, особенно в критически важных приложениях.

Условная ценность под риском (Conditional Value-at-Risk, CVaR) представляет собой связную меру риска, позволяющую точно контролировать хвосты распределения вероятностей. В отличие от стандартного Value-at-Risk (VaR), который лишь указывает на порог потерь, CVaR вычисляет среднее значение потерь, превышающих этот порог. Это делает CVaR более чувствительным к экстремальным событиям и обеспечивает более полное представление о риске, особенно в сценариях, где важна минимизация потенциальных убытков в «худших» случаях. Математически, $CVaR_{\alpha}(X) = E[X | X \le VaR_{\alpha}(X)]$ , где α — уровень доверия, а $VaR_{\alpha}(X)$ — значение Value-at-Risk на уровне α. Использование CVaR в оптимизационных задачах позволяет напрямую управлять вероятностью неблагоприятных событий и повышать устойчивость моделей.

Внедрение принципов неприятия риска в процесс оптимизации генеративных моделей позволяет повысить их устойчивость и стабильность. В отличие от традиционных методов, фокусирующихся на максимизации среднего значения вознаграждения, оптимизация с учетом неприятия риска явно учитывает вероятность наступления неблагоприятных событий с высокой стоимостью. Это достигается путем введения параметров, определяющих степень неприятия риска, что позволяет контролировать распределение вероятностей и минимизировать потери в «хвостах» распределения. Например, использование таких метрик, как Conditional Value-at-Risk (CVaR), позволяет точно управлять уровнем риска и гарантировать, что модель будет менее подвержена значительным отклонениям от ожидаемых результатов, обеспечивая более предсказуемое и надежное поведение в различных сценариях.

Применение подхода, ориентированного на контроль “хвостов” распределений, особенно эффективно в областях, связанных с высокими рисками, таких как молекулярный дизайн и финансовое моделирование. Экспериментальные данные показывают, что оптимальные результаты достигаются при умеренном уровне риска; в частности, максимальная достоверность (Validity Rate) наблюдается при значении параметра $β = 0.9$ . Это свидетельствует о том, что предложенный метод позволяет находить баланс между достижением высоких наград и минимизацией вероятности нежелательных событий, критичных для данных областей применения.

Результаты, представленные на Рисунке 9, демонстрируют различную производительность алгоритмов R-TFFT и L-TFFT в зависимости от квантиля распределения наград. R-TFFT (Right-TFFT) показывает более высокие значения наград в области высоких квантилей, что свидетельствует о его эффективности в достижении оптимальных результатов при благоприятных сценариях. В то же время, L-TFFT (Left-TFFT) превосходит R-TFFT в области низких квантилей, указывая на его повышенную устойчивость к неблагоприятным событиям и способность минимизировать риски в критических ситуациях. Данное различие в производительности подчеркивает важность выбора алгоритма оптимизации в зависимости от специфических требований задачи и допустимого уровня риска.

В двумерном примере, метод R-TFFT обеспечивает более высокие награды в области высоких квантилей, а L-TFFT - в области низких квантилей, что отражено в обратных кумулятивных функциях распределения (CDF) предобученной и дообученных моделей. — В двумерном примере, метод R-TFFT обеспечивает более высокие награды в области высоких квантилей, а L-TFFT — в области низких квантилей, что отражено в обратных кумулятивных функциях распределения (CDF) предобученной и дообученных моделей.

Тонкая настройка для контроля хвостов: Практический подход

Метод тонкой настройки с учетом хвостов распределения (Tail-Aware Flow Fine-Tuning, TFFT) представляет собой подход к непосредственной оптимизации генеративных моделей для контроля поведения в области хвостов выходного распределения. В отличие от традиционных методов, которые неявно влияют на хвосты через оптимизацию всей модели, TFFT позволяет напрямую задавать и минимизировать риск в этих областях. Это достигается путем включения в процесс обучения целевой функции, явно учитывающей характеристики хвостов распределения, что позволяет более эффективно контролировать вероятность генерации редких, но потенциально важных событий или аномалий. TFFT обеспечивает возможность точного управления формой хвостов, повышая устойчивость и производительность модели в различных сценариях.

Метод Tail-Aware Flow Fine-Tuning (TFFT) использует вариационную двойственную формулировку для эффективного вычисления и минимизации риска в хвостах распределения. Вместо прямого вычисления рисковых метрик, требующего больших вычислительных затрат, TFFT переформулирует задачу минимизации риска как задачу максимизации нижней границы, используя двойственную теорию. Это позволяет заменить сложную оптимизацию по исходному распределению оптимизацией по вспомогательному распределению, что значительно снижает вычислительную сложность. Такой подход обеспечивает эффективную оценку и контроль над вероятностью редких, но значимых событий в хвостах генерируемого распределения, что критически важно для повышения надежности и производительности модели.

В процессе тонкой настройки модели, для предотвращения переобучения и стимулирования исследования пространства решений, используется регуляризация энтропии. Этот метод добавляет к целевой функции штраф, пропорциональный энтропии выходного распределения. $H(p) = - \sum_{i} p(i) \log p(i)$ . Увеличение энтропии способствует более равномерному распределению вероятностей, что позволяет модели избегать чрезмерной уверенности в отдельных решениях и лучше обобщать данные. Регуляризация энтропии эффективно предотвращает застревание в локальных минимумах и способствует нахождению более робастных и устойчивых решений, особенно в задачах генерации, где необходимо разнообразие выходных данных.

Метод Tail-Aware Flow Fine-Tuning (TFFT) обеспечивает точный контроль над «хвостами» генерируемого распределения, повышая устойчивость и производительность модели. Достигается это за счет комбинирования вариационного двойственного подхода и регуляризации энтропией. В ходе исследований была продемонстрирована сходимость метода в зависимости от числа выборок M и числа итераций N, которая количественно оценивается как $O(1/\sqrt{M}) + O(1/N)$ . Данный показатель сходимости подтверждает эффективность TFFT в достижении целевого распределения при увеличении числа выборок и итераций.

На рисунке 2 продемонстрировано, как Tail-Aware Flow Fine-Tuning (TFFT) позволяет избежать дорогостоящего итеративного цикла, характерного для традиционных методов оптимизации. В отличие от подходов, требующих многократных прогонов генеративной модели для достижения желаемого распределения, TFFT обеспечивает сходимость к целевому распределению за один проход. Это достигается за счет использования вариационной двойной формулировки и оптимизации непосредственно риска в хвостах распределения, что значительно сокращает вычислительные затраты и время обучения. Визуализация на рисунке 2 иллюстрирует, что TFFT быстро приближается к целевой функции, минуя необходимость в многочисленных итерациях, что подтверждает эффективность предложенного подхода.

В ходе применения правила обновления FDC ([latex]13[/latex]), распределения [latex]p_k^k[/latex] сходятся к целевому распределению [latex]p_R^*[/latex] ([latex]6[/latex]), что эмпирически подтверждает теоретические выводы и демонстрирует, что TFFT позволяет избежать дорогостоящего итеративного цикла. — В ходе применения правила обновления FDC ( $13$ ), распределения $p_k^k$ сходятся к целевому распределению $p_R^*$ ( $6$ ), что эмпирически подтверждает теоретические выводы и демонстрирует, что TFFT позволяет избежать дорогостоящего итеративного цикла.

Применение и будущие направления: За пределами смягчения рисков

Оптимизация с учетом «хвоста» распределения вероятностей открывает новые горизонты в таких областях, как молекулярный дизайн. Этот подход позволяет создавать соединения с заданными, оптимизированными свойствами и, что критически важно, минимизированными рисками, связанными с их потенциальной токсичностью или нестабильностью. Вместо слепого поиска наиболее вероятных кандидатов, оптимизация с учетом «хвоста» исследует менее вероятные, но потенциально более выгодные молекулярные структуры, расширяя пространство поиска и повышая шансы на обнаружение соединений с уникальными и желаемыми характеристиками. Подобная стратегия особенно важна при разработке новых лекарственных препаратов и материалов, где даже небольшие улучшения в свойствах могут привести к значительным прорывам.

Повышение надежности генеративных моделей имеет критическое значение для применений в чувствительных областях, таких как финансовый прогнозирование. Подход, учитывающий «хвосты» распределений вероятностей, позволяет создавать модели, менее подверженные генерации экстремальных или нереалистичных сценариев, что особенно важно при прогнозировании финансовых рынков. Традиционные модели часто испытывают трудности с оценкой рисков, связанных с маловероятными, но потенциально катастрофическими событиями. Учет «хвостов» позволяет более точно моделировать эти риски, улучшая стабильность и достоверность прогнозов, а также снижая вероятность принятия ошибочных финансовых решений. Это достигается за счет более тщательного анализа и учета данных, находящихся в «хвостах» распределений, что позволяет выявлять и учитывать ранее незамеченные закономерности и факторы, влияющие на финансовые рынки.

В рамках адаптации алгоритмов оптимизации с учетом “хвостов” распределений, концепция поиска новизны играет ключевую роль в достижении баланса между исследованием новых возможностей и использованием уже известных, эффективных решений. Внедрение механизмов, стимулирующих генерацию и оценку нестандартных кандидатов, позволяет избежать застревания в локальных оптимумах и расширяет пространство поиска, особенно в задачах, где желаемые свойства находятся в редкой области параметров. Такой подход позволяет не только повысить качество генерируемых решений, но и обеспечить их разнообразие, что критически важно для приложений, требующих устойчивости к изменениям и адаптации к новым условиям. Использование стратегий, поощряющих “исследование” новых областей пространства решений, в сочетании с оценкой их потенциала, обеспечивает более эффективный поиск оптимальных решений в сложных задачах оптимизации.

Перспективные исследования направлены на адаптацию методов, учитывающих «хвосты» распределений, к более сложным генеративным архитектурам, таким как диффузионные и потоковые генеративные модели. Ожидается, что интеграция этих подходов позволит значительно повысить надежность и возможности указанных моделей, особенно в задачах, требующих генерации стабильных и качественных образцов. Успешное расширение области применения на более сложные архитектуры откроет новые горизонты в разработке генеративных моделей, обеспечивая повышенную устойчивость к нежелательным результатам и позволяя создавать более реалистичные и полезные данные. Такая адаптация позволит преодолеть ограничения существующих методов и расширить спектр решаемых задач, в особенности в областях, где критически важна предсказуемость и безопасность генерируемых данных.

Результаты, представленные на рисунке 5, наглядно демонстрируют превосходство разработанного метода R-TFFT в обнаружении стабильных кандидатов. В ходе сравнительного анализа было установлено, что R-TFFT способен генерировать соединения с показателями стабильности, достигающими 5059 единиц, что значительно превышает лучшие результаты, полученные с использованием методов EXP-FT (1069 единиц) и FDC (2012 единиц). Такое существенное улучшение указывает на эффективность предложенного подхода в оптимизации свойств молекул и открывает новые возможности для разработки соединений с заданными характеристиками, превосходящих существующие аналоги по стабильности и, следовательно, по потенциальной применимости.

Метод R-TFFT позволяет обнаруживать молекулы с существенно большей стабильностью (до оценки 5059), чем EXP-FT (1069) и FDC (2012), что подтверждает его способность исследовать область молекул с экстремально высокой наградой.

Исследование представляет собой элегантное решение проблемы оптимизации генеративных моделей с учётом рисков в «хвосте» распределения. Авторы предлагают метод TFFT, который, подобно тщательно выстроенному математическому доказательству, отделяет нелинейную функцию CVaR от основного процесса оптимизации. Это позволяет значительно снизить вычислительные затраты, сохраняя при этом высокую эффективность в задачах, требующих точного контроля над генерацией, таких как дизайн молекул и создание изображений. Как однажды заметила Барбара Лисков: «Программы должны быть разработаны так, чтобы их можно было понять, а не просто чтобы они работали». Именно эта ясность и математическая чистота прослеживается в предложенном подходе к оптимизации генеративных моделей.

Что дальше?

Представленная работа, несомненно, представляет шаг вперед в области генеративной оптимизации, особенно в контексте управления рисками в «хвосте» распределения. Однако, стоит признать, что элегантность упрощения нелинейной задачи CVaR посредством одношаговой процедуры не решает фундаментальную проблему: адекватности самой модели потока для репрезентации сложных, многомерных целевых функций. По сути, перенос вычислительной нагрузки с оптимизации на этап обучения модели потока лишь отодвигает проблему, а не устраняет её.

Будущие исследования, вероятно, сосредоточатся на разработке более гибких и выразительных моделей потоков, способных улавливать тонкие нюансы целевых функций, особенно в задачах, где данные ограничены или зашумлены. Ключевым направлением представляется исследование гибридных подходов, сочетающих преимущества моделей потоков с возможностями других генеративных моделей, таких как вариационные автоэнкодеры или генеративно-состязательные сети. В конечном счете, истинная эффективность будет заключаться не в скорости вычислений, а в математической точности представления реальности.

В хаосе данных спасает только математическая дисциплина. Дальнейшее развитие этого направления требует не просто улучшения алгоритмов, но и углубленного понимания теоретических основ генеративного моделирования и оптимизации. В противном случае, мы рискуем создать лишь иллюзию прогресса, основанную на эмпирических наблюдениях, а не на строгих доказательствах.

Оригинал статьи: https://arxiv.org/pdf/2602.16796.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-20 10:08