Геометрия Ликвидности: Новый Взгляд на Порядок Книги

Автор: Денис Аветисян

Исследование предлагает оригинальную модель, в которой асимметрия ликвидности в биржевых стаканах возникает не из поведения трейдеров, а как следствие геометрических деформаций.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал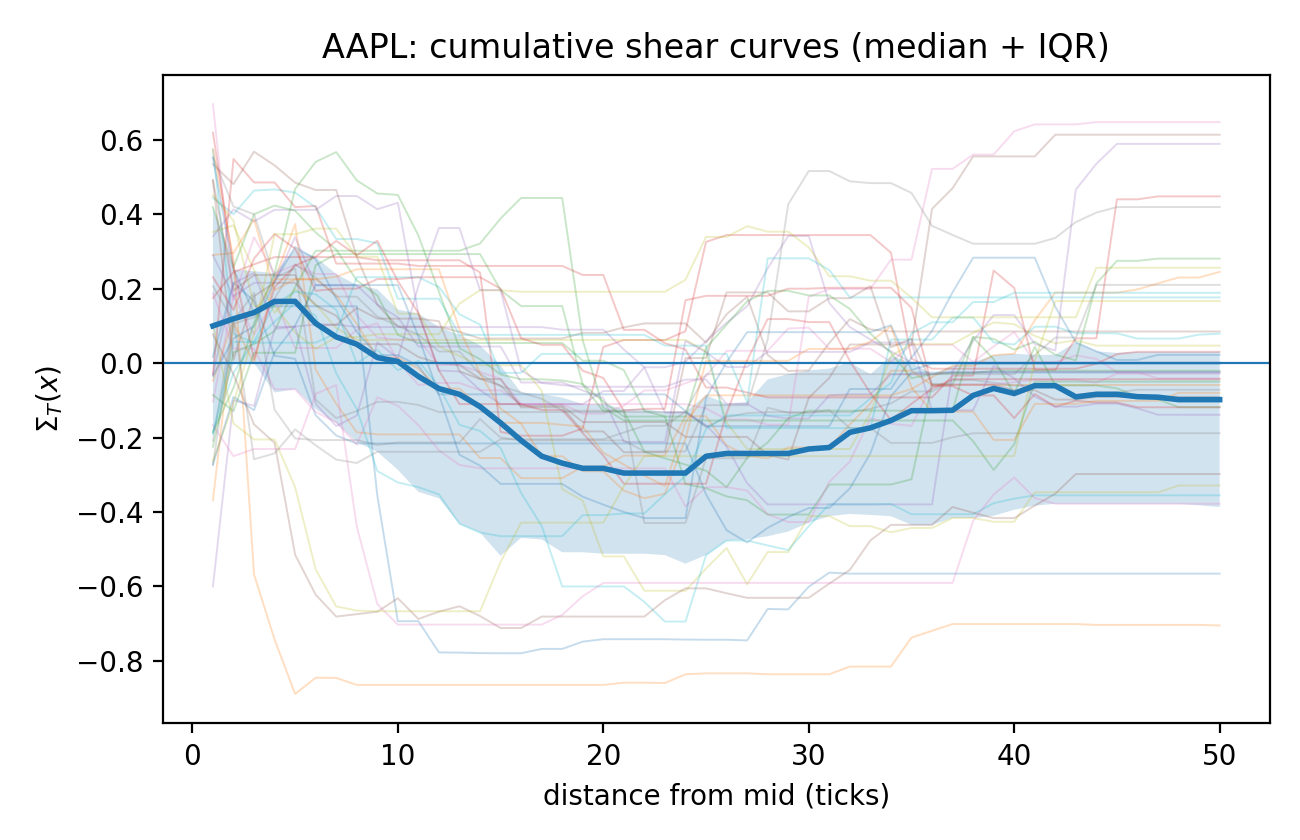

Наблюдаемый кумулятивный сдвиг для AAPL указывает на макроскопическую деформацию спроецированной геометрии ликвидности, исключая локализованные микроструктурные эффекты как причину наблюдаемого явления.

В данной работе предложена прегеометрическая модель, рассматривающая ликвидность и асимметрию биржевого стакана как эмерджентные геометрические сдвиги, возникающие в спроецированной реляционной системе, независимые от ценовой динамики.

Традиционные модели анализа биржевых стаканов часто рассматривают ликвидность как результат поведения агентов, упуская возможность рассмотрения ее как фундаментальное геометрическое свойство. В работе «Directional Liquidity and Geometric Shear in Pregeometric Order Books» предложена прегеометрическая модель, в которой асимметрия ликвидности возникает не из действий участников рынка, а как результат геометрических деформаций — сдвигов — спроецированной реляционной системы, независимых от ценовой динамики. Показано, что эти сдвиги ограничивают распределение ликвидности гамма-подобной функцией, обнаруживаемой в данных высокочастотной торговли. Способна ли эта геометрия стать основой для более точного прогнозирования движения цен и разработки новых торговых стратегий?

По ту сторону традиций: Реляционная основа рыночной динамики

Традиционные финансовые модели зачастую рассматривают формирование цен как процесс, обусловленный действиями независимых участников рынка, упуская из виду фундаментальную роль взаимосвязанности. Такой подход предполагает, что каждый трейдер принимает решения, исходя исключительно из собственной информации и анализа, игнорируя влияние, которое оказывают на него другие участники и их поведение. Однако, реальные финансовые рынки представляют собой сложные системы, где решения одного участника неизбежно влияют на решения других, создавая каскадные эффекты и формируя коллективное поведение. Пренебрежение этими взаимосвязями приводит к упрощенным моделям, которые не способны адекватно отразить динамику рынка и предсказать его реакцию на различные события. Недооценка сетевой структуры финансовых рынков, где информация и влияние распространяются через сложные связи между участниками, является серьезным ограничением для создания точных и надежных прогнозов.

Предлагается принципиально новый взгляд на финансовые рынки, рассматривающий их не как совокупность независимых действий, а как сложные системы, в которых коллективное поведение возникает из глубинной «Реляционной Подложки» взаимодействий. Данный подход подчеркивает, что наблюдаемые рыночные паттерны являются эмерджентными свойствами не отдельных сделок, а сети взаимосвязей между участниками. Вместо анализа изолированных транзакций, внимание фокусируется на структуре и динамике этих связей, которые формируют основу для возникновения трендов и колебаний. Понимание этой реляционной основы позволяет рассматривать рынок как самоорганизующуюся систему, где поведение каждого участника опосредуется влиянием других, что открывает новые возможности для моделирования и прогнозирования рыночной динамики.

Вместо фокусировки на отдельных сделках, современный анализ финансовых рынков всё больше внимания уделяет изучению взаимосвязей между участниками. Наблюдаемые рыночные паттерны формируются не случайно, а являются результатом коллективного поведения, обусловленного сложной сетью отношений между трейдерами, институциональными инвесторами и другими игроками. Исследования показывают, что структура этих взаимосвязей — кто с кем взаимодействует, как часто и с какими целями — оказывает существенное влияние на динамику цен и объемов торгов. Понимание этих отношений позволяет перейти от анализа отдельных событий к прогнозированию общих тенденций и повышению точности финансовых моделей, раскрывая скрытые механизмы формирования рыночной конъюнктуры.

Признание взаимосвязей между участниками рынка основополагающим фактором является ключевым для создания более устойчивых и прогностических моделей динамики рынка. Традиционные подходы, фокусирующиеся на индивидуальных сделках и независимых агентах, зачастую упускают из виду, что именно сеть взаимодействий — «реляционная подложка», как ее можно назвать — формирует наблюдаемые паттерны. Исследования показывают, что коллективное поведение возникает не случайно, а является результатом сложной системы влияний и зависимостей между трейдерами, инвесторами и другими участниками. Понимание структуры этих взаимосвязей, их силы и характера позволяет не просто описывать рыночные явления, но и предсказывать их развитие с большей точностью, учитывая, что изменения в одной части сети могут быстро распространяться и приводить к каскадным эффектам.

Геометрия книги ордеров: Картография ликвидности

Геометрия книги ордеров представляет собой новый подход к пониманию распределения ликвидности, рассматривающий уровни цен не как отдельные точки, а как координаты в геометрическом пространстве. В отличие от традиционных методов анализа, которые оперируют дискретными ценами, данный подход позволяет рассматривать книгу ордеров как многомерную структуру, где каждая цена и объем заявок определяют положение в этом пространстве. Это позволяет анализировать взаимосвязи между различными уровнями цен и объемами, выявляя закономерности, скрытые при использовании стандартных инструментов. Формально, каждый уровень цены может быть представлен как координата в $n$ -мерном пространстве, где $n$ — количество уровней цен, рассматриваемых в анализе. Такое представление позволяет применять методы геометрического анализа, такие как вычисление расстояний, углов и объемов, для количественной оценки структуры ликвидности.

Метод “Наблюдательной проекции” позволяет сопоставить внутреннюю, реляционную структуру книги ордеров с наблюдаемыми уровнями цен, выявляя закономерности, скрытые при использовании традиционных методов анализа. В основе метода лежит сопоставление взаимосвязей между ордерами (реляционный субстрат) с конкретными ценами, по которым эти ордера размещены. Эта проекция позволяет представить книгу ордеров не как набор изолированных цен, а как многомерное пространство, где близость ордеров в этом пространстве отражает их взаимосвязь и влияние на формирование ликвидности. В результате анализа спроецированной структуры можно идентифицировать кластеры ордеров, зоны поддержки и сопротивления, а также предсказывать поведение цены на основе изменений в реляционном субстрате.

Структура бид-аск (Bid-Ask), средняя цена (Mid Price) и дрейф средней цены (Mid-Price Drift) являются ключевыми компонентами геометрического представления книги ордеров. Бид-аск определяет минимальную цену продажи и максимальную цену покупки, формируя базовые координаты в данном пространстве. Средняя цена, рассчитываемая как $(Bid + Ask) / 2$ , служит центральной точкой отсчета и позволяет оценить текущий уровень равновесия. Дрейф средней цены, отражающий изменение средней цены во времени, предоставляет информацию о динамике ликвидности и потенциальных направлениях движения цены. В совокупности эти элементы позволяют построить многомерную карту ликвидности, описывающую не только статические уровни цены, но и их взаимосвязь и эволюцию во времени.

Геометрический подход к анализу стакана заявок позволяет выявлять и количественно оценивать присущие ему структурные особенности. В частности, анализ распределения ликвидности на различных ценовых уровнях, рассматриваемый как координаты в многомерном пространстве, дает возможность точно определить концентрацию заявок, глубину рынка и асимметрию спроса и предложения. Количественная оценка таких параметров, как объем заявок на каждом уровне, расстояние между крупными кластерами заявок и скорость изменения этих параметров во времени ( $\Delta V(p, t)$ , где $V$ — объем, $p$ — цена, $t$ — время), позволяет выявить закономерности в формировании и динамике ликвидности, которые остаются незамеченными при традиционном анализе стакана заявок. Это, в свою очередь, способствует более точному прогнозированию рыночных движений и разработке эффективных торговых стратегий.

Зависимость амплитуды сдвига от изменения средней цены акции Apple (AAPL) демонстрирует корреляцию между этими параметрами.

Гамма-геометрия: Функциональное описание кумулятивной ликвидности

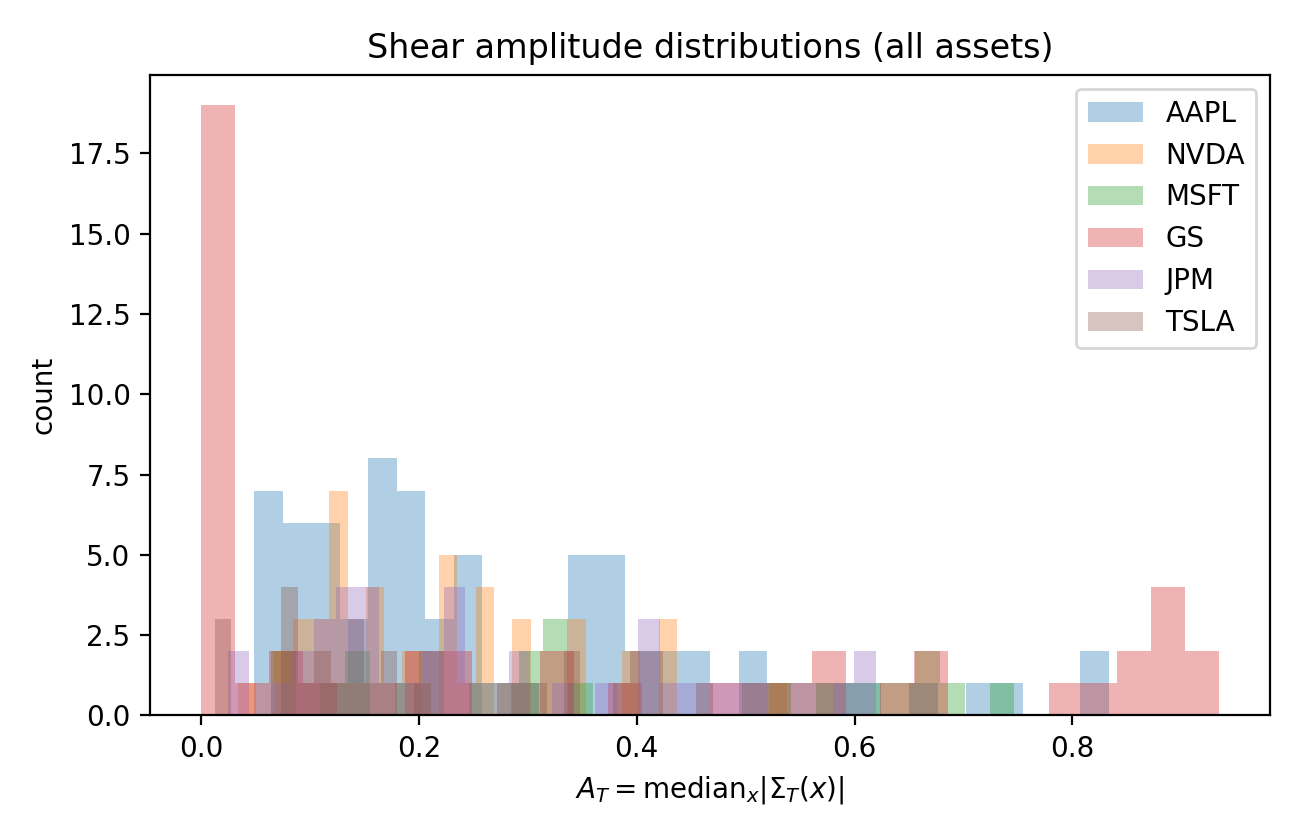
Исследование показывает, что профиль кумулятивной ликвидности в книге ордеров точно описывается гамма-распределением. Гамма-геометрия, основанная на анализе данных, позволяет моделировать распределение ликвидности, учитывая концентрацию ордеров на различных ценовых уровнях. Кумулятивная ликвидность, определяемая как суммарный объем ордеров на всех уровнях цены ниже текущей, демонстрирует характерную форму, соответствующую гамма-функции $\Gamma(x)$ . Это позволяет использовать гамма-распределение для количественной оценки и прогнозирования доступности ликвидности на различных глубинах книги ордеров.

В основе моделирования кумулятивной ликвидности лежит гипотеза единого масштаба (Single-Scale Hypothesis), утверждающая, что распределение ликвидности в книге ордеров в конкретный момент времени определяется доминирующей характеристической длиной. Данная гипотеза предполагает, что вариации в ликвидности подчиняются экспоненциальному убыванию, определяемому этим масштабом, что позволяет эффективно описывать кумулятивное распределение ликвидности с использованием гамма-распределения. Фактически, гипотеза предполагает, что несмотря на сложность динамики книги ордеров, ее статистические свойства могут быть сведены к одному параметру, характеризующему типичное расстояние между ордерами.

Для валидации применимости гамма-распределения к моделированию наблюдаемых паттернов ликвидности был использован критерий Акаике (Akaike Information Criterion, AIC). Результаты анализа показали, что интегрированная гамма-модель демонстрирует стабильно более высокую предсказательную способность по сравнению с альтернативными моделями, такими как степенное распределение (power-law), экспоненциальное распределение и логнормальное распределение. Превосходство интегрированной гамма-модели было подтверждено на различных активах и для обеих сторон книги ордеров (bid и ask), что указывает на ее универсальность и надежность в описании кумулятивной ликвидности.

Интегрированная гамма-функция обеспечивает полное описание кумулятивной ликвидности, устанавливая связь между геометрической структурой и количественными показателями. Данная модель позволяет представить кумулятивное распределение ликвидности как интеграл от гамма-распределения $\Gamma(k, \theta)$ , где $k$ — параметр формы, а θ — параметр масштаба. Этот подход позволяет связать параметры гамма-распределения с наблюдаемыми характеристиками ликвидности, такими как глубина рынка и объем торгов, что позволяет количественно оценивать и прогнозировать поведение ликвидности на различных уровнях цен. В частности, параметр масштаба θ определяет характерную длину масштаба ликвидности, а параметр формы $k$ описывает ее концентрацию или разброс.

Амплитуды сдвига распределены по активам, демонстрируя вариативность их подверженности деформациям.

Раскрывая асимметрию: Дисбаланс ликвидности и геометрический сдвиг

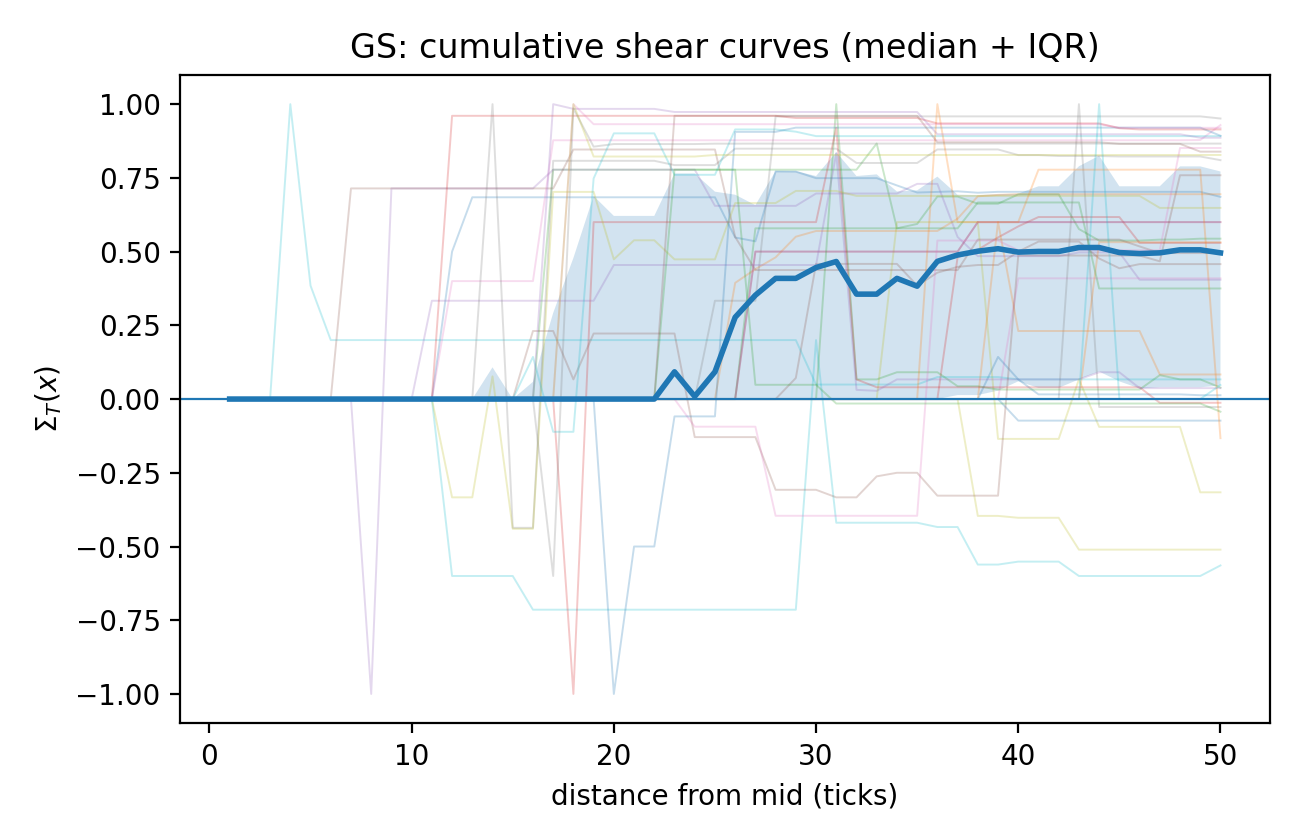
Предлагаемый подход позволяет количественно оценить асимметрию ликвидности, выявляя дисбаланс между сторонами заявок на покупку и продажу в стакане ордеров. Традиционно, анализ ликвидности ограничивается общими показателями объема, однако данная методика фокусируется на распределении ликвидности, оценивая, насколько сильно одна сторона стакана ордеров превосходит другую. Это позволяет не только зафиксировать сам факт дисбаланса, но и измерить его величину, что критически важно для понимания потенциального влияния на ценообразование и стабильность рынка. Использование количественной оценки асимметрии ликвидности открывает новые возможности для разработки более точных моделей прогнозирования и управления рисками, а также для выявления потенциальных манипуляций на рынке.

В рамках исследования предложена концепция “Геометрического Сдвига” как количественной меры асимметрии ликвидности на финансовых рынках. Данный показатель напрямую связывает наблюдаемые изменения цен с базовой деформацией распределения ликвидности, представляя собой не просто статистическое отклонение, но и визуально интерпретируемую метрику. Геометрический Сдвиг позволяет оценить степень искажения формы книги ордеров, отражая дисбаланс между количеством заявок на покупку и продажу по различным ценам. $Ш = \in t_{\mathbb{R}} |L(p + \delta) - L(p - \delta)| dp$ , где $L(p)$ — функция плотности ликвидности по цене $p$ , а интеграл вычисляется по диапазону цен. Такой подход позволяет не только выявлять моменты асимметрии, но и количественно оценивать ее интенсивность, открывая возможности для более глубокого анализа динамики рынка и разработки более точных моделей ценообразования.

Статистический анализ, основанный на применении непараметрической бутстрап-перевыборки с 95% доверительными интервалами, подтвердил устойчивость выявленных закономерностей смещения ликвидности. Данный метод позволил оценить надёжность обнаруженных паттернов, исключая вероятность случайных флуктуаций. Полученные доверительные интервалы не пересекают нулевую отметку, что свидетельствует о статистической значимости наблюдаемого смещения и его устойчивости к изменениям в данных. Такой подход к анализу гарантирует, что выявленные закономерности не являются артефактами конкретного набора данных, а отражают фундаментальные характеристики динамики ликвидности, что повышает доверие к результатам исследования и открывает возможности для их практического применения.

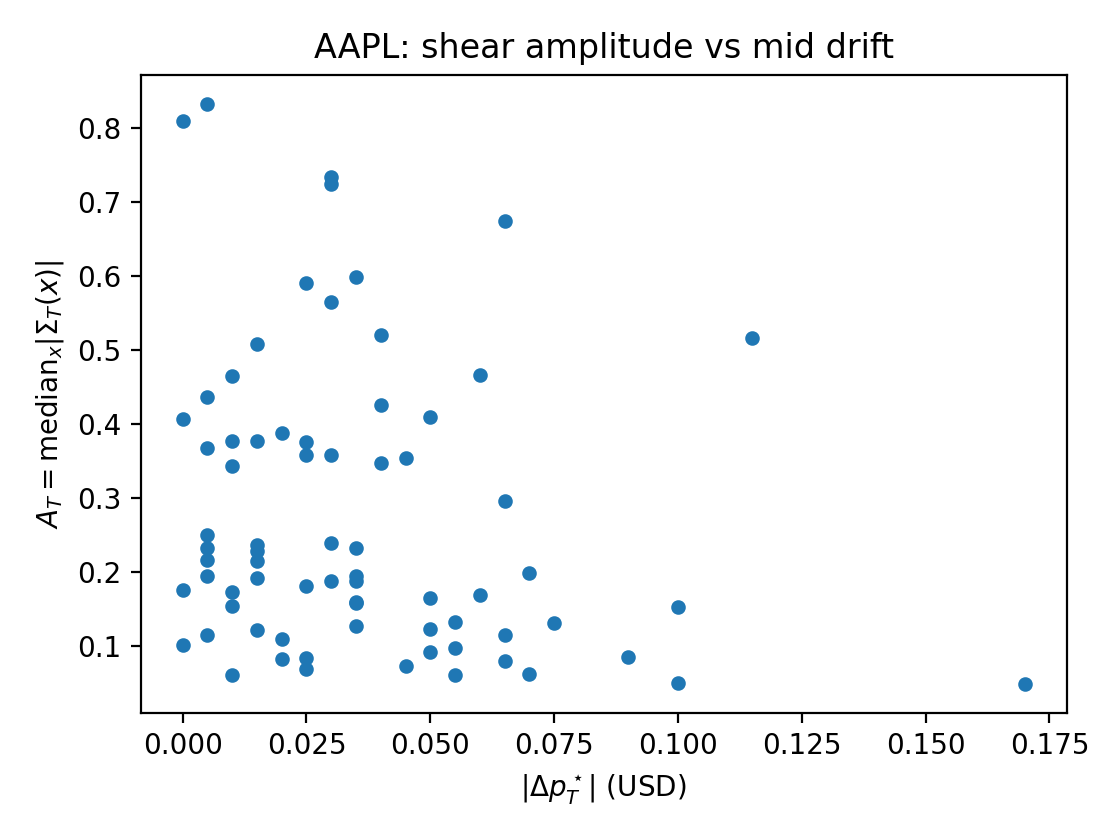
Анализ корреляции между амплитудой сдвига (Shear Amplitude) и абсолютным смещением средней цены (Absolute Mid-Price Displacement) демонстрирует, что данный показатель в большинстве случаев не имеет статистически значимой связи с направлением и величиной ценовых движений (p > 0.05 после коррекции на множественные сравнения). Это указывает на то, что геометрический сдвиг, как мера асимметрии ликвидности, является самостоятельным феноменом, не являющимся простым следствием колебаний цены. Полученные результаты позволяют предположить, что наблюдаемая деформация ликвидности может являться предшествующим фактором, влияющим на дальнейшую динамику рынка, или же отражать скрытые процессы, не зависящие от непосредственного ценообразования.

Накопленное сдвиговое поле для GS демонстрирует распределение деформаций сдвига.

Данные о стакане ордеров — лишь проекция более глубокой, скрытой структуры. Статья предлагает рассматривать ликвидность и асимметрию не как результат действий участников, а как проявление геометрических деформаций, возникающих в некоем ‘прегеометрическом’ порядке. Это напоминает о том, как шум может маскировать истинную форму, а кажущаяся упорядоченность — быть лишь иллюзией, созданной нашим восприятием. Карл Саган однажды сказал: «Мы сделаны из звёздной пыли». Подобно этому, стакан ордеров — это не просто цифры, а отголосок фундаментальной, геометрической реальности, проявляющийся в искажениях и деформациях, как сдвиг (shear deformation) в многомерном пространстве. Истинный порядок лежит за пределами видимого, в геометрии отношений, а не в динамике цен.

Куда же дальше?

Представленная работа, по сути, лишь намекает на возможность иного взгляда на привычные конструкции ликвидности. Модель, рассматривающая книгу ордеров как проявление геометрического сдвига в неком «до-порядке», — не столько объяснение, сколько приглашение к переосмыслению. Не стоит обольщаться, полагая, что удалось поймать за хвост саму причину асимметрии; скорее, обнаружен ещё один способ обмануть будущее, спроецировав на него желаемые паттерны.

Очевидным направлением дальнейших исследований представляется углубление в математический аппарат «гамма-геометрии». Однако, не стоит забывать, что любая модель — это лишь заклинание, работающее до первого контакта с реальными данными. Истинным вызовом является не построение более элегантной теории, а разработка способов её проверки, пусть даже и обречённых на неудачу. Ведь всё обучение — это акт веры, а метрика — лишь форма самоуспокоения.

Данные не врут, они просто помнят избирательно. И, возможно, именно в этой избирательности кроется ключ к пониманию того, как «до-порядок» порождает иллюзию предсказуемости. В конечном итоге, задача состоит не в том, чтобы предсказать будущее, а в том, чтобы научиться жить с его неопределённостью, принимая её как неотъемлемую часть самой реальности.

Оригинал статьи: https://arxiv.org/pdf/2601.19369.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-28 09:48