Хаос Винера на службе финансовых рынков

Автор: Денис Аветисян

Новая модель мартингального ценообразования, основанная на разложении по хаосу Винера, позволяет более точно калибровать опционные рынки и воспроизводить сложные динамики активов.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал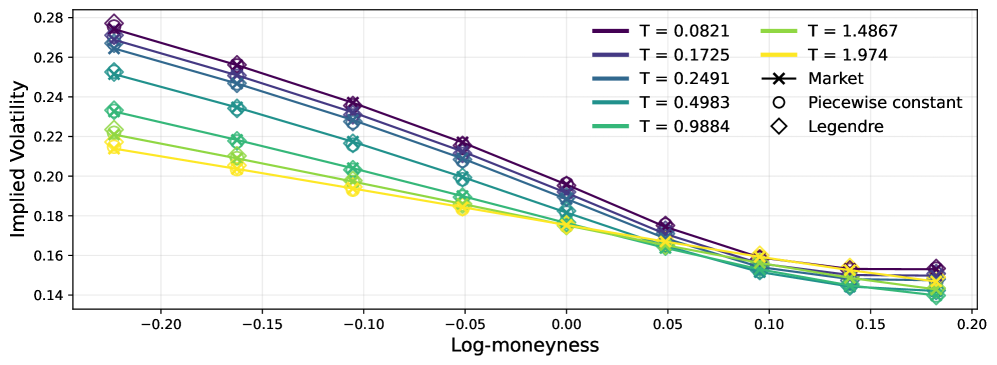

В рамках калибровки модели Хестона, построение поверхностей подразумеваемой волатильности с использованием кусочно-постоянной и базисов Лежандра демонстрирует, что кусочно-постоянный базис обеспечивает среднюю абсолютную ошибку в 7.23 базисных пункта, тогда как базис Лежандра - 8.80 базисных пункта, указывая на незначительное преимущество первого в точности аппроксимации рыночных данных. — В рамках калибровки модели Хестона, построение поверхностей подразумеваемой волатильности с использованием кусочно-постоянной и базисов Лежандра демонстрирует, что кусочно-постоянный базис обеспечивает среднюю абсолютную ошибку в 7.23 базисных пункта, тогда как базис Лежандра — 8.80 базисных пункта, указывая на незначительное преимущество первого в точности аппроксимации рыночных данных.

В статье представлен перепараметризованный мартингальный подход к моделированию финансовых активов с использованием разложения по хаосу Винера для калибровки и воспроизведения сложных рыночных условий.

Калибровка моделей к наблюдаемой поверхности опционных цен представляет собой сложную задачу, требующую гибкого описания динамики базового актива. В статье ‘A Wiener Chaos Approach to Martingale Modelling and Implied Volatility Calibration’ предложен новый, перепараметризованный мартингальный подход, основанный на разложении Винера, для моделирования динамики дисконтированной цены актива. Данный метод позволяет аппроксимировать терминальную стоимость мартингала посредством усеченного разложения по хаосу Винера, обеспечивая быструю калибровку к целевой поверхности подразумеваемой волатильности. Сможет ли предложенный подход эффективно улавливать сложные зависимости и улучшить точность прогнозирования на реальных рыночных данных?

Фундамент неопределенности: Представление риска через хаос Винера

Традиционные модели ценообразования опционов, несмотря на свою широкую распространенность, часто базируются на упрощающих предположениях, которые не отражают всей сложности реальной рыночной неопределенности. Например, предполагается нормальное распределение доходностей активов или постоянство волатильности, что далеко не всегда соответствует действительности. В результате, эти модели могут давать неточные оценки стоимости опционов, особенно в периоды повышенной рыночной турбулентности или при наличии экстремальных событий. Игнорирование «толстых хвостов» распределений и асимметрии доходностей приводит к недооценке рисков и, как следствие, к потенциальным убыткам для инвесторов. Поэтому возникает необходимость в более совершенных методах, способных адекватно учитывать все аспекты рыночной неопределенности и обеспечивать более надежные оценки стоимости опционов.

Расширение Винера представляет собой мощный математический аппарат для представления случайных величин в виде бесконечной суммы ортогональных полиномов. В отличие от традиционных подходов, которые часто ограничиваются упрощенными моделями, данная методика позволяет охватить более широкий спектр стохастических процессов и их сложное поведение. Каждый член этой суммы, построенный на основе ортогональных полиномов, описывает определенный уровень случайности, что дает возможность детально анализировать и моделировать неопределенность, присущую финансовым рынкам и другим областям, где случайные величины играют ключевую роль. Использование ортогональных полиномов гарантирует независимость этих компонентов, упрощая вычисления и интерпретацию результатов, что делает расширение Винера ценным инструментом в количественном анализе и управлении рисками.

В основе эффективного моделирования динамики цен активов лежит использование разложения Винера, в котором ключевую роль играют полиномы Эрмита. Данный подход позволяет представить случайные величины, описывающие изменения цен, в виде бесконечной суммы ортогональных полиномов $H_n(x)$ , что существенно расширяет возможности по учету сложных стохастических процессов. В отличие от традиционных моделей, полагающихся на упрощенные предположения о нормальности распределения, разложение Винера с полиномами Эрмита способно адекватно описывать нелинейные зависимости и учитывать асимметрию и эксцесс в распределении доходностей. Это, в свою очередь, позволяет создавать более точные и надежные модели ценообразования, учитывающие широкий спектр рыночных факторов и снижающие риски, связанные с упрощенными предположениями о поведении активов.

Сравнение опциона «Down-and-Out» показывает зависимость цены (верхний график) и подразумеваемой волатильности (нижний график) от времени.

Новый подход: Мартингальная модель хаоса Винера

Модель Винеровского Хаоса Мартингейла представляет собой инновационный подход к ценообразованию опционов, напрямую интегрирующий разложение Винеровского Хаоса в мартингальный фреймворк. В отличие от традиционных методов, использующих диффузионные процессы, данный подход позволяет представить ценовые процессы активов как сумму независимых случайных величин, определенных через полиномы Эрмита, что обеспечивает более гибкое моделирование динамики активов. Такая структура позволяет описывать сложные зависимости и нелинейности, присутствующие в реальных финансовых данных, за счет использования $H(\xi)$ — полиномов Винеровского Хаоса, где ξ — стандартный винеровский процесс. Интеграция в мартингальный фреймворк гарантирует отсутствие арбитражных возможностей и обеспечивает консистентность ценообразования.

Использование нейтрального к риску измерения (Risk Neutral Measure) является ключевым элементом в модели Wiener Chaos Martingale, позволяющим получить безрисковые цены опционов. Данный подход основан на построении вероятностного пространства, в котором ожидаемая доходность любого актива равна безрисковой ставке. В рамках этого измерения, цена опциона определяется как математическое ожидание дисконтированной выплаты по опциону, рассчитанное относительно нейтрального к риску распределения вероятностей. Это гарантирует отсутствие возможностей для арбитража, поскольку цена опциона отражает лишь компенсацию за риск, а не ожидаемую прибыль. Практическая реализация требует вычисления интеграла выплаты по опциону относительно нейтрального к риску измерения, что может быть выполнено с использованием численных методов, таких как квадратура.

Модель, в отличие от традиционных методов ценообразования опционов, обеспечивает повышенную гибкость в моделировании динамики цен активов. Это достигается за счет прямой интеграции разложения Винера в мартингальный фреймворк, что позволяет более точно отражать сложные характеристики рыночных процессов. Эффективная реализация модели осуществляется с использованием методов квадратур, что обеспечивает вычислительную эффективность. При калибровке к срокам погашения, модель демонстрирует среднюю абсолютную ошибку (MAE) в 6.75 базисных пунктов, подтверждая высокую точность и практическую применимость.

Сравнение форвардного колл-опциона демонстрирует зависимость цены и подразумеваемой волатильности, отражающую динамику изменения стоимости актива.

Повышение реалистичности: Стохастическая волатильность с Хестоном и за её пределами

Модель Хестона вносит значительное улучшение в традиционные предположения о постоянной волатильности, вводя понятие стохастической волатильности. В отличие от моделей, использующих фиксированное значение волатильности, модель Хестона предполагает, что волатильность сама по себе является случайным процессом, изменяющимся во времени. Это достигается путем моделирования волатильности как квадратного корня из случайного процесса, следующего логнормальному распределению. Такой подход позволяет более реалистично отражать поведение рынков, где волатильность не является постоянной, а подвержена флуктуациям и изменениям, что особенно важно при ценообразовании опционов и оценке рисков. $\sigma_t = \sqrt{V_t}$ , где $\sigma_t$ — волатильность в момент времени t, а $V_t$ — случайный процесс, определяющий ее динамику.

Для эффективной оценки опционов в рамках моделей Хестона и Шероховатого Хестона используется метод Монте-Карло. Этот подход позволяет учесть сложные динамики волатильности, которые невозможно адекватно смоделировать при использовании постоянной волатильности. Метод Монте-Карло заключается в генерации большого числа случайных траекторий базового актива и волатильности, и последующем вычислении среднего значения дисконтированной выплаты по опциону для этих траекторий. Благодаря своей гибкости, Монте-Карло позволяет точно оценить цены опционов даже при наличии сложных взаимосвязей между ценой актива и его волатильностью, что особенно важно для моделей, учитывающих стохастическую и шероховатую волатильность.

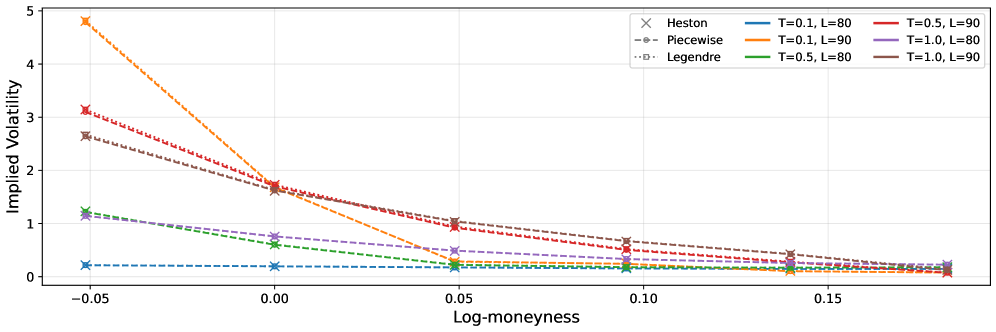
Модель Rough Heston расширяет возможности стохастической волатильности, добавляя параметр “шероховатости”, который позволяет учитывать долгосрочную зависимость в динамике волатильности. Это позволяет более точно моделировать сложные паттерны волатильности, наблюдаемые на финансовых рынках. При тестировании на опционах индекса SPX, модель продемонстрировала среднюю абсолютную ошибку (MAE) в 11.32 базисных пункта, что подтверждает ее высокую точность при работе с реальными рыночными данными и превосходит точность моделей, предполагающих постоянную волатильность или использующих только базовую стохастическую волатильность.

Модель rough Heston позволяет точно аппроксимировать подразумеваемую волатильность для краткосрочных опционов.

Широкое применение: Оценка экзотических опционов

Предложенные модели не ограничиваются лишь оценкой стоимости простых европейских опционов. Их универсальность позволяет успешно применять их к широкому спектру экзотических опционов, включая форвардные стартовые опционы, опционы с функцией lookback и опционы «down-and-out». В отличие от традиционных методов, данные модели способны учитывать сложные зависимости и характеристики этих инструментов, обеспечивая более точную и надежную оценку их справедливой стоимости. Это расширение возможностей особенно ценно для финансовых институтов и трейдеров, работающих с более сложными производными финансовыми инструментами, и позволяет им оптимизировать стратегии управления рисками и максимизировать потенциальную прибыль.

Модели, описанные ранее, не ограничиваются ценообразованием стандартных европейских опционов, а позволяют с повышенной точностью оценивать стоимость и более сложных финансовых инструментов. К таким инструментам относятся форвард-стартующие опционы, которые активируются в будущем, опционы с функцией «lookback», позволяющие зафиксировать наилучшую цену за определенный период, и «down-and-out» опционы, прекращающие свое действие при достижении определенного уровня цены. Использование предложенных методов позволяет более адекватно учитывать различные факторы риска, присущие этим сложным производным финансовым инструментам, и, как следствие, получать более точные оценки их справедливой стоимости. Это особенно важно для инвесторов и трейдеров, работающих с экзотическими опционами, поскольку даже небольшие погрешности в ценообразовании могут привести к существенным финансовым потерям.

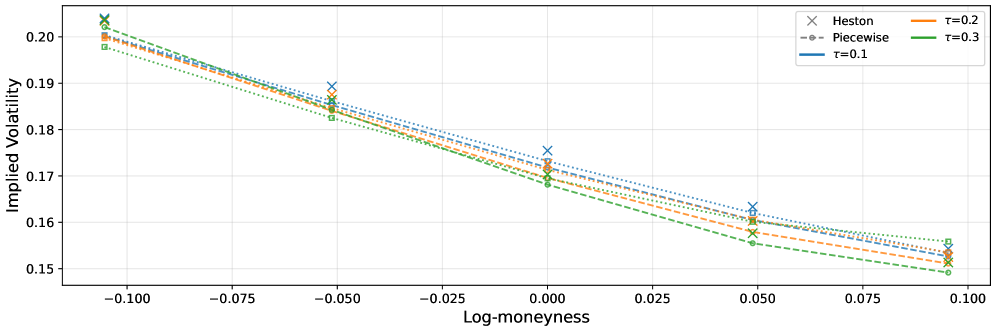
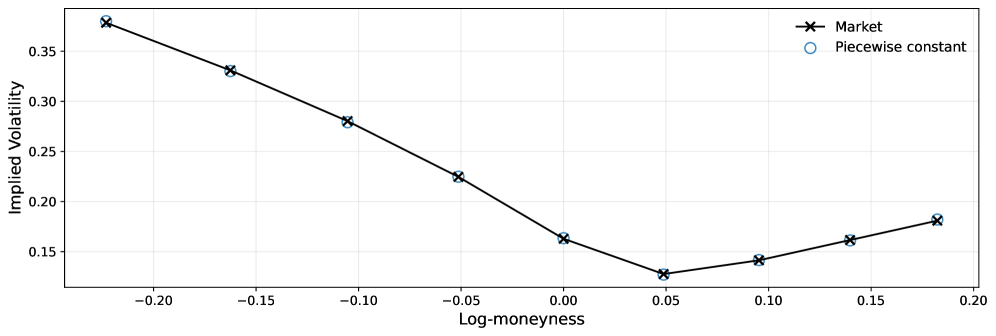
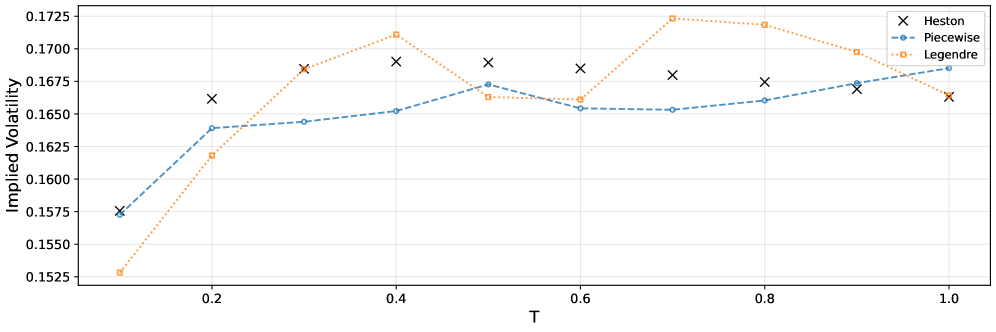
Разработанные модели позволяют существенно повысить точность расчета подразумеваемой волатильности — ключевого показателя для участников рынка, используемого в оценке рисков и формировании стратегий. Проведенная калибровка моделей на основе опционов SPX продемонстрировала впечатляющую эффективность: время калибровки составило всего 60 секунд, что свидетельствует о высокой скорости и практической применимости представленного подхода. Это позволяет трейдерам и аналитикам оперативно оценивать рыночные условия и принимать обоснованные решения, основанные на более точных данных о волатильности активов.

Сравнение опционов колл с плавающим страйком и lookback показывает зависимость цены и подразумеваемой волатильности от времени.

Исследование, представленное в данной работе, демонстрирует, как сложные финансовые модели могут быть построены на основе разложения Винера, позволяя точно калибровать динамику активов и соответствовать рыночным данным. Этот подход, по сути, признает, что каждая архитектура проживает свою жизнь, и стремится уловить ее эволюцию. Юрген Хабермас однажды заметил: «Коммуникативное действие — это поведение, ориентированное на достижение взаимопонимания». Аналогично, данная модель стремится к взаимопониманию между теоретической моделью и реальными рыночными данными, используя стохастическую волатильность и методы Монте-Карло для достижения этой цели. Подобные системы стареют, но представленная методология демонстрирует потенциал для адаптации и поддержания актуальности в постоянно меняющемся финансовом ландшафте.

Что дальше?

Представленная работа, хотя и демонстрирует элегантность подхода Винера к моделированию мартингалов и калибровке неявной волатильности, не является, разумеется, финальной нотой. Скорее, это — очередной поворот в бесконечном диалоге с неопределенностью. Каждый успешный сбой в калибровке, каждое отклонение от идеальной симуляции — сигнал времени, напоминание о том, что любая модель — это лишь приближение, а не отражение абсолютной истины. Истинная сложность финансовых систем, вероятно, потребует не просто более изощренных математических инструментов, но и переосмысления самой концепции «рынка».

Необходимо признать, что предложенная перепараметризация, хоть и эффективна в решении конкретной задачи, несет в себе и потенциальные риски. Рефакторинг модели — это всегда диалог с прошлым, попытка извлечь уроки из ошибок и ограничений. Важно, чтобы стремление к увеличению точности не приводило к потере интерпретируемости и управляемости модели. Иначе, словно строя великолепный собор на зыбучих песках, можно лишь ускорить неизбежное.

В перспективе представляется плодотворным исследование возможности применения данного подхода к более широкому классу активов и рынков, а также разработка методов адаптивной калибровки, позволяющих учитывать изменяющуюся динамику волатильности. В конечном счете, вопрос не в том, насколько точно можно предсказать будущее, а в том, насколько достойно система реагирует на его наступление.

Оригинал статьи: https://arxiv.org/pdf/2602.16232.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-19 08:49