Игры с неопределенностью: вычисление равновесий при случайных ограничениях

Автор: Денис Аветисян

Новое исследование предлагает эффективные алгоритмы для поиска равновесий Нэша в играх, где доступные действия игроков меняются случайным образом.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал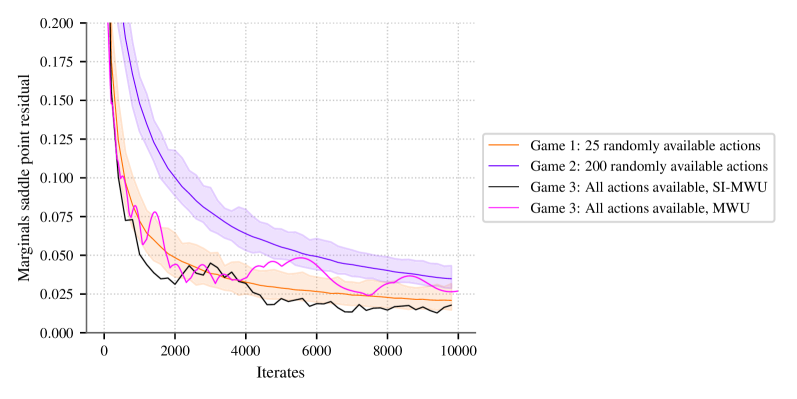

В исследовании сравниваются остатки седловых точек маргинального распределения, полученные алгоритмом SI-MWU, в серии из 100 случайных игр 25x200 и 200x25, где у игроков с 25 или 200 действиями представлены стохастические множества действий, а также нестохастическая игра с той же матрицей выигрышей, решенная как SI-MWU, так и стандартным MWU, что демонстрирует средние значения и 95% центральный интервал для оценки стабильности и точности алгоритмов. — В исследовании сравниваются остатки седловых точек маргинального распределения, полученные алгоритмом SI-MWU, в серии из 100 случайных игр 25×200 и 200×25, где у игроков с 25 или 200 действиями представлены стохастические множества действий, а также нестохастическая игра с той же матрицей выигрышей, решенная как SI-MWU, так и стандартным MWU, что демонстрирует средние значения и 95% центральный интервал для оценки стабильности и точности алгоритмов.

Представлен фреймворк для анализа и вычисления приближенных равновесий в играх с вероятностными наборами действий, использующий компактное представление стратегий и методы минимизации сожаления.

В традиционном анализе игр часто предполагается полный доступ игроков ко всем возможным действиям, однако на практике это ограничение не всегда применимо. В работе ‘Computing Equilibria in Games with Stochastic Action Sets’ предложен новый подход к моделированию игр, в которых набор доступных действий каждого игрока подвержен случайным ограничениям, вводится понятие игры со стохастическим набором действий (GSAS). Показано, что в GSAS равновесия Нэша могут быть компактно представлены вектором размера $\vert A_i\vert$ , что позволяет разработать эффективный алгоритм вычисления приближенных равновесий со скоростью сходимости $O(\sqrt{\log\vert A_i\vert/T})$ . Каковы перспективы применения данного подхода к анализу более сложных игровых сценариев с неполной информацией и динамически меняющимися ограничениями?

Вызов стохастических сред

Традиционная теория игр, как правило, опирается на предположение о полной доступности информации и одновременном выполнении действий всеми участниками. Однако, такое упрощение не отражает реальность многих ситуаций, где вероятность успешного выполнения действия может быть неопределенной или зависеть от внешних факторов. Например, в задачах распределения ресурсов или обеспечения сетевой безопасности, попытки вмешательства могут оказаться неудачными из-за технических сбоев или преднамеренных действий противника. Игнорирование вероятностного характера доступных действий приводит к нереалистичным моделям и неэффективным стратегиям, что ограничивает применимость классической теории игр в динамичных и непредсказуемых средах. В подобных условиях, необходимо учитывать, что не каждое запланированное действие гарантированно принесет ожидаемый результат, и стратегии должны быть разработаны с учетом этой неопределенности.

Ограничения традиционной теории игр становятся особенно заметными в реальных сценариях, таких как распределение ресурсов или обеспечение сетевой безопасности. В этих областях действия часто не гарантированы: попытка доступа к ресурсу может оказаться неудачной из-за конкуренции, сетевая атака может быть заблокирована системой защиты, а передача данных — задержана из-за перегрузки сети. Невозможность предвидеть успех каждой отдельной операции требует от стратегий адаптивности и учета вероятности провала или задержки, что делает классические модели неэффективными для анализа и прогнозирования поведения в подобных динамичных и неопределенных средах. Таким образом, необходим новый подход к разработке стратегий, учитывающий вероятностный характер доступных действий и позволяющий оптимизировать решения в условиях риска и неопределенности.

Игры со стохастическими множествами действий (GSAS) представляют собой более реалистичную модель многих реальных ситуаций, где доступность того или иного действия не гарантирована, а определяется вероятностью. В отличие от классической теории игр, предполагающей полную информацию и детерминированные действия, GSAS учитывают возможность сбоев, задержек или просто случайного характера выбора. Однако, это усложнение порождает новые трудности при поиске стабильных равновесий. Традиционные методы анализа игр могут оказаться неэффективными, поскольку игрокам приходится учитывать не только стратегии оппонентов, но и вероятности успешной реализации собственных действий. Разработка алгоритмов и концепций, способных эффективно анализировать GSAS и находить надежные решения, является актуальной задачей современной теории игр и имеет важное практическое значение для таких областей, как распределение ресурсов, кибербезопасность и управление рисками.

Решение случайно сгенерированных задач GSAS алгоритмом SI-MWU демонстрирует сравнимое с Gurobi время работы, при этом среднее время для 20 запусков показано линией, а диапазон значений - затенённой областью. — Решение случайно сгенерированных задач GSAS алгоритмом SI-MWU демонстрирует сравнимое с Gurobi время работы, при этом среднее время для 20 запусков показано линией, а диапазон значений — затенённой областью.

Определение сожаления в стохастическом мире

Стандартные определения сожаления (regret) не применимы к играм с исчезающими и появляющимися действиями (GSAS), поскольку они наказывают игрока за невыбор действий, которые в данный момент времени просто недоступны. Традиционное вычисление сожаления предполагает, что игрок всегда имеет возможность выбрать любое действие, и оценивает упущенную выгоду от альтернативных вариантов. В GSAS, когда набор доступных действий меняется случайным образом, наказание за невыбор недоступного действия искажает реальную оценку эффективности стратегии игрока и приводит к неверным выводам о его производительности. Это особенно важно, поскольку стандартные алгоритмы оптимизации, основанные на минимизации сожаления, будут ошибочно стремиться к выбору недоступных действий, что делает их непригодными для использования в динамических игровых средах.

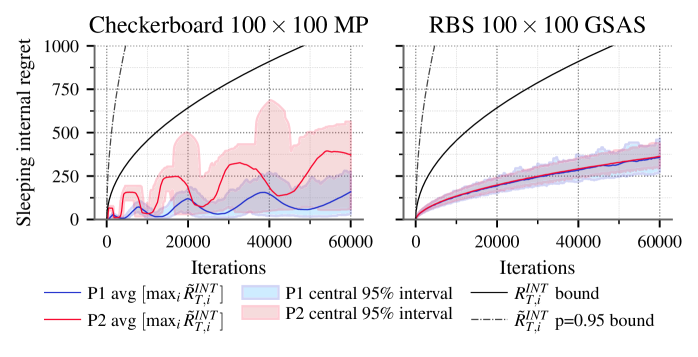
В контексте анализа сожаления в стохастических игровых средах, таких как GSAS, традиционные определения сожаления часто неадекватны, поскольку учитывают сожаление по действиям, которые были недоступны в данный момент времени. В отличие от этого, «внутреннее сожаление о спящих действиях» (SI-Сожаление) представляет собой уточненную метрику, которая фокусируется исключительно на сожалении, связанном с действиями, которые могли быть выполнены игроком. Это означает, что при расчете сожаления учитываются только те действия, которые были доступны в конкретной игровой ситуации, что позволяет более точно оценить эффективность стратегии игрока и избежать необоснованной критики за невозможность выбора недоступных опций. Формально, SI-Сожаление оценивает разницу между вознаграждением, полученным игроком, и максимальным вознаграждением, которое он мог бы получить, выбрав лучшее доступное действие в каждый момент времени.

Определение SI-Regret основывается на концепциях, разработанных в рамках задачи о «Спящем Разбойнике» (Sleeping Bandit problem). В этой задаче, действия (разбойники) появляются и исчезают случайным образом во времени, что требует от агента адаптировать свою стратегию выбора действий к меняющейся доступности. Математически, задача моделируется как последовательность раундов, где в каждом раунде появляется подмножество доступных действий, выбранных из общего набора. Использование принципов, разработанных для решения задачи о «Спящем Разбойнике», позволяет построить теоретически обоснованную метрику сожаления (regret) для GSAS, учитывающую только те действия, которые были доступны в конкретный момент времени и не наказывая игрока за невозможность выбора недоступных вариантов. Это обеспечивает более корректную оценку эффективности стратегии в условиях стохастической доступности действий.

Анализ внутренних сожалений SI-MWU для нескольких 2p0s-GSAS показал, что среднее значение [latex]\max_{i}\tilde{R}_{T,i}^{INT}[/latex] и [latex]\max_{i}\tilde{R}_{T,I}^{INT}[/latex] ограничены теоремой 4.4 и пропозицией 4.5 соответственно, что подтверждается центральным 95% интервалом, полученным в результате 100 повторений каждого эксперимента. — Анализ внутренних сожалений SI-MWU для нескольких 2p0s-GSAS показал, что среднее значение $\max_{i}\tilde{R}_{T,i}^{INT}$ и $\max_{i}\tilde{R}_{T,I}^{INT}$ ограничены теоремой 4.4 и пропозицией 4.5 соответственно, что подтверждается центральным 95% интервалом, полученным в результате 100 повторений каждого эксперимента.

SI-MWU: Сходящийся алгоритм обучения

Алгоритм SI-MWU использует концепцию SI-Регрета (Self-Improvement Regret) для итеративного обновления стратегий в контексте GSAS (General Stochastic Approximation Strategies). SI-Регрет представляет собой меру упущенной выгоды от использования альтернативной стратегии в прошлом, учитывая наблюдаемые результаты. Минимизируя SI-Регрет на каждой итерации, алгоритм направлен на приближение к равновесию Нэша — состоянию, в котором ни один игрок не может улучшить свою выгоду, односторонне изменив свою стратегию. Этот подход позволяет алгоритму адаптироваться к изменяющимся условиям и приближаться к оптимальному решению в стохастических играх, где исходы действий непредсказуемы.

Алгоритм SI-MWU использует методы стохастической аппроксимации для обработки зашумленных оценок, возникающих в стохастических средах. Эти методы позволяют получать последовательные приближения к оптимальным стратегиям, несмотря на случайную природу обратной связи и неопределенность в оценках выигрышей. В частности, стохастическая аппроксимация применяется для оценки ожидаемых выигрышей от различных действий, используя средние значения, полученные на основе выборочных данных. Это особенно важно в ситуациях, когда точное вычисление ожидаемых выигрышей невозможно или вычислительно затратно, поскольку алгоритм адаптируется к имеющимся неточным данным, стремясь к стабильному решению.

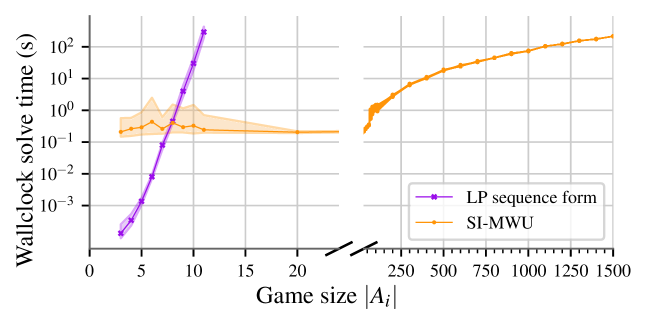
Алгоритм SI-MWU гарантирует сходимость к стабильному профилю стратегий за счет минимизации SI-Регрета, даже в условиях вероятностной доступности действий. В работе показано, что SI-MWU масштабируется для решения игр большего размера, чем стандартные решатели, такие как Gurobi. Это достигается за счет использования стохастических приближений, позволяющих эффективно обрабатывать шумы, возникающие при оценке стратегий в стохастических средах, и итеративного обновления стратегий на основе SI-Регрета. Таким образом, SI-MWU предоставляет возможность анализа более сложных игровых сценариев, недоступных для традиционных методов.

Эмпирические результаты демонстрируют, что алгоритм SI-MWU достигает сублинейного сожаления с высокой вероятностью. На практике, это означает, что среднее сожаление алгоритма снижается пропорционально $O(1/\sqrt{T})$ , где $T$ — число сыгранных раундов. Подтверждено соответствие наблюдаемых результатов теоретически установленным границам, что указывает на корректность математической модели и эффективности алгоритма в различных тестовых сценариях. Статистический анализ показывает, что вероятность превышения теоретических границ сожаления крайне мала, что подтверждает надежность и предсказуемость работы SI-MWU.

Анализ остатков седловой точки [latex]w_{i}^{t}[/latex], полученных для различных стратегий 2p0s-GSAS с использованием SI-MWU, показывает, что усреднение по 100 повторениям эксперимента и отбрасывание первых 500 маржинальных распределений обеспечивает стабильность стохастической аппроксимации. — Анализ остатков седловой точки $w_{i}^{t}$ , полученных для различных стратегий 2p0s-GSAS с использованием SI-MWU, показывает, что усреднение по 100 повторениям эксперимента и отбрасывание первых 500 маржинальных распределений обеспечивает стабильность стохастической аппроксимации.

Влияние на разработку надежных стратегий

Метод SI-MWU представляет собой структурированный подход к разработке устойчивых стратегий, способных эффективно функционировать в условиях неопределенности и вероятности сбоев в действиях. В его основе лежит способность адаптироваться к изменяющимся обстоятельствам и минимизировать негативные последствия от непредсказуемых событий. В отличие от традиционных методов, SI-MWU не требует точного знания вероятностей различных исходов, а полагается на анализ прошлых данных и прогнозирование будущих тенденций. Этот подход позволяет создавать стратегии, которые остаются эффективными даже при возникновении неожиданных препятствий или ошибок, обеспечивая надежность и стабильность в сложных и динамичных системах. Использование SI-MWU позволяет учитывать широкий спектр рисков и разрабатывать планы действий, которые минимизируют потери и максимизируют возможности для достижения поставленных целей, что особенно важно в условиях высокой конкуренции и быстро меняющегося мира.

Концепция SI-Регрета, изначально разработанная для анализа стратегий в контексте GSAS (Game-theoretic Stochastic Approximation of Signaling), оказалась применимой и в более широком спектре стохастических сред. Данный показатель позволяет оценить накопленную «стоимость упущенных возможностей» в процессе обучения стратегии, учитывая не только текущие потери, но и потенциальные выгоды от альтернативных действий в условиях неопределенности. В отличие от традиционных мер сожаления, SI-Регрет учитывает вероятностный характер как действий игрока, так и окружающей среды, что делает его особенно ценным при анализе сложных систем, где случайные факторы играют значительную роль. Применение SI-Регрета позволяет более точно оценивать эффективность стратегий в различных областях, от экономики и финансов до робототехники и машинного обучения, предоставляя инструмент для разработки более устойчивых и адаптивных решений.

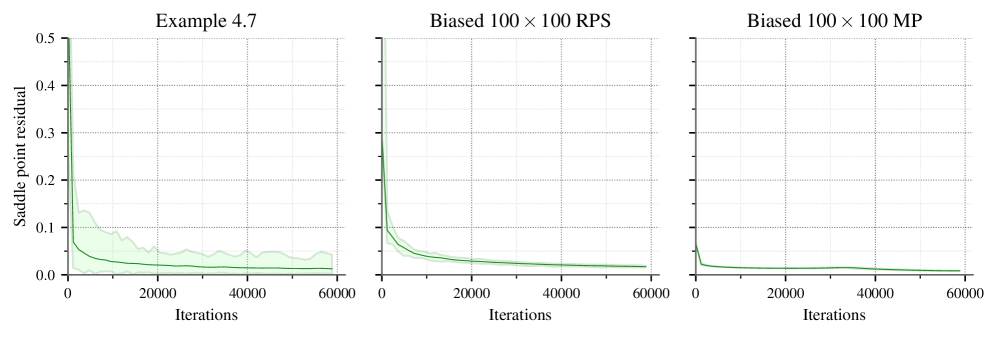
Несмотря на то, что далеко не все игровые ситуации являются строго соревновательными (с нулевой суммой), принципы обучения без сожалений, в сочетании с концепцией SI-Сожаления, способны приводить к стабильным результатам в широком спектре сценариев. Этот подход позволяет находить приближенные равновесия Нэша, характеризующиеся низким остатком седловой точки $Saddle-Point Residual$ . Низкий остаток указывает на устойчивость стратегий, поскольку отклонение от равновесия не приносит существенной выгоды ни одному из игроков. Таким образом, даже в кооперативных или смешанных игровых ситуациях, применение SI-Регрета в рамках обучения без сожалений способствует формированию предсказуемых и устойчивых стратегий, обеспечивая стабильность системы в условиях неопределенности и возможных ошибок действий.

Эксперименты с использованием SI-MWU для различных 2p0s-GSAS демонстрируют, что среднее значение SI-регрета соответствует теоретическим границам, как показано на центральном 95% интервале, полученном из 100 повторений каждого типа игры.

За пределами равновесия Нэша: к масштабируемым игровым решениям

Разработанный алгоритм SI-MWU, в сочетании с методами линейного программирования для проверки равновесия Нэша, представляет собой перспективный подход к решению сложных игр, включающих элементы случайности. Такой симбиоз позволяет не только находить приближенные решения в играх с высокой степенью неопределенности, но и верифицировать их оптимальность, используя строгие математические критерии. В отличие от традиционных методов, SI-MWU демонстрирует потенциал для масштабирования и эффективного анализа игр, где количество игроков и доступных действий может быть весьма велико. $\nabla f(x)$ Этот подход открывает новые возможности для моделирования и анализа широкого спектра реальных задач, от экономики и финансов до теории игр и искусственного интеллекта, предоставляя инструменты для принятия оптимальных решений в условиях риска и неопределенности.

Перспективные исследования направлены на повышение масштабируемости алгоритма SI-MWU для решения игр с большим числом участников и возможных действий. В настоящее время, практическое применение данного метода сталкивается с вычислительными сложностями при увеличении размерности игрового пространства. Ученые работают над оптимизацией алгоритма, используя методы параллельных вычислений и приближенные решения, чтобы снизить потребность в вычислительных ресурсах. Успешная реализация этих улучшений позволит применять SI-MWU для анализа сложных экономических моделей, стратегий в сетевых играх и других задач, где количество игроков и доступных действий существенно влияет на результаты. Дальнейшая работа предполагает исследование возможности адаптации алгоритма к динамически изменяющимся игровым средам и разработку методов эффективной оценки качества приближенных решений.

Более глубокое изучение остатка в седловой точке $Saddle-Point Residual$ представляется ключевым для оценки устойчивости и сходимости алгоритма. Этот остаток, по сути, отражает степень отклонения текущего решения от истинной седловой точки, представляющей собой равновесие в игре. Анализ его динамики в процессе итераций позволяет не только прогнозировать скорость сходимости алгоритма к оптимальному решению, но и выявлять потенциальные проблемы, такие как осцилляции или замедление сходимости вблизи седловой точки. В частности, понимание взаимосвязи между величиной остатка и параметрами игры, а также разработка методов его эффективного снижения, способствуют повышению надежности и точности алгоритма при решении сложных игровых сценариев, особенно в условиях высокой неопределенности и большого количества участников.

Анализ остатков седловой точки маргинального распределения, полученного с помощью SI-MWU для различных 2p0s-GSAS, показывает стабильность алгоритма, о чем свидетельствует незначительный разброс (диапазон) средних значений, рассчитанных по 100 повторениям каждого эксперимента.

Исследование равновесий в играх со случайными наборами действий демонстрирует, что даже в условиях неопределенности и ограниченных возможностей игроков, системы стремятся к стабильному состоянию. Авторы предлагают алгоритмы для эффективного представления и вычисления приближенных равновесий, подчеркивая важность компактного представления стратегий. Как однажды заметил Дональд Дэвис: «Простота — это высшая степень утонченности». Эта мысль находит отражение в подходе, предложенном в статье, где элегантность и ясность структуры позволяют находить решения даже в сложных игровых сценариях, где каждый игрок сталкивается с ограничениями в своих действиях. Устойчивость системы, как и в живом организме, зависит от четко определенных границ и эффективной организации.

Куда Далее?

Представленная работа, анализируя равновесия в играх со стохастическими множествами действий, лишь аккуратно приоткрывает дверь в сложный ландшафт. Эффективное представление стратегий, особенно в условиях растущей сложности, остается нетривиальной задачей. Текущие алгоритмы, хотя и демонстрируют сходимость к приближенным равновесиям, все еще сталкиваются с ограничениями в масштабируемости и вычислительной эффективности, напоминая о необходимости дальнейшей оптимизации. Инфраструктура должна развиваться без необходимости перестраивать весь квартал — поэтому будущее, вероятно, лежит в разработке более модульных и адаптивных подходов.

Особый интерес представляет изучение связи между стохастичностью множеств действий и робастностью равновесий. Насколько незначительные изменения в структуре игры влияют на стабильность найденных решений? Разработка алгоритмов, способных не только находить равновесия, но и оценивать их устойчивость к возмущениям, представляется ключевым направлением. В конечном счете, структура определяет поведение, и понимание этой взаимосвязи позволит создавать более надежные и предсказуемые игровые модели.

Нельзя игнорировать и потенциал применения этих результатов в смежных областях, таких как многоагентное обучение с подкреплением и проектирование автономных систем. Однако, прежде чем говорить о практической реализации, необходимо преодолеть ряд теоретических препятствий, касающихся, в частности, гарантий сходимости и оценки качества приближенных решений. Элегантный дизайн рождается из простоты и ясности, а значит, упрощение и обобщение существующих моделей — залог дальнейшего прогресса.

Оригинал статьи: https://arxiv.org/pdf/2602.16234.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-19 12:10