Игры со множеством агентов: как учесть риски и неидеальную рациональность

Автор: Денис Аветисян

Новая модель MF-RQE позволяет анализировать поведение больших групп агентов, учитывая их нежелание к риску и ограниченную способность к оптимальному принятию решений.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал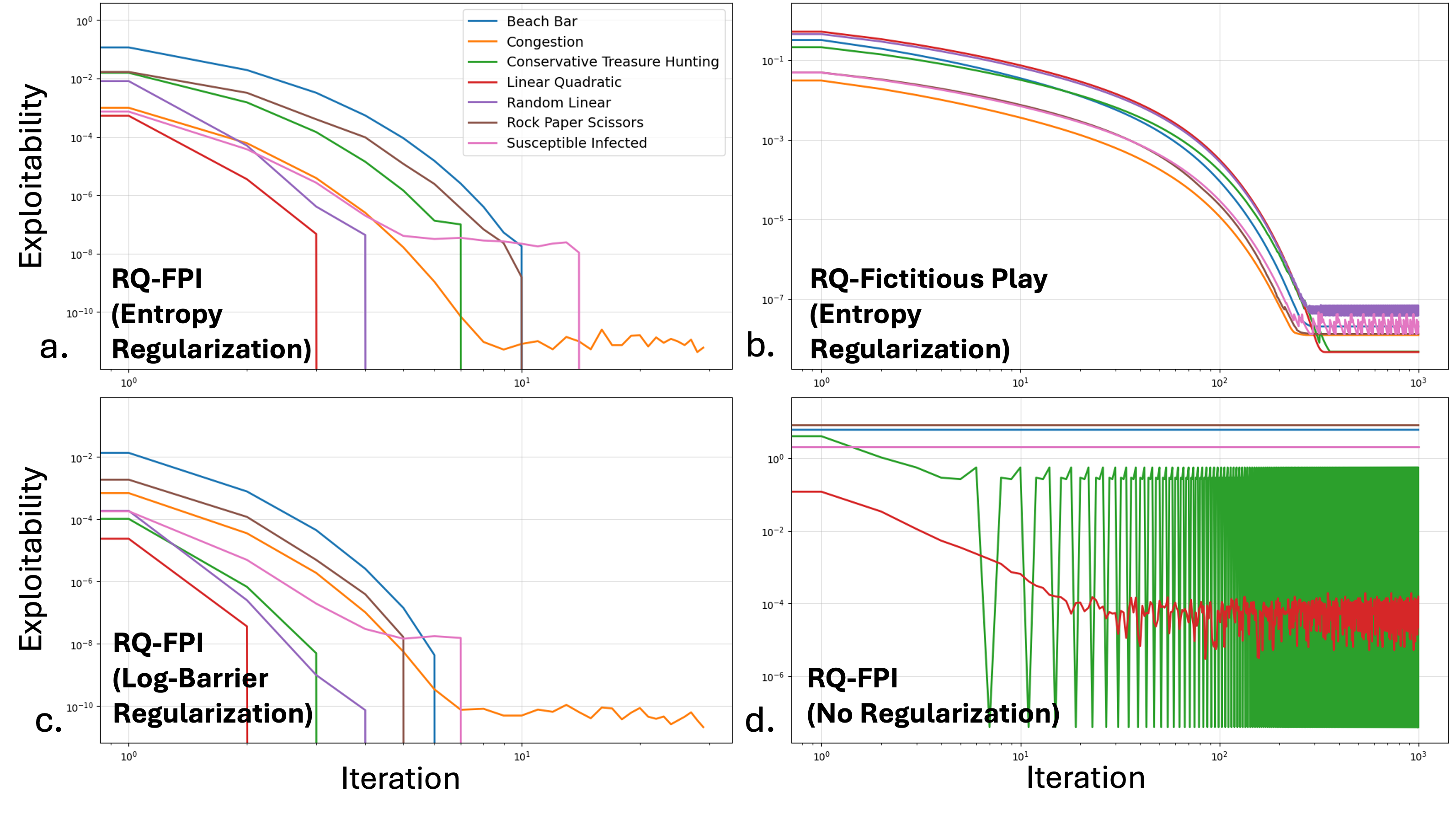

В контексте задач о средних полях, алгоритм RQ-FPI, в сочетании с различными методами регуляризации, демонстрирует сходимость к неэксплуатируемой политике MF-RQE, при этом учет риска позволяет достичь устойчивости к неопределенностям в начальных распределениях, хотя и с умеренким снижением ожидаемой доходности, что подтверждается результатами, полученными в моделях SIS и для транспортной игры с четырьмя состояниями, а также в дополнительных средах MFGLib, где даже переход от энтропийной регуляризации к логарифмическому барьеру не меняет общую тенденцию, подчеркивая важность ограниченной рациональности для достижения как вычислительной эффективности, так и сходимости.

Предложена новая структура для анализа игр со средним полем, включающая неприятие риска и ограниченную рациональность агентов.

Несмотря на успехи в теории игр со средним полем, существующие модели часто опираются на упрощающие предположения о полной рациональности агентов и фиксированном начальном распределении популяции. В работе ‘Robust Mean-Field Games with Risk Aversion and Bounded Rationality’ предложен новый подход, учитывающий неприятие риска по отношению к начальному распределению и ограниченную рациональность агентов. Вводится концепция равновесия MF-RQE (Mean-Field Risk-Averse Quantal Response Equilibrium), для которого доказаны условия существования и сходимости и разработан масштабируемый алгоритм обучения с подкреплением. Позволит ли предложенный подход создавать более устойчивые и реалистичные модели многоагентных систем в условиях неопределенности и когнитивных ограничений?

Ограничения Традиционных Многоагентных Систем: К Сути Проблемы

Классическая теория игр, венец которой — концепция равновесия Нэша, традиционно предполагает абсолютную рациональность агентов и полное знание о состоянии системы. Однако, в реальных сложных системах эти предположения часто не соответствуют действительности. Агенты, будь то люди, животные или искусственные интеллекты, редко обладают полной информацией или способностью просчитывать все возможные последствия своих действий. Предположение о совершенной рациональности игнорирует когнитивные ограничения, эвристики и поведенческие особенности, которые влияют на принятие решений. В результате, применение строгих математических моделей, основанных на равновесии Нэша, может приводить к неточным прогнозам и неоптимальным стратегиям в условиях неопределенности и неполной информации, что ограничивает их применимость в моделировании реальных многоагентных систем.

Существующие многоагентные системы часто сталкиваются с трудностями при моделировании поведения агентов, обладающих ограниченной рациональностью или склонных к избеганию рисков. В отличие от теоретических моделей, предполагающих абсолютную рациональность и полную осведомленность, реальные агенты принимают решения на основе неполной информации и с учетом когнитивных ограничений. Это приводит к тому, что агенты не всегда выбирают оптимальные стратегии, даже если теоретически доступны. Стремление к избеганию рисков, в свою очередь, может заставить агентов отказываться от потенциально выгодных, но сопряженных с неопределенностью, возможностей. В результате, общая эффективность системы снижается, и наблюдаются отклонения от теоретически достижимых результатов. Игнорирование этих факторов в существующих подходах ограничивает их применимость в сложных и непредсказуемых сценариях.

Ограничения традиционных многоагентных систем особенно проявляются при работе с большими популяциями и неопределенностью начальных условий. В подобных сценариях, где количество взаимодействующих агентов велико, а исходная информация неполна или содержит ошибки, классические методы оптимизации часто дают результаты, существенно отличающиеся от оптимальных. Это связано с тем, что даже незначительные отклонения в начальных данных могут экспоненциально усиливаться при увеличении числа агентов, приводя к непредсказуемым и неэффективным решениям. В результате, традиционные подходы, основанные на предположении о полной рациональности и информации, оказываются неприменимыми к моделированию реальных, сложных систем, требуя разработки новых методов, учитывающих неизбежную неопределенность и ограниченность ресурсов агентов.

MF-RQE: Новая Концепция Равновесия, Основанная на Среднем Поле

Модель MF-RQE базируется на принципах теории среднего поля (Mean Field Theory), что позволяет анализировать системы с большим числом агентов, фокусируясь на их совокупном поведении. Вместо анализа индивидуальных действий каждого агента, MF-RQE рассматривает усредненное поведение популяции, описываемое посредством $\mathbb{E}[x_i(t)]$ , где $x_i(t)$ — состояние i-го агента в момент времени t. Такой подход значительно упрощает вычислительную сложность, делая возможным получение аналитических решений для задач, которые были бы неразрешимы при детальном моделировании каждого агента. Это особенно важно при изучении динамических систем, где необходимо оценить влияние большого числа взаимодействующих элементов.

В отличие от традиционных подходов теории среднего поля, MF-RQE (Mean-Field Risk-Aversion & Bounded Rationality Equilibrium) явно учитывает неприятие риска агентами и их ограниченную рациональность в процессе поиска решения. Это достигается путем включения параметров, отражающих индивидуальные предпочтения к риску и когнитивные ограничения в модели принятия решений каждого агента. В результате, MF-RQE демонстрирует устойчивость к неопределенности начального распределения, что подтверждается основными результатами исследования и обеспечивает более надежные прогнозы поведения системы в условиях неполной информации. Учет этих факторов позволяет более реалистично моделировать поведение больших популяций агентов и получать решения, менее чувствительные к незначительным изменениям в исходных данных.

Предлагаемый подход расширяет существующие $MeanFieldGames$ за счет более детализированного моделирования процесса принятия решений агентами. В отличие от стандартных моделей, которые часто предполагают полное рациональное поведение и знание о функциях выигрыша других игроков, данная структура учитывает ограниченную рациональность агентов и неполноту информации. Это достигается за счет включения в модель параметров, описывающих степень риска-отвращения и когнитивные ограничения агентов, что позволяет получить более реалистичные прогнозы поведения в сложных системах с большим количеством взаимодействующих участников. Такой подход позволяет учитывать, что агенты не всегда стремятся к глобальному оптимуму, а принимают решения, основываясь на доступной информации и индивидуальных предпочтениях.

Результаты сходимости алгоритма D-RQ-FPI с энтропийной регуляризацией демонстрируют его эффективность как в сценарии SIS, так и в сценарии перегрузки.

Вычислительная Реализация и Валидация Метода MF-RQE

Процесс решения MF-RQE (Mean-Field Reinforcement Learning with Quadratic Error) опирается на методы $ConvexOptimization$ , что обеспечивает эффективное и надежное вычисление оптимальных стратегий. Использование алгоритмов выпуклой оптимизации гарантирует сходимость к глобальному минимуму целевой функции, что критически важно для задач с большим числом агентов и сложными динамическими моделями. Данный подход позволяет решать задачи MF-RQE за приемлемое время, даже при высокой размерности пространства состояний и действий, за счет использования специализированных алгоритмов и структур данных, оптимизированных для выпуклых задач. Эффективность и надежность методов $ConvexOptimization$ подтверждается результатами численных экспериментов, представленных в следующих разделах.

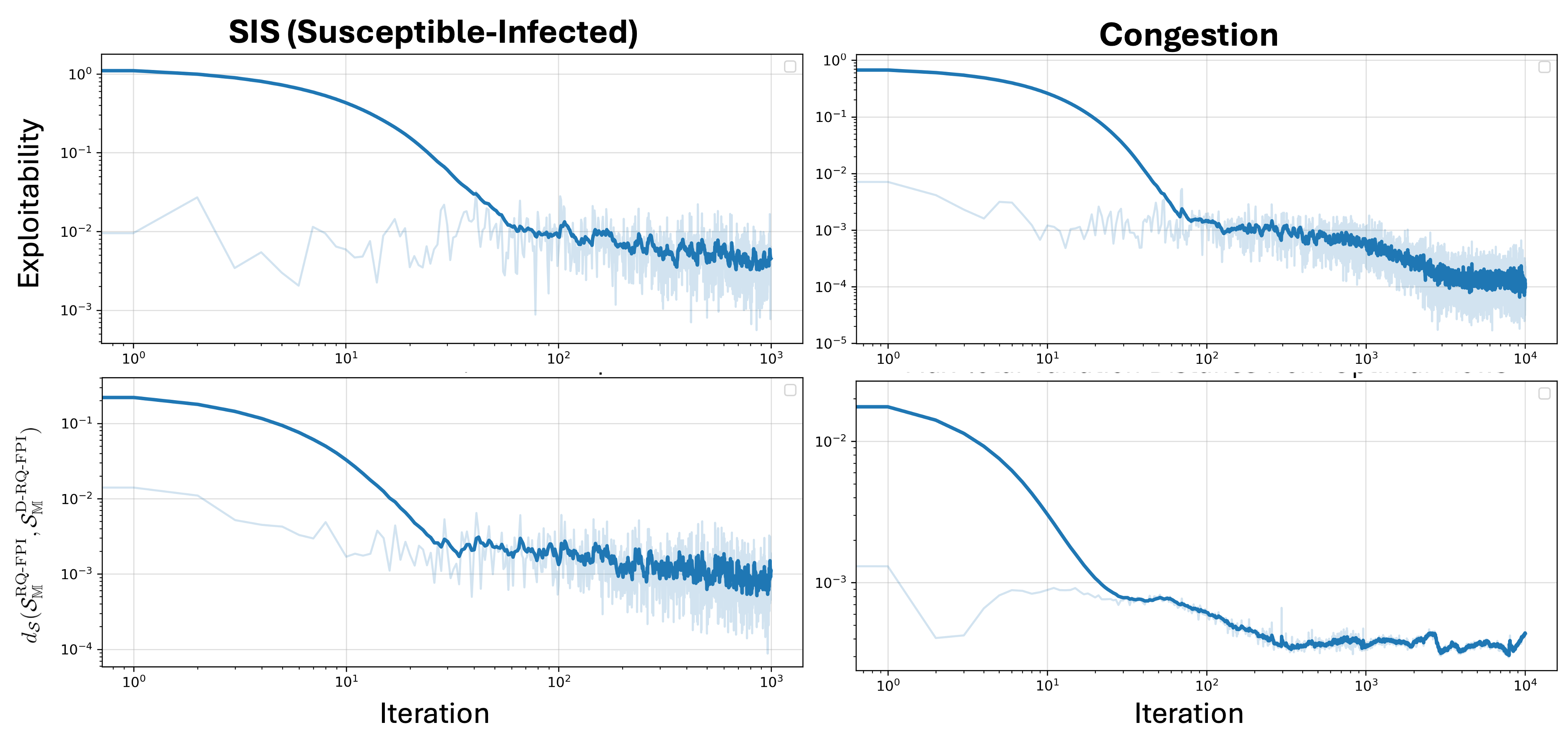
Для решения задачи MF-RQE (Mean-Field Reinforcement Learning with Quadratic Error) используются как настройки, основанные на моделе ( $ModelBasedSettings$ ), так и настройки, основанные на выборках ( $SampleBasedSettings$ ). $ModelBasedSettings$ применяются в случаях, когда доступна полная модель динамики системы, позволяя осуществлять точное вычисление оптимальных стратегий. $SampleBasedSettings$ , напротив, позволяют решать задачу, используя лишь данные, полученные в результате моделирования или экспериментов, что особенно полезно при работе со сложными системами, для которых построение точной модели затруднительно или невозможно. Комбинирование этих двух подходов обеспечивает гибкость и адаптируемость алгоритма к различным структурам решаемых задач и позволяет эффективно использовать доступные данные.

Разработанные методы позволяют проводить анализ сценариев, в которых агенты взаимодействуют в рамках управления средним полем (Mean Field Control) или конкурируют в командных играх со средним полем (Mean Field Team Games). В контексте управления средним полем, эти методы обеспечивают возможность определения оптимальных стратегий для каждого агента, учитывая влияние остальных агентов, представленное через среднее поле. В командных играх, они позволяют оценить равновесные стратегии для всех игроков, максимизирующие коллективную выгоду, учитывая конкуренцию и взаимодействие между агентами. Анализ в обоих случаях опирается на решение задач оптимизации, учитывающих динамику среднего поля и индивидуальные стратегии агентов.

Влияние и Перспективы Развития Методологии MF-RQE

Разработанная методология MF-RQE представляет собой мощный инструмент для анализа ситуаций, характеризующихся неполнотой информации и наличием поведенческих искажений, которые широко распространены в реальных приложениях. Данный подход позволяет учитывать и моделировать влияние когнитивных особенностей и предвзятостей, свойственных людям, на принимаемые решения, что особенно важно при прогнозировании поведения больших групп населения. В отличие от традиционных моделей, предполагающих рациональность агентов, MF-RQE позволяет создавать более реалистичные и точные прогнозы, учитывая, что люди часто действуют на основе неполной информации, эвристик и эмоциональных факторов. Это открывает новые возможности для понимания и управления сложными системами, где человеческий фактор играет ключевую роль, например, в сфере финансов, экономики и социальных наук.

Данная разработанная методология представляет собой универсальный инструмент, применимый для моделирования и прогнозирования поведения больших групп людей в различных областях знания. В экономике она способна анализировать рыночные тенденции, учитывая иррациональные факторы, влияющие на потребителей и инвесторов. В сфере финансов методология позволяет оценивать риски и оптимизировать стратегии, принимая во внимание поведенческие искажения, характерные для финансовых рынков. В социальных науках, она открывает возможности для изучения динамики общественных групп, предсказания массовых явлений и разработки эффективных политик, учитывающих психологические особенности людей. Таким образом, данный подход представляет собой ценный ресурс для исследователей и практиков, стремящихся к более глубокому пониманию сложных социальных систем и принятию обоснованных решений.

В дальнейшем планируется усовершенствование модели MF-RQE путем включения в нее более сложных механизмов взаимодействия между агентами и адаптивного обучения. Это предполагает разработку алгоритмов, позволяющих учитывать не только текущие стратегии поведения, но и способность агентов к изменениям на основе получаемого опыта и взаимодействия с другими участниками системы. Усложнение модели позволит более реалистично отражать динамику реальных процессов, в которых поведение индивидов формируется под влиянием множества факторов и постоянно адаптируется к изменяющимся условиям. Ожидается, что внедрение механизмов адаптивного обучения значительно повысит прогностическую способность MF-RQE и расширит область ее применения в различных областях науки, от экономики и финансов до социальных и биологических систем.

Исследование, представленное в данной работе, углубляется в сложность многоагентных систем, вводя концепцию MF-RQE для учета не только избегания риска, но и ограниченной рациональности. Этот подход, по сути, признает, что агенты не всегда действуют идеально, что соответствует более реалистичному взгляду на динамику принятия решений. Как однажды заметил Андрей Колмогоров: «Математика — это искусство открывать закономерности, скрытые в хаосе». В контексте данной работы, MF-RQE можно рассматривать как попытку выявить эти закономерности в хаотичном поведении большого числа агентов, предоставляя более надежный инструмент для анализа и прогнозирования равновесий в играх с участием большого числа игроков.

Что дальше?

Представленная работа, хотя и вносит вклад в понимание игр со средним полем с учетом неприятия риска и ограниченной рациональности, лишь подчеркивает глубину нерешенных вопросов. Идея равновесия MF-RQE, безусловно, интересна, но ее вычислительная сложность, особенно при увеличении размерности пространства состояний, требует дальнейшего изучения. Настоящая элегантность алгоритма проявится лишь тогда, когда удастся разработать методы его эффективной реализации, а не просто доказать его существование.

Следующим шагом видится расширение модели для учета гетерогенности агентов. Предположение об однородности начального распределения — это удобство, но не отражение реальных систем. Более того, необходимо исследовать устойчивость равновесия MF-RQE к возмущениям и шумам, неизбежно присутствующим в любой сложной системе. Оптимизация, основанная исключительно на математической чистоте, может оказаться оторванной от практической применимости.

И, пожалуй, самое важное — необходимо переосмыслить само понятие рациональности. Ограниченная рациональность — это лишь признание несовершенства агентов, но не объяснение их поведения. Поиск более адекватных моделей принятия решений, учитывающих когнитивные искажения и эвристики, — это задача, требующая не только математической строгости, но и глубокого понимания психологии и экономики. Иначе, все наши усилия сведутся к построению красивых, но бесполезных абстракций.

Оригинал статьи: https://arxiv.org/pdf/2602.13353.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-17 18:05