Квантовый скачок в оптимизации инвестиционного портфеля

Автор: Денис Аветисян

Новый алгоритм, объединяющий принципы квантовых вычислений и эволюционной оптимизации, позволяет значительно повысить эффективность управления инвестициями в условиях высокой размерности.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

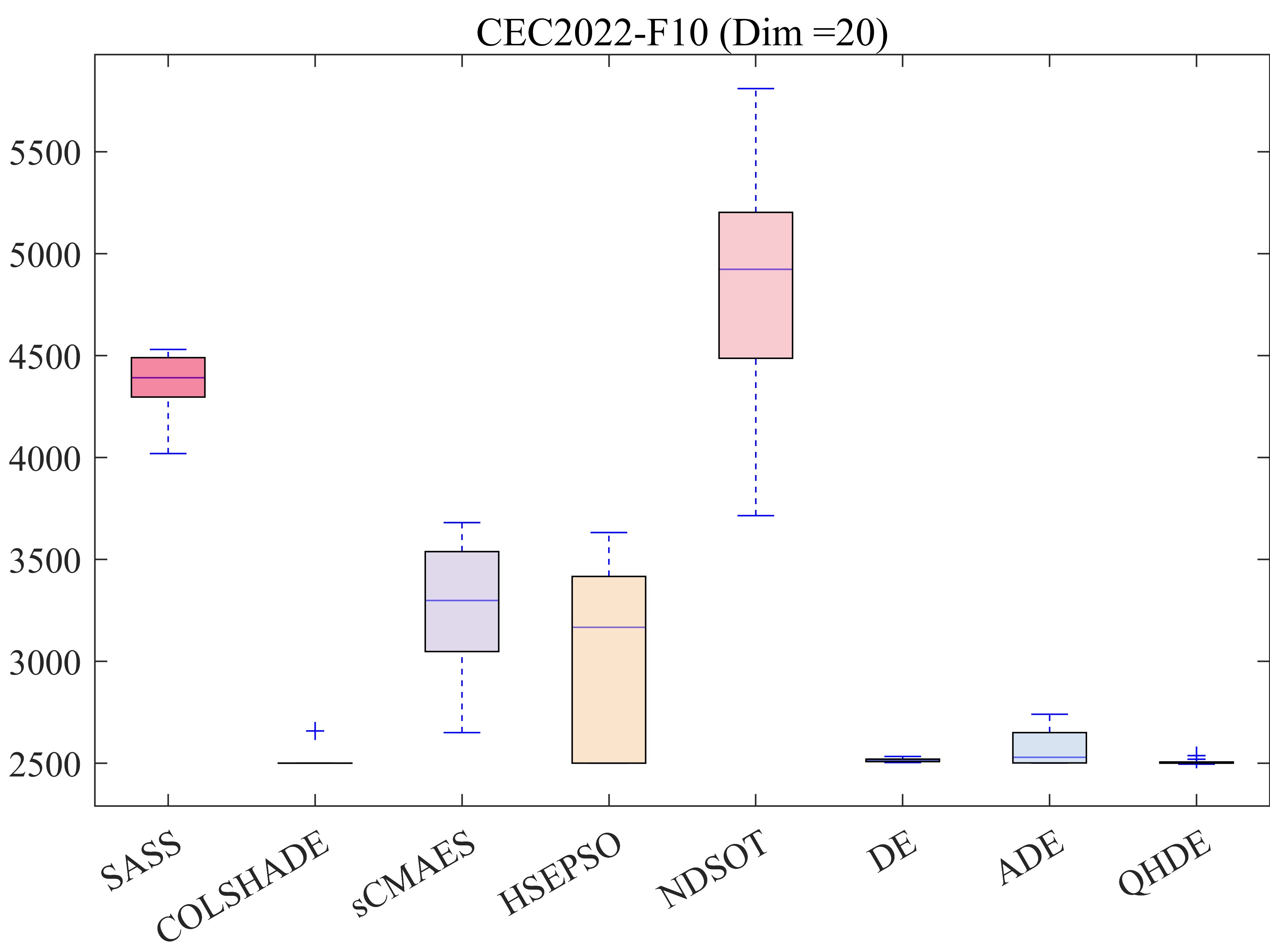
Бесплатный Телеграм канал

Оценка алгоритма QHDE на примере 20 акций демонстрирует его превосходство над другими метаэвристическими алгоритмами, подтвержденное оптимизацией целевой функции [latex]F(E)[/latex], максимизацией коэффициента Шарпа [latex]Sr[/latex] и соблюдением ограничения равенства [latex]S(E)[/latex]. — Оценка алгоритма QHDE на примере 20 акций демонстрирует его превосходство над другими метаэвристическими алгоритмами, подтвержденное оптимизацией целевой функции $F(E)$ , максимизацией коэффициента Шарпа $Sr$ и соблюдением ограничения равенства $S(E)$ .

Представлена квантово-улучшенная версия дифференциальной эволюции для решения задачи максимизации коэффициента Шарпа в портфельной оптимизации.

Оптимизация портфеля в условиях высокой размерности представляет собой сложную задачу, требующую баланса между скоростью сходимости и глобальным поиском. В данной работе, озаглавленной ‘A Quantum-Driven Evolutionary Framework for Solving High-Dimensional Sharpe Ratio Portfolio Optimization’, предложен новый квантово-вдохновленный алгоритм дифференциальной эволюции (QHDE), позволяющий значительно повысить эффективность решения этой задачи. QHDE использует принципы квантовой механики и адаптивные стратегии для улучшения поиска и повышения устойчивости алгоритма, демонстрируя превосходство над современными подходами в оптимизации портфелей, включающих от 20 до 80 активов. Может ли предложенный подход стать основой для разработки новых, более эффективных методов управления инвестициями в условиях возрастающей сложности финансовых рынков?

Разоблачение иллюзий: вызовы современной оптимизации портфеля

Традиционные методы оптимизации портфеля, такие как модель среднего значения-дисперсии $\mu - \sigma$ , зачастую оказываются неэффективными в условиях современной финансовой реальности. Данные модели, разработанные для упрощения расчетов, опираются на ряд допущений, которые не всегда соответствуют действительности. Например, предполагается нормальное распределение доходности активов и стабильность ковариационных матриц, что редко встречается на практике. Сложность современных финансовых рынков, характеризующаяся нелинейными зависимостями, высокой волатильностью и влиянием множества факторов, приводит к тому, что применение упрощенных моделей может приводить к неоптимальным инвестиционным решениям и повышенным рискам. В результате, портфели, сформированные на основе этих методов, могут оказаться недостаточно устойчивыми к изменениям рыночной конъюнктуры и не соответствовать целям инвестора.

Традиционные модели оптимизации портфеля, такие как модель среднего значения-дисперсии, зачастую опираются на упрощающие предположения, что может приводить к неоптимальным или нестабильным портфелям. Предположение о нормальном распределении доходности активов, например, не всегда соответствует действительности, особенно в периоды рыночной турбулентности или при наличии «толстых хвостов» распределения. Кроме того, упрощенное представление о корреляции между активами, игнорирующее динамику и нелинейные зависимости, может привести к недооценке рисков. В результате, портфель, оптимизированный на основе таких упрощений, может оказаться уязвимым к неожиданным рыночным изменениям и не обеспечивать желаемого уровня доходности при заданном уровне риска, или наоборот, демонстрировать чрезмерно консервативное поведение и упускать потенциальную прибыль. Поэтому, критически важно учитывать ограничения этих моделей и применять более сложные подходы, способные адекватно отражать реальные рыночные условия и характеристики активов.

Эффективное управление рисками является краеугольным камнем оптимизации инвестиционного портфеля, однако точное количественное определение и последующая минимизация этих рисков представляют собой серьезные трудности. Традиционные модели, несмотря на свою математическую элегантность, часто упрощают сложную природу финансовых рынков, не учитывая нелинейные зависимости и “черных лебедей”. Ключевая проблема заключается в том, что риск не является статичным параметром; он динамически изменяется в зависимости от множества факторов, включая макроэкономическую ситуацию, политические события и даже психологию инвесторов. Неспособность адекватно оценить и нейтрализовать эти факторы может привести к значительным потерям, даже при использовании, казалось бы, хорошо продуманной стратегии. Поэтому, разработка более сложных и адаптивных моделей управления рисками, учитывающих как систематические, так и несистематические риски, остается приоритетной задачей для финансовых аналитиков и портфельных менеджеров.

Сравнительный анализ QHDE, примененного к портфелю из 40-80 акций, показал его эффективность в сравнении с другими метаэвристическими алгоритмами.

Квантовый гибрид: новая стратегия поиска оптимальных портфелей

Квантово-гибридный дифференциальный эволюционный алгоритм (QHDE) представляет собой новый подход к задаче оптимизации портфеля, основанный на хорошо зарекомендовавшей себя эффективности алгоритма дифференциальной эволюции. В отличие от классических методов, QHDE использует принципы квантовой эволюционной стратегии для улучшения возможностей поиска и ускорения сходимости к оптимальным решениям. Данный алгоритм предназначен для эффективного определения оптимального распределения активов в портфеле с целью максимизации доходности при заданном уровне риска или минимизации риска при заданном уровне доходности. QHDE особенно эффективен в решении сложных задач оптимизации, характеризующихся высокой размерностью пространства поиска и наличием множества локальных оптимумов.

Квантический Гибридный Дифференциальный Эволюционный алгоритм (QHDE) интегрирует принципы Квантической Эволюционной Стратегии (QES) для улучшения возможностей поиска и ускорения сходимости к оптимальным решениям. В основе этого подхода лежит представление индивидуумов в виде квантовых битов (кубитов), что позволяет использовать вероятностные представления и суперпозицию состояний. Это обеспечивает более широкий охват пространства поиска по сравнению с классическими методами, такими как стандартный Дифференциальный Эволюционный алгоритм. Использование кубитов позволяет алгоритму исследовать несколько возможных решений одновременно, что способствует более быстрому обнаружению глобального оптимума и повышает эффективность оптимизации, особенно в задачах с высокой размерностью и сложной функцией потерь.

Для обеспечения устойчивой производительности, алгоритм QHDE использует динамический пул элиты (Dynamic Elite Pool), предназначенный для сохранения наиболее эффективных решений на протяжении всего процесса оптимизации. Этот пул постоянно обновляется, добавляя новые, превосходящие текущие решения, и удаляя наименее эффективные. Динамическое управление пулом элиты позволяет алгоритму QHDE избегать преждевременной сходимости к локальным оптимумам и поддерживать разнообразие популяции, что способствует более надежному поиску глобального оптимума в задачах оптимизации портфеля. Размер пула элиты является параметром алгоритма и может быть настроен для достижения оптимального баланса между скоростью сходимости и качеством решения.

Схема алгоритма QHDE иллюстрирует последовательность шагов для решения задачи оптимизации.

Усиление поиска: стратегии QHDE для расширения границ возможного

В алгоритме QHDE используется инициализация набором хороших точек (Good Point Set initialization), представляющая собой стратегическое распределение начальных решений по всему пространству поиска. Данный подход направлен на предотвращение преждевременной сходимости алгоритма к локальному оптимуму. Вместо случайного выбора начальных точек, набор хороших точек генерируется по определенным правилам, обеспечивающим равномерное покрытие пространства поиска и, следовательно, более эффективное исследование различных областей для поиска глобального оптимума. Это повышает вероятность обнаружения наилучшего решения и улучшает общую производительность алгоритма, особенно в сложных многомерных задачах оптимизации.

Алгоритм QHDE использует метод Reverse Learning на основе хаотических последовательностей для генерации разнообразной начальной популяции. Этот подход заключается в создании зеркальных решений относительно известных экстремальных точек, что позволяет исследовать пространство поиска более эффективно. Хаотические последовательности, благодаря своей непредсказуемости и чувствительности к начальным условиям, обеспечивают широкое покрытие пространства решений, снижая вероятность преждевременной сходимости алгоритма к локальному оптимуму и расширяя область поиска глобального оптимума. Генерация начальной популяции с использованием Reverse Learning способствует более полному и разнообразному исследованию пространства решений на начальных этапах оптимизации.

Для введения контролируемой случайности, алгоритм QHDE использует возмущение на основе распределения Коши-Гаусса. Данный метод предполагает добавление случайных величин, сгенерированных на основе комбинации распределения Коши и нормального (Гаусса) распределения, к текущим решениям. Использование распределения Коши обеспечивает более широкие, но менее частые, скачки в пространстве поиска, в то время как нормальное распределение обеспечивает более мелкие и частые корректировки. Комбинация этих двух распределений позволяет QHDE эффективно исследовать пространство решений, избегая преждевременной сходимости к локальным оптимумам и поддерживая адаптивность алгоритма в сложных поисковых ландшафтах. Величины возмущений регулируются для баланса между интенсивностью исследования и точностью эксплуатации.

Результаты экспериментов на тестовом наборе CEC 2022 демонстрируют превосходство алгоритма QHDE по сравнению с другими методами оптимизации.

Оптимизированные портфели и доходность с учетом риска: взгляд в будущее

Алгоритм QHDE демонстрирует значительное улучшение показателей инвестиционного портфеля за счет выявления решений, лежащих на так называемой эффективной границе. Эта граница представляет собой множество портфелей, предлагающих максимальную ожидаемую доходность при заданном уровне риска, или минимальный риск при заданной доходности. QHDE, путем оптимизации, позволяет инвесторам находить оптимальные комбинации активов, избегая неэффективных портфелей, которые не обеспечивают наилучшего соотношения между риском и доходностью. Данный подход позволяет максимизировать прибыль при приемлемом уровне риска, что особенно важно в условиях высокой волатильности рынка, и обеспечивает превосходство над традиционными методами формирования портфеля, не учитывающими принципы эффективной границы.

Алгоритм QHDE демонстрирует значительное улучшение показателей инвестиционных портфелей за счет максимизации доходности при заданном уровне риска. Этот подход непосредственно влияет на коэффициент Шарпа $(S = (R_p - R_f) / \sigma_p)$ , который является ключевым инструментом оценки эффективности инвестиционных стратегий. Повышение коэффициента Шарпа указывает на то, что инвестор получает более высокую доходность за единицу принятого риска. QHDE, оптимизируя соотношение между прибылью и риском, позволяет формировать портфели, которые превосходят традиционные подходы и обеспечивают более привлекательные результаты для инвесторов, стремящихся к увеличению прибыли при сохранении приемлемого уровня риска.

Исследование продемонстрировало превосходство алгоритма QHDE над семью передовыми алгоритмами оптимизации портфеля. В частности, применительно к портфелю из 60 акций, QHDE достиг улучшения целевой функции до 73,4%, достигнув значения 26,66. Данный алгоритм последовательно демонстрирует более высокую доходность с учетом риска, подтверждаясь стабильно самым высоким коэффициентом Шарпа $\frac{R_p - R_f}{\sigma_p}$ во всех рассмотренных размерах портфеля. Эти результаты указывают на значительный потенциал QHDE для повышения эффективности инвестиционных стратегий и достижения оптимального соотношения между прибылью и риском.

Алгоритм демонстрирует исключительную точность в соблюдении заданных ограничений, что подтверждается стабильным приближением значения Equality Constraint к единице в процессе оптимизации. Такая высокая степень соответствия условиям, установленным для формирования портфеля, является ключевым фактором, обеспечивающим надежность и предсказуемость результатов. В отличие от многих других алгоритмов, которые могут допускать отклонения от заданных параметров, данный алгоритм гарантирует, что все ограничения выполняются практически идеально, что позволяет инвесторам быть уверенными в соответствии портфеля их требованиям и целям. Это особенно важно в сложных финансовых моделях, где даже небольшие отклонения могут привести к значительным потерям или нежелательным рискам.

Исследование демонстрирует стремление к преодолению границ существующих методов оптимизации портфеля. Авторы предлагают не просто улучшение, а принципиально иной подход, основанный на квантовых принципах и адаптивной стратегии дифференциальной эволюции. Этот поиск эффективности напоминает слова Кena Thompson: “Программы должны быть достаточно маленькими, чтобы их можно было понять.” Именно стремление к ясности и пониманию лежало в основе создания QHDE, алгоритма, способного эффективно решать задачи высокой размерности, превосходя существующие решения в поиске оптимального соотношения риска и доходности, то есть максимизации коэффициента Шарпа. Подобно тому, как Thompson стремился к лаконичности кода, данная работа демонстрирует элегантность в достижении сложной цели — глобальной оптимизации.

Куда Дальше?

Представленная работа, по сути, демонстрирует не просто оптимизацию портфеля, а локальный взлом системы поиска решений в многомерном пространстве. Эффективность предложенного алгоритма QHDE — это не столько торжество квантовых вычислений, сколько свидетельство того, что даже незначительное нарушение стандартных процедур дифференциальной эволюции способно открыть неожиданные пути к глобальному оптимуму. Однако, взлом всегда порождает вопросы. Устойчивость алгоритма к различным типам шума и нелинейностям, его масштабируемость при увеличении размерности портфеля — всё это требует дальнейшей, бескомпромиссной проверки.

Очевидно, что истинный потенциал QHDE раскроется не в гонке за максимальной Sharpe Ratio, а в адаптации его принципов к другим задачам глобальной оптимизации. Можно ли экстраполировать эту квантово-вдохновленную стратегию на задачи машинного обучения, комбинаторной химии или даже моделирование сложных социальных систем? Вероятно, да. Но для этого потребуется отбросить иллюзию, что квантовые вычисления — это панацея, и сосредоточиться на поиске тех узких мест в существующих алгоритмах, где даже небольшая “квантовая” модификация может дать значительный эффект.

В конечном счете, важно помнить: оптимизация — это лишь временное решение. Реальный мир редко предоставляет идеально гладкие поверхности для поиска минимумов и максимумов. Будущие исследования должны быть направлены на создание алгоритмов, способных адаптироваться к непредсказуемости и неопределенности, алгоритмов, которые не просто находят решение, но и понимают его ограничения.

Оригинал статьи: https://arxiv.org/pdf/2601.11029.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-19 06:53