Обучение с Учётом Риска в Неустойчивых Условиях

Автор: Денис Аветисян

Новый подход позволяет алгоритмам адаптироваться к меняющимся функциям и уровням риска, обеспечивая надежное обучение в динамичных средах.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Алгоритмы ценообразования, игнорирующие изменчивость рисков и функциональности, демонстрируют снижение эффективности по сравнению с оптимальными стратегиями - как статическими, так и динамическими, полученными методом полного перебора - что подтверждается увеличением значений CVaR и, как следствие, ростом динамического сожаления. — Алгоритмы ценообразования, игнорирующие изменчивость рисков и функциональности, демонстрируют снижение эффективности по сравнению с оптимальными стратегиями — как статическими, так и динамическими, полученными методом полного перебора — что подтверждается увеличением значений CVaR и, как следствие, ростом динамического сожаления.

Исследование разработало и проанализировало алгоритмы оптимизации первого и нулевого порядка для обучения с учётом риска в нестационарных условиях, предоставляя границы динамического сожаления, адаптирующиеся к изменениям функций и уровней риска.

В задачах оптимизации, связанных с принятием решений в условиях неопределенности, статичные модели часто не учитывают динамически меняющийся уровень риска. Настоящая работа, ‘Risk-Averse Learning with Varying Risk Levels’, посвящена разработке алгоритмов онлайн-оптимизации, адаптирующихся к изменяющимся уровням риска и использующих CVaR в качестве меры риска. Предложенные алгоритмы первого и нулевого порядка демонстрируют ограниченные динамические границы сожаления, зависящие от вариации функции и уровня риска. Способны ли эти подходы обеспечить надежное принятие решений в сложных, нестационарных средах, требующих учета риска?

Временные Изменения и Риск: Основы Обучения в Неопределенности

Традиционные алгоритмы онлайн-обучения зачастую сосредотачиваются на минимизации средней стоимости, игнорируя при этом так называемый «хвостовой риск» и возможность значительных потерь. Такой подход, хотя и эффективен в стабильных условиях, может оказаться катастрофическим в динамичных средах, где распределение затрат подвержено изменениям. В то время как средняя стоимость дает представление об общей производительности, она не учитывает экстремальные, но вполне вероятные сценарии, которые могут привести к существенным убыткам. В результате, система, оптимизированная исключительно для средней стоимости, может оказаться крайне уязвимой к неожиданным событиям и подвергнуться серьезным негативным последствиям, даже если в большинстве случаев она демонстрирует удовлетворительные результаты. Данная особенность особенно критична в областях, где цена ошибки высока, например, в финансах или в системах управления рисками.

В условиях постоянно меняющейся среды, где распределения затрат со временем претерпевают изменения, стратегия, основанная исключительно на минимизации средней стоимости, может приводить к неприемлемым последствиям. Традиционные алгоритмы, стремящиеся к оптимизации среднего значения, не учитывают так называемый «хвост» распределения — вероятность редких, но значительных потерь. Представьте себе систему, оптимизированную для снижения средней задержки в сети; она может прекрасно работать в обычных условиях, но оказаться неспособной справиться с внезапным всплеском трафика или сбоем оборудования, приводящим к катастрофическим задержкам. Таким образом, фокусировка только на среднем значении игнорирует важные риски и может привести к серьезным убыткам в динамичных и непредсказуемых системах, где необходимо учитывать не только наиболее вероятные, но и наихудшие сценарии развития событий.

Условная ценность под риском (Conditional Value-at-Risk, CVaR) представляет собой последовательный и выпуклый подход к управлению так называемым «хвостовым риском» — вероятностью экстремальных потерь, которые могут возникнуть в динамичных средах. В отличие от методов, ориентированных исключительно на минимизацию средней стоимости, CVaR концентрируется на анализе наихудших сценариев, оценивая среднюю потерю, возникающую в α% самых неблагоприятных ситуациях. Этот подход позволяет более эффективно учитывать потенциальные катастрофические последствия, обеспечивая более надежную стратегию обучения в условиях неопределенности и изменчивости, поскольку позволяет оптимизировать алгоритмы, направленные на минимизацию риска именно в критических ситуациях, а не просто усреднять общие показатели.

Разработка алгоритмов, способных эффективно оценивать и оптимизировать условное значение в худшем случае (Conditional Value-at-Risk — CVaR) в условиях онлайн-обучения, представляет собой ключевую задачу современной исследовательской повестки. В динамически меняющихся средах, где распределения затрат претерпевают изменения во времени, традиционные методы оптимизации, ориентированные на минимизацию средней стоимости, оказываются недостаточными для обеспечения надежности и устойчивости к неблагоприятным сценариям. Новые алгоритмы стремятся не только предсказывать средние значения, но и учитывать «хвост» распределения, фокусируясь на минимизации потенциальных убытков в наихудших ситуациях. Эффективная оценка CVaR требует разработки методов, способных быстро адаптироваться к изменяющимся данным и обеспечивать точную оценку риска в режиме реального времени, что открывает возможности для создания более надежных и устойчивых систем обучения с подкреплением и других алгоритмов машинного обучения.

Анализ CVaR и динамического сожаления показывает, что разработанные алгоритмы (первого и нулевого порядка) демонстрируют сопоставимые результаты с оптимальным ценообразованием при заданном уровне риска и целевой заполняемости.

Онлайн-Обучение с CVaR: Алгоритмы и Методы Оптимизации

Алгоритм онлайн-обучения является базовым компонентом, последовательно обновляющим прогнозы на основе поступающих данных. В отличие от традиционных алгоритмов пакетной обработки, онлайн-обучение обрабатывает данные по мере их поступления, что позволяет модели адаптироваться к изменениям в распределении данных в реальном времени. Каждый поступающий пример используется для немедленного обновления параметров модели, что требует меньших вычислительных ресурсов и памяти по сравнению с переобучением модели на всем наборе данных. Процесс обновления обычно включает в себя вычисление функции потерь на основе текущего примера и использование этой информации для корректировки параметров модели с помощью, например, градиентного спуска. Таким образом, алгоритм онлайн-обучения позволяет создавать адаптивные и эффективные модели для задач, где данные поступают потоком.

Для оптимизации CVaR (Conditional Value-at-Risk) рассматриваются два основных подхода: методы первого порядка и методы нулевого порядка. Методы первого порядка, такие как градиентный спуск, используют информацию о градиенте функции потерь для эффективной оптимизации, что требует вычисления производных. Методы нулевого порядка, напротив, применяются в случаях, когда градиент недоступен или его вычисление затруднено. Они полагаются исключительно на вычисление значений функции и используют методы стохастической аппроксимации для приближения к оптимальному решению. Выбор метода определяется доступностью градиентной информации и вычислительными ресурсами, при этом методы первого порядка обычно обеспечивают более быструю сходимость, но требуют дополнительных вычислений.

Первичные методы оптимизации, использующие информацию о градиенте, обеспечивают эффективную оптимизацию при решении задач CVaR в онлайн-обучении. В их основе лежит использование $\nablaf(x)$ , вектора градиента функции потерь $f(x)$ в текущей точке $x$ . Одним из наиболее распространенных методов является градиентный спуск (Gradient Descent), который итеративно обновляет параметры модели в направлении, противоположном градиенту, с целью минимизации функции потерь. Скорость обучения (learning rate) является ключевым гиперпараметром, определяющим размер шага на каждой итерации. Для повышения эффективности и ускорения сходимости применяются различные модификации градиентного спуска, такие как стохастический градиентный спуск (Stochastic Gradient Descent) и методы с использованием момента (momentum-based methods).

Методы нулевого порядка (Zeroth-Order Methods) применяются в задачах оптимизации, когда вычисление градиента целевой функции невозможно или нецелесообразно. Вместо этого, они полагаются исключительно на оценки самой функции. Для реализации оптимизации в данном случае используются методы стохастической аппроксимации, которые строят последовательность оценок оптимального решения на основе случайных выборок данных. Ключевым элементом является итеративное обновление параметров модели, основанное на разнице между текущей оценкой функции и предыдущими оценками, позволяющее приблизиться к оптимальному значению функции без использования информации о ее производных. Эффективность таких методов зависит от выбора шага обучения и скорости сходимости алгоритма стохастической аппроксимации.

Алгоритмы обучения первого и нулевого порядка генерируют цены парковки, стремящиеся к целевой заполняемости (38) при заданном уровне риска (40), что приводит к соответствующим траекториям заполняемости, сравнимым с оптимальными ценами [latex]x_{t}^{\ast}[/latex]. — Алгоритмы обучения первого и нулевого порядка генерируют цены парковки, стремящиеся к целевой заполняемости (38) при заданном уровне риска (40), что приводит к соответствующим траекториям заполняемости, сравнимым с оптимальными ценами $x_{t}^{\ast}$ .

Адаптация к Изменениям: Динамические Среды и Производительность Алгоритмов

В реальных условиях функционирования алгоритмов, наблюдается вариация функции потерь (Function Variation), заключающаяся в изменении распределения затрат во времени. Это представляет собой серьезную проблему для онлайн-алгоритмов, поскольку предположения о стационарности функции потерь нарушаются. Изменение распределения затрат требует от алгоритма постоянной адаптации к новым условиям, что усложняет процесс оптимизации и может приводить к снижению эффективности. В частности, алгоритмы, основанные на предположении о неизменности функции, могут давать неоптимальные решения при наличии значительной Function Variation. Количественная оценка степени вариации функции потерь, обозначенная как $V_f$ , является важным параметром при анализе производительности алгоритмов в динамических средах.

Изменение уровня допустимого риска, или вариация уровня риска (Risk-Level Variation), существенно усложняет процесс оптимизации в онлайн-алгоритмах. Это связано с тем, что предпочтения пользователя относительно компромисса между ожидаемыми затратами и уровнем риска могут меняться со временем. Алгоритмы, разработанные для статического уровня риска, могут оказаться неэффективными или даже неоптимальными при динамически меняющихся предпочтениях. Необходимость адаптации к меняющемуся отношению к риску требует от алгоритмов постоянной оценки и корректировки стратегии принятия решений, что добавляет вычислительную сложность и может привести к увеличению regret.

Для точной оценки градиентов CVaR в динамических средах алгоритмы используют приближение истинного распределения затрат посредством эмпирического распределения затрат. Этот подход заключается в построении оценки распределения на основе наблюдаемых исторических данных о затратах. Эмпирическое распределение, формируемое на основе выборки из $n$ наблюдений, позволяет оценить вероятность различных уровней затрат и, следовательно, вычислить градиент CVaR. Применение эмпирического распределения является ключевым элементом в онлайн-алгоритмах, поскольку истинное распределение затрат обычно неизвестно и необходимо оценивать на протяжении времени, адаптируясь к изменяющимся условиям среды.

Точность аппроксимации истинного распределения затрат, используемой для оценки градиентов CVaR в динамических средах, ограничена статистическими инструментами, в частности, неравенством DKW (Dudley-Kolmogorov-Wasserman). Неравенство DKW предоставляет верхнюю границу на разницу между эмпирическим распределением и истинным распределением, обеспечивая надежные оценки градиентов даже при ограниченном объеме данных. Это позволяет алгоритмам сохранять работоспособность в условиях Function Variation и Risk-Level Variation, гарантируя, что оценки градиентов остаются достаточно точными для эффективной оптимизации. Формально, неравенство DKW позволяет оценить ошибку аппроксимации с заданной вероятностью, что критически важно для получения теоретических гарантий сходимости и производительности алгоритма.

Анализ показывает, что для методов первого и нулевого порядка существуют динамические границы сожаления. Для метода первого порядка эта граница выражается как $O(T^(1-a/4)V_f^(1/5))$ , а для метода нулевого порядка — как $O(T^(4/5)V_α^(1/5))$ . В этих выражениях $T$ обозначает горизонт времени, $V_f$ — величину вариации функции потерь, а $V_α$ — величину вариации уровня риска. Эти границы характеризуют производительность алгоритмов в динамических средах, учитывая как временной фактор, так и степень изменения функции и уровня риска, что позволяет оценить их эффективность в условиях нестабильности.

Алгоритм 1 генерирует цены, сопоставимые с оптимальными по критерию наименьшего риска [latex]x_{t}^{\ast}[/latex], при различных уровнях риска [latex]V_{\alpha}^{1}[/latex], [latex]V_{\alpha}^{2}[/latex] и [latex]V_{\alpha}^{3}[/latex], что демонстрирует низкое динамическое сожаление. — Алгоритм 1 генерирует цены, сопоставимые с оптимальными по методу полного перебора $x_t^*$ , демонстрируя близкие значения CVaR и динамическое сожаление при различных стратегиях $n_t = \{1, 4, 16\}$ .

Практическое Применение и Перспективы Развития

Количество необходимых выборок для достижения заданной точности, известное как выборочная сложность алгоритмов, играет определяющую роль в их практическом применении. Эффективность алгоритма напрямую зависит от его способности быстро обучаться на ограниченном объеме данных, особенно в ситуациях, когда сбор данных требует значительных затрат или времени. Алгоритмы, демонстрирующие низкую выборочную сложность, позволяют снизить вычислительные ресурсы и время обучения, что критически важно для работы в динамичных средах, где условия постоянно меняются. В контексте онлайн-обучения, где данные поступают последовательно, минимизация необходимого количества выборок становится еще более важной, поскольку позволяет алгоритму оперативно адаптироваться к новым условиям и поддерживать высокую производительность на протяжении всего периода эксплуатации. Таким образом, анализ и оптимизация выборочной сложности являются ключевыми задачами для повышения практической ценности и конкурентоспособности онлайн-алгоритмов.

Алгоритмы, способные минимизировать сложность выборки — то есть количество необходимых данных для достижения заданной точности — при сохранении устойчивости к изменениям в окружающей среде, представляют собой значительное преимущество в практических приложениях. Эффективное использование данных особенно важно в ситуациях, где сбор информации затруднен или требует больших затрат, например, при работе с потоковыми данными или в условиях ограниченных ресурсов. Способность быстро адаптироваться к динамическим изменениям позволяет таким алгоритмам поддерживать высокую производительность даже в нестабильных средах, что делает их незаменимыми в широком спектре задач, от финансовых прогнозов до управления роботизированными системами и оптимизации логистических процессов. Разработка подобных алгоритмов является ключевым направлением современных исследований в области машинного обучения и искусственного интеллекта.

Представленная работа предлагает структурированный подход к анализу и сопоставлению различных алгоритмов онлайн-обучения, используя понятие динамического сожаления — метрику, отражающую суммарные потери по сравнению с наилучшим фиксированным решением. Данный подход позволяет оценить эффективность алгоритмов в изменяющихся условиях, где оптимальное решение со временем может меняться. Оценивая динамическое сожаление, можно сравнивать, насколько быстро алгоритм адаптируется к новым данным и минимизирует общие потери по сравнению с постоянной стратегией, что особенно важно для приложений, требующих непрерывного обучения и принятия решений в реальном времени. Полученные результаты способствуют более глубокому пониманию компромиссов между скоростью обучения, точностью и устойчивостью различных алгоритмов в динамических средах, что открывает возможности для разработки более эффективных и надежных систем машинного обучения.

Результаты, представленные на Рисунке 6, наглядно демонстрируют значительное снижение как условной ценности под риском (CVaR), так и динамического сожаления при увеличении объема выборки с 1 до 16. Данная закономерность подчеркивает критическую важность эффективности использования данных в алгоритмах онлайн-обучения. Более крупная выборка позволяет алгоритму точнее оценивать функцию потерь и адаптироваться к изменениям в динамической среде, что, в свою очередь, приводит к уменьшению накопленных потерь и, следовательно, к снижению динамического сожаления. Это указывает на то, что для достижения оптимальной производительности в реальных условиях крайне важно стремиться к максимальной информативности каждой используемой выборки и эффективно использовать доступные данные.

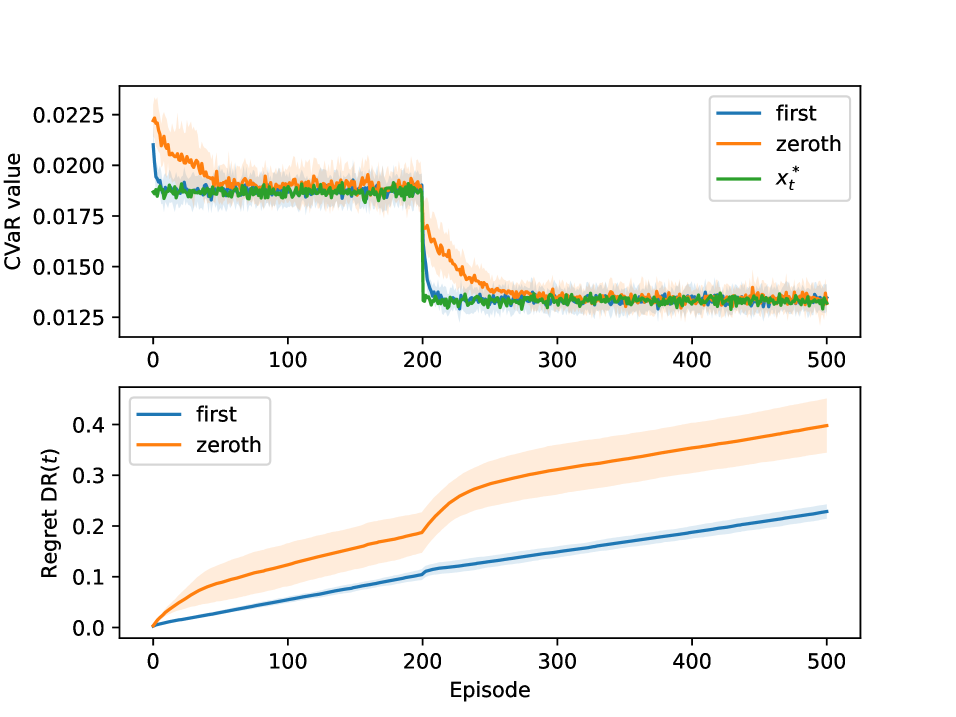
Результаты моделирования продемонстрировали более высокую скорость сходимости алгоритма первого порядка по сравнению с алгоритмом нулевого порядка. Анализ показателей CVaR (Conditional Value at Risk) и динамического сожаления, представленный на рисунках 1 и 2, наглядно подтверждает данное утверждение. Более низкие значения CVaR свидетельствуют о меньшем риске значительных потерь, а снижение динамического сожаления указывает на то, что алгоритм быстрее приближается к оптимальному решению в динамически изменяющейся среде. Таким образом, алгоритм первого порядка представляется более эффективным инструментом для задач онлайн-обучения, требующих быстрой адаптации и минимизации рисков.

Перспективные исследования должны быть направлены на создание адаптивных алгоритмов, способных автоматически подстраиваться под изменяющиеся уровни вариации функции и риска. Такая адаптивность критически важна для повышения практической применимости алгоритмов в реальных условиях, где стационарность данных — скорее исключение, чем правило. Разработка алгоритмов, способных оценивать степень изменчивости окружающей среды и соответствующим образом корректировать стратегию обучения, позволит значительно улучшить их производительность и надежность в динамически меняющихся сценариях. Особое внимание следует уделить разработке методов, позволяющих алгоритмам эффективно использовать доступные данные для оценки этих изменений и оперативной адаптации к ним, что позволит минимизировать кумулятивные потери и обеспечит устойчивость к неожиданным колебаниям.

Алгоритм 1 генерирует цены, сопоставимые с оптимальными по методу полного перебора [latex]x_t^*[/latex], демонстрируя близкие значения CVaR и динамическое сожаление при различных стратегиях [latex]n_t = \{1, 4, 16\}[/latex]. — Алгоритм 1 генерирует цены, сопоставимые с оптимальными по методу полного перебора $x_t^*$ , демонстрируя близкие значения CVaR и динамическое сожаление при различных стратегиях $n_t = \{1, 4, 16\}$ .

Исследование, представленное в данной работе, демонстрирует стремление к созданию систем, способных адаптироваться к изменяющимся условиям и уровням риска. Этот подход перекликается с мыслями Макса Планка: «В науке всегда есть то, чего мы не знаем». Действительно, алгоритмы, разработанные для онлайн-обучения в нестационарных средах, учитывают не только функцию, но и вариации уровня риска, стремясь к минимизации динамического сожаления. Подобно тому, как физик принимает неопределенность, данное исследование признает изменчивость окружающей среды и разрабатывает решения, способные сохранять устойчивость даже в условиях постоянных изменений. Акцент на адаптивности и долговечности алгоритмов отражает понимание того, что любая абстракция несет груз прошлого, и только медленные изменения обеспечивают стабильность системы.

Куда же дальше?

Представленная работа, подобно любому алгоритму, лишь временно отсрочила неизбежное — наступление новых, более сложных условий. Достигнутые границы динамического сожаления, хоть и адаптируются к изменчивости функций и уровней риска, всё же подразумевают статичность самой структуры неблагоприятной среды. Будущие исследования, вероятно, столкнутся с необходимостью разработки методов, способных учиться не только в меняющемся ландшафте, но и в условиях эволюционирующей самой концепции риска. Версионирование алгоритмов — это форма памяти, но даже самая совершенная память не может предвидеть все возможные мутации среды.

Особое внимание, несомненно, потребуется уделить взаимодействию между алгоритмами, стремящимися к минимизации риска, и системами, намеренно создающими неопределенность. Стрела времени всегда указывает на необходимость рефакторинга, однако в динамических средах рефакторинг должен быть не реакцией на изменения, а предвидением их. Игнорирование асимметрии между активным и пассивным обучением — упущенная возможность.

Наконец, следует признать, что стремление к абсолютной безопасности — иллюзия. Оптимизация в условиях неопределенности — это не поиск идеального решения, а поиск наиболее достойного способа старения. В конечном счете, ценность алгоритма определяется не его способностью избежать ошибок, а его способностью извлекать уроки из неизбежных потерь.

Оригинал статьи: https://arxiv.org/pdf/2512.22986.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-12-31 08:35