Онлайн-обучение с ограничениями: Новый алгоритм CLASP

Автор: Денис Аветисян

В статье представлен алгоритм CLASP, позволяющий эффективно решать задачи онлайн-обучения с динамически изменяющимися ограничениями.

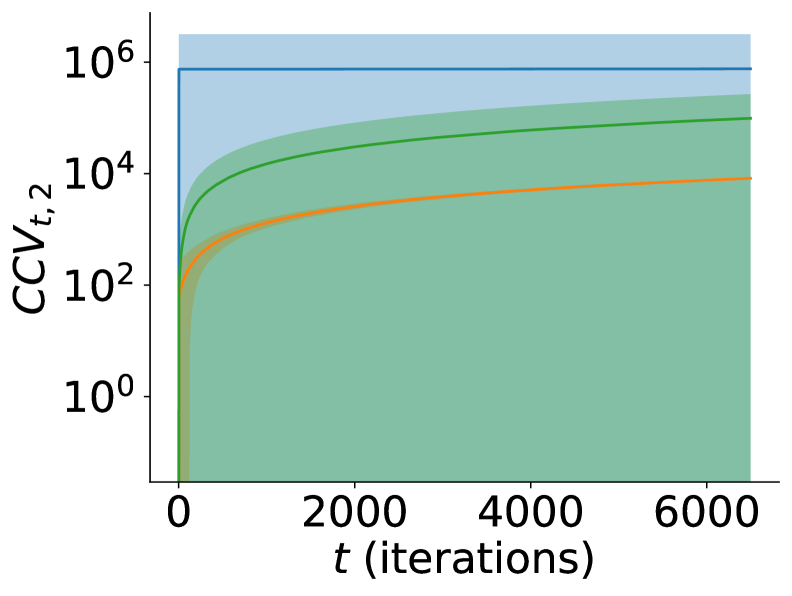
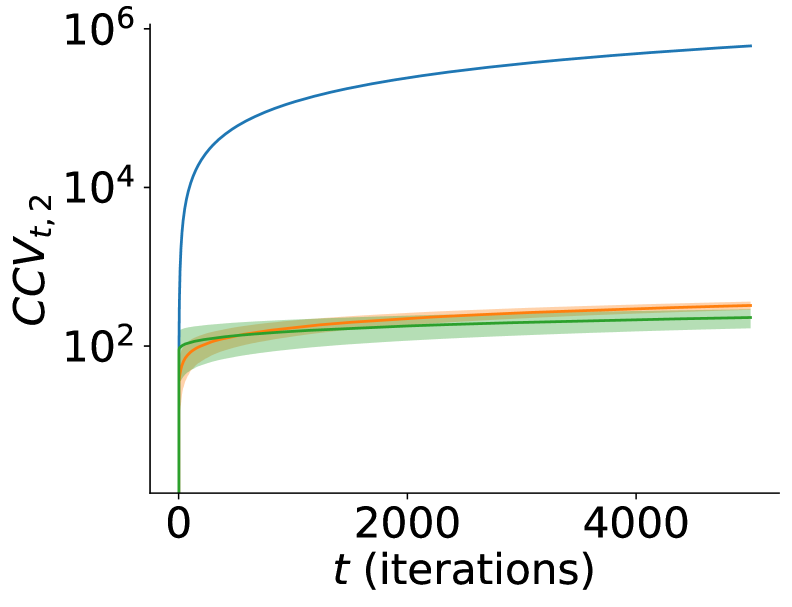
В исследовании онлайн-регрессии с антагонистическими ограничениями алгоритм AdaGrad демонстрирует минимальные потери, но за счет значительных нарушений ограничений, в то время как CLASP обеспечивает сопоставимый контроль над обоими показателями нарушений с RECOO, при этом требуя меньше памяти, а Switch достигает наименьших нарушений, но с более высокой вычислительной сложностью на каждой итерации; все значения [latex]\mathrm{CCV}_{T,2}[/latex] представлены после проведения анализа. — В исследовании онлайн-регрессии с антагонистическими ограничениями алгоритм AdaGrad демонстрирует минимальные потери, но за счет значительных нарушений ограничений, в то время как CLASP обеспечивает сопоставимый контроль над обоими показателями нарушений с RECOO, при этом требуя меньше памяти, а Switch достигает наименьших нарушений, но с более высокой вычислительной сложностью на каждой итерации; все значения $\mathrm{CCV}_{T,2}$ представлены после проведения анализа.

Алгоритм CLASP обеспечивает логарифмические оценки как сожаления, так и кумулятивного нарушения ограничений в задачах онлайн-выпуклой оптимизации.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

В условиях динамически меняющихся ограничений, задача онлайн оптимизации с выпуклыми функциями потерь часто сталкивается с компромиссом между минимизацией потерь и соблюдением ограничений. В данной работе представлена новая стратегия, ‘CLASP: An online learning algorithm for Convex Losses And Squared Penalties’, предназначенная для решения задач онлайн оптимизации с выпуклыми функциями потерь и квадратичными штрафами за нарушение ограничений. Алгоритм CLASP обеспечивает гарантированную сходимость к логарифмическим границам как для кумулятивных потерь (регрета), так и для кумулятивных квадратичных штрафов, что является новым результатом для данной области. Какие перспективы открывает применение CLASP для решения задач машинного обучения с динамическими ограничениями в реальном времени?

Основы последовательных решений в условиях ограничений

Многие задачи, с которыми сталкивается современная наука и техника, требуют принятия последовательных решений в условиях ограничений. Например, управление роботом, планирование логистических маршрутов или оптимизация финансовых портфелей — во всех этих случаях необходимо учитывать различные факторы, такие как физические ограничения, временные рамки, бюджетные ограничения и прочие. Эффективное решение подобных задач требует не просто поиска оптимального решения в каждый момент времени, но и обеспечения его устойчивости к неопределенностям и изменениям внешней среды. Поэтому, для успешного функционирования в реальных условиях, необходимы надежные и гибкие алгоритмы оптимизации, способные учитывать эти ограничения и обеспечивать робастность принимаемых решений. Разработка таких алгоритмов является ключевой задачей в области искусственного интеллекта и оптимизационных методов.

Онлайн-оптимизация выпуклых функций (OCO) представляет собой эффективный подход к решению задач, где решения принимаются последовательно, а цель — минимизировать функцию потерь. Однако, стандартные алгоритмы OCO часто сталкиваются с трудностями при работе с ограничениями, которые часто встречаются в реальных приложениях. Эти ограничения могут касаться ресурсов, безопасности или других важных факторов, и их игнорирование может привести к нереалистичным или нежелательным решениям. В результате, прямая реализация ограничений в рамках стандартной схемы OCO требует сложных преобразований или штрафных функций, что может снизить эффективность и точность оптимизации. Поэтому, для решения задач, где ограничения играют ключевую роль, необходимы более специализированные подходы, способные напрямую учитывать эти факторы в процессе принятия решений.

Ограниченная онлайн-оптимизация выпуклых функций (COCO) представляет собой расширение стандартной онлайн-оптимизации выпуклых функций, направленное на решение задач, где каждое решение должно удовлетворять определенным ограничениям. В отличие от OCO, которая предполагает неограниченную оптимизацию, COCO вводит механизмы для обеспечения соблюдения этих ограничений на каждом шаге принятия решения. Это достигается за счет включения в процесс оптимизации штрафных функций или проекций, которые корректируют решения, нарушающие заданные границы. Таким образом, COCO позволяет эффективно решать широкий спектр практических задач, где важно не только минимизировать функцию потерь, но и соблюдать определенные правила и условия, например, в задачах управления ресурсами, робототехнике и финансовом моделировании. $\min_{x \in X} f(x) \text{ subject to } g(x) \leq 0$ .

Онлайн-метод опорных векторов позволяет классифицировать данные последовательно, по мере их поступления.

Оценка эффективности: Сожаление и нарушение ограничений

В контексте онлайн-обучения, метрика “Регрет” (Regret) количественно определяет разницу между производительностью обучающего алгоритма и производительностью наилучшего фиксированного действия, выбранного заранее, если оценивать в ретроспективе. Формально, $Регрет = E[Оптимальное фиксированное действие] - E[Алгоритм обучения]$ , где E обозначает математическое ожидание. Высокое значение регрета указывает на то, что алгоритм обучения мог бы достичь значительно лучших результатов, если бы изначально выбрал другое, постоянное действие. Данная метрика позволяет оценить эффективность алгоритма в сравнении с простым, но заранее определенным подходом.

Помимо метрики сожаления (Regret), для практического применения алгоритмов обучения с подкреплением критически важно минимизировать кумулятивное нарушение ограничений (Cumulative Constraint Violation, CCV). CCV позволяет оценивать степень нарушения заданных ограничений в процессе обучения, обеспечивая возможность построения решений, реализуемых в реальных условиях. Использование CCV необходимо для предотвращения ситуаций, когда алгоритм, демонстрирующий минимальное сожаление, предлагает невыполнимые или нежелательные действия с точки зрения практической реализации. Выделяют два варианта расчета CCV: CCV1, суммирующий абсолютные значения нарушений, и CCV2, использующий квадратичные отклонения, что позволяет сильнее штрафовать значительные нарушения ограничений.

Кумулятивное нарушение ограничений (CCV) оценивается двумя способами: CCV1, суммирующим абсолютные значения нарушений, и CCV2, вычисляемым как сумма квадратов нарушений. В отличие от CCV1, который линейно реагирует на каждое нарушение, CCV2 применяет квадратичную функцию штрафа. Это означает, что значительные нарушения ограничений оказывают непропорционально большее влияние на общую оценку CCV2, обеспечивая более сильную пенализацию за серьезные отступления от заданных условий и способствуя более надежному соблюдению ограничений в процессе обучения. $CCV2 = \sum_{t=1}^{T} (v_t)^2$ , где $v_t$ — величина нарушения ограничения в момент времени t.

Онлайн-регрессия с дополнительными итерациями позволяет улучшить точность модели в процессе обучения.

CLASP: Новый алгоритм для COCO

Алгоритм CLASP — это новая методика, разработанная специально для решения задач онлайн выпуклой оптимизации с ограничениями (Constrained Online Convex Optimization, COCO). В отличие от существующих подходов, CLASP ориентирован на динамическую адаптацию к ограничениям в процессе обучения, что позволяет эффективно управлять компромиссом между минимизацией потерь и соблюдением заданных ограничений. Данный алгоритм предназначен для обработки потоковых данных, где необходимо принимать решения на основе последовательно поступающей информации, при этом гарантируя выполнение определенных ограничений на протяжении всего процесса обучения. Особенностью CLASP является его способность к работе в условиях, когда функция потерь и ограничения могут изменяться со временем, что делает его применимым в широком спектре задач, включая машинное обучение с ограничениями и управление ресурсами.

Алгоритм CLASP использует свойство ‘Firm Non-Expansiveness’ (строгая нерасширяемость) в своем операторе проекции, что существенно упрощает анализ сходимости. Данное свойство гарантирует, что проекция не увеличивает расстояние между точками, что позволяет доказать ограниченность изменений при итерациях алгоритма. Математически, Firm Non-Expansiveness означает, что для любых векторов $x$ и $y$ , $||P(x) - P(y)|| \leq ||x - y||$ , где $P$ — оператор проекции. Использование Firm Non-Expansiveness позволяет получить более четкие и строгие оценки скорости сходимости и обеспечить гарантии по ограничению нарушения ограничений в задаче оптимизации.

Алгоритм CLASP демонстрирует логарифмическую зависимость от времени $T$ как для сожаления (regret), так и для кумулятивного нарушения ограничений второго рода (Cumulative Constraint Violation 2, CCV2) при использовании с сильно выпуклыми функциями потерь. В частности, достигнуты границы $O(log\ T)$ для обеих метрик, что является новым результатом в области Constrained Online Convex Optimization (COCO). Предыдущие алгоритмы не обеспечивали подобные логарифмические границы для CCV2 в случае сильно выпуклых функций потерь, что делает CLASP значительным шагом вперед в данной области.

Алгоритм CLASP демонстрирует достижение кумулятивного нарушения ограничений 2 (CCV2) порядка $O(T^(1-β))$ при работе с выпуклыми функциями потерь. Значение β определяется свойствами решаемой задачи и может варьироваться, но данный результат представляет собой значимый прогресс в области онлайн-оптимизации с ограничениями, особенно в сценариях, где строгие гарантии на нарушение ограничений необходимы. Это позволяет алгоритму CLASP эффективно справляться с задачами, где минимизация потерь должна быть сбалансирована с соблюдением заданных ограничений.

COCO: Альтернативы и будущие направления

Для преодоления ограничений, присущих классическому Online Convex Optimization (OCO), были разработаны альтернативные алгоритмы, расширяющие его возможности. Среди них выделяется Rectified Online Optimization (RECOO), который корректирует прогнозы на основе нарушений ограничений, обеспечивая более стабильное поведение в сложных условиях. Алгоритм AdaGrad, известный своей адаптивностью к различным параметрам, также применяется для решения задач с ограничениями, динамически регулируя скорость обучения для каждого параметра. Кроме того, алгоритм Switch предлагает инновационный подход, переключаясь между различными стратегиями оптимизации в зависимости от текущего состояния системы. Эти методы, в отличие от базового OCO, позволяют находить решения, удовлетворяющие заданным ограничениям, что делает их ценным инструментом для широкого спектра приложений, от управления ресурсами до машинного обучения с ограничениями.

В рамках COCO (Constrained Combinatorial Optimization) фреймворка, альтернативные алгоритмы, такие как RECOO, AdaGrad и Switch, предлагают разнообразные подходы к решению сложной задачи балансировки между оптимизацией целевой функции и соблюдением заданных ограничений. В отличие от стандартного OCO, эти методы используют различные стратегии адаптации параметров и штрафных функций, что позволяет им более эффективно справляться с задачами, где ограничения играют критическую роль. Например, RECOO использует ректификацию для корректировки нарушений ограничений, в то время как AdaGrad адаптирует скорость обучения для каждого параметра, основываясь на истории градиентов. Подобные инновации расширяют возможности COCO, позволяя находить более качественные решения в широком спектре сложных оптимизационных задач, особенно там, где традиционные подходы оказываются неэффективными из-за жестких ограничений и высокой сложности пространства поиска.

Перспективные исследования в области онлайн-оптимизации сосредотачиваются на создании гибридных подходов, объединяющих сильные стороны алгоритма CLASP с преимуществами других методов. Такой симбиоз позволит не только повысить эффективность решения сложных задач, но и обеспечить большую устойчивость к различным типам ограничений и шумам в данных. В частности, комбинирование CLASP с алгоритмами, эффективно справляющимися с нелинейными ограничениями или требующими меньшего объема вычислительных ресурсов, может привести к значительному прорыву в областях, где требуется быстрая адаптация к изменяющимся условиям, например, в робототехнике или управлении сложными системами. Подобные гибридные системы, использующие лучшие качества каждого алгоритма, представляются наиболее перспективным направлением для дальнейшего развития онлайн-оптимизации и расширения области её применения.

В представленной работе исследуется алгоритм CLASP, предназначенный для онлайн-оптимизации с динамическими ограничениями. Стремление к теоретической элегантности и практической эффективности, наблюдаемое в данной статье, перекликается с известной мыслью Дональда Кнута: «Оптимизация преждевременна». Авторы, фокусируясь на достижении логарифмических границ как для сожаления, так и для кумулятивного нарушения ограничений, демонстрируют зрелость подхода. Подобно тому, как Кнут призывает избегать преждевременной оптимизации, данное исследование показывает, что истинное совершенство достигается не в усложнении модели, а в изящном решении сложной задачи с учётом всех ограничений.

Что дальше?

Алгоритм CLASP, представленный в данной работе, демонстрирует улучшение в управлении динамическими ограничениями при онлайн-обучении. Однако, абстракции стареют. Гарантии логарифмической скорости сходимости — это, конечно, хорошо, но реальные задачи часто не укладываются в гладкие выпуклые формы. Требуется исследование устойчивости алгоритма к шумам и неточностям в данных, а также к нарушениям предположений о структуре ограничений.

Каждая сложность требует алиби. Простое расширение алгоритма для работы с невыпуклыми функциями потерь — недостаточно. Необходимо понимать, какие компромиссы возникают при ослаблении предположений о выпуклости, и как эти компромиссы влияют на практическую применимость. Более того, текущий анализ сосредоточен на теоретических границах. Эмпирическая проверка и сравнение с существующими методами на разнообразных наборах данных — критически важны.

В конечном счете, принципы остаются. Будущие исследования должны быть направлены на разработку более общих и робастных алгоритмов онлайн-оптимизации, способных адаптироваться к изменяющимся условиям и неопределенностям. Простое стремление к более низким границам сожаления — путь в никуда. Важнее — понимание фундаментальных ограничений онлайн-обучения и разработка методов, которые позволяют эффективно справляться с этими ограничениями.

Оригинал статьи: https://arxiv.org/pdf/2601.16072.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-23 18:43