Оптимальный транспорт на финансовых рынках: новый подход к ценообразованию и хеджированию

Автор: Денис Аветисян

Исследование предлагает эффективный метод для расчета цен и управления рисками сложных финансовых деривативов, основанный на теории оптимального транспорта и ускоренный с помощью GPU.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал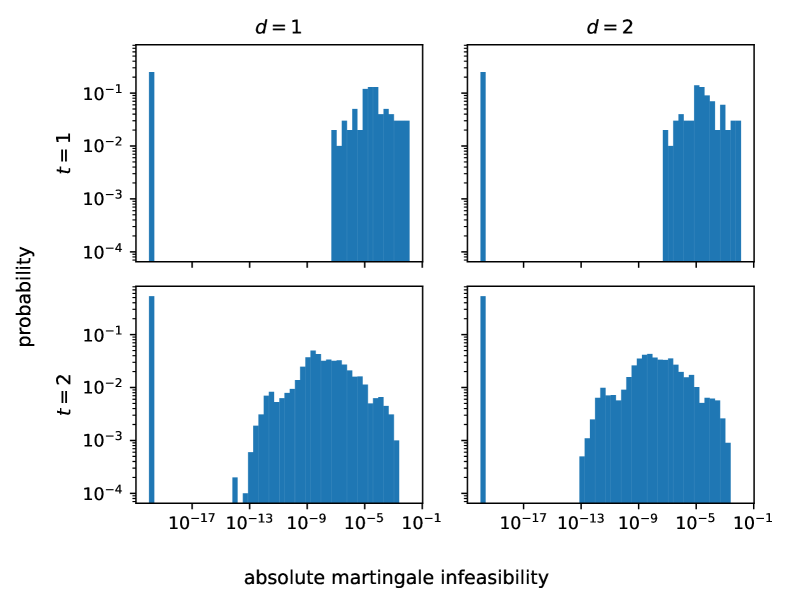

В решении 22-мерной задачи MOT за 33 временных шага, решатель PDLP в cuOpt демонстрирует устойчивое соблюдение зависящих от пути мартингальных ограничений, поддерживая невыполнимость ниже погрешности дискретизации сетки, что свидетельствует о надежности алгоритма в сложных оптимизационных задачах.

В работе доказано существование двойственных решений для многопериодной многоактивной задачи мартингального оптимального транспорта и представлена реализация на основе линейного программирования с GPU-ускорением.

Несмотря на развитый математический аппарат ценообразования и хеджирования, задача надежной оценки и управления рисками сложных финансовых деривативов в условиях неопределенности остается сложной. В данной работе, посвященной исследованию ‘Dual Attainment in Multi-Period Multi-Asset Martingale Optimal Transport and Its Computation’, доказано существование двойственных оптимизаторов для многопериодной, многоактивной задачи мартингального оптимального транспорта. Полученные теоретические результаты, подкрепленные численными экспериментами с использованием алгоритмов линейного программирования, позволяют обосновать устойчивые методы ценообразования и хеджирования, особенно в контексте производных инструментов с зависимостью от траектории. Возможно ли дальнейшее расширение области применения мартингального оптимального транспорта для решения задач управления портфелем в условиях высокой размерности и неполной информации?

От Теории к Финансам: Необходимость Надёжной Оценки

Традиционные финансовые модели зачастую опираются на упрощающие предположения, что может приводить к неверной оценке и ошибкам в хеджировании, особенно при работе со сложными производными финансовыми инструментами. Эти модели, стремясь к математической элегантности и удобству расчетов, нередко игнорируют реальные рыночные нюансы, такие как транзакционные издержки, неликвидность и влияние действий других участников рынка. Например, предположение о нормальном распределении доходности активов, широко используемое в моделях ценообразования опционов, часто не соответствует действительности, особенно в периоды рыночной турбулентности, что приводит к недооценке рисков и потенциальным убыткам. В результате, полагаясь исключительно на упрощенные модели, участники рынка могут столкнуться с существенными расхождениями между теоретической стоимостью производных инструментов и их фактической рыночной ценой, что требует разработки более надежных и точных методов оценки.

Традиционные методы оценки деривативов, опирающиеся на упрощающие предположения, зачастую оказываются недостаточными для адекватного отражения рыночной реальности и эффективного управления рисками. Неспособность этих подходов учитывать сложность финансовых инструментов и взаимодействие множества базовых активов требует разработки принципиально новой, не зависящей от конкретных моделей, системы оценки. Такая система должна обеспечивать надежную оценку стоимости деривативов и точное определение рисков, независимо от используемых теоретических построений, что особенно важно в условиях высокой волатильности и непредсказуемости финансовых рынков. Создание подобной системы — необходимое условие для стабильности финансовой системы и защиты инвесторов от необоснованных потерь, ведь она позволит минимизировать влияние погрешностей, возникающих при использовании упрощенных моделей.

Традиционные методы ценообразования деривативов зачастую оказываются неадекватными при работе с несколькими базовыми активами и сложными структурами выплат. Это связано с тем, что классические модели, как правило, опираются на предположения о независимости активов и линейности взаимосвязей, которые редко соответствуют реальным рыночным условиям. Когда количество базовых активов увеличивается, а структура выплат становится более изощренной, вероятность возникновения значительных расхождений между теоретической ценой и рыночной стоимостью дериватива возрастает экспоненциально. Например, при оценке опционов на корзину активов, корреляции между этими активами играют критическую роль, и даже небольшие погрешности в оценке этих корреляций могут приводить к существенным ошибкам в ценообразовании. В подобных ситуациях, когда стандартные модели дают неточные результаты, возникает потребность в более надежных и гибких подходах, способных учитывать сложность реальных финансовых инструментов.

Необходимость создания надежной системы ценообразования продиктована расхождением между теоретическими моделями и реальными рыночными условиями. Существующие финансовые инструменты часто опираются на упрощенные предположения, которые могут приводить к неточностям в оценке и управлении рисками, особенно в отношении сложных производных финансовых инструментов. Разрабатываемый подход направлен на согласование теоретической строгости с практическими ограничениями рынка, что позволит преодолеть разрыв между идеализированными моделями и их применением в реальной торговле. Такая система позволит учитывать множество факторов, влияющих на цену активов, и обеспечить более точную оценку рисков, что особенно важно для институциональных инвесторов и трейдеров, стремящихся к стабильной и предсказуемой прибыли. Она должна обеспечивать надежность даже в условиях волатильности и непредсказуемости, характерных для современных финансовых рынков.

Мартингальный Оптимальный Транспорт: Строгий Фундамент

Мартингальный оптимальный транспорт (MOT) представляет собой строгий математический аппарат для оценки и хеджирования финансовых деривативов, основанный на минимальном наборе предположений. В отличие от традиционных моделей, требующих сильных допущений о динамике рынка, MOT использует принципы оптимального транспорта и мартингальных ограничений для обеспечения согласованности цен с принципами нейтральности к риску. Это позволяет строить модели, которые не зависят от конкретных предположений о распределении вероятностей базовых активов, а опираются на наблюдаемые рыночные данные и требования отсутствия арбитража. $\mathbb{E}[\xi] = 0$ является ключевым требованием, обеспечивающим мартингальность и, следовательно, корректность оценки.

Мартингальное оптимальное транспортное (MOT) обеспечивает согласованность с принципами нейтрального к риску оценивания, объединяя теорию оптимального транспорта с мартингальными ограничениями. В классической финансовой математике нейтральность к риску требует, чтобы ожидаемая доходность любого актива в нейтральном к риску мире была равна безрисковой ставке. MOT формализует это требование, встраивая мартингальные ограничения непосредственно в задачу оптимального транспорта. Это гарантирует, что полученные меры эквивалентны нейтральной к риску мере, и, следовательно, цены активов, полученные с использованием MOT, соответствуют принципам безрискового хеджирования и справедливой оценки. Фактически, задача оптимального транспорта становится способом найти наиболее эффективный способ перемещения вероятностей между исходным распределением и распределением, соответствующим нейтральному к риску миру, при соблюдении мартингальных ограничений.

Транспортная задача оптимального переноса (ОТП) в классической постановке направлена на нахождение наиболее экономичного способа переноса «массы» из одного распределения вероятностей в другое. Мартингальная оптимальная транспортная задача (МОТП) расширяет эту концепцию, вводя одновременно ограничения на маргинальные распределения и мартингальные свойства. Это позволяет моделировать не только перенос массы между распределениями, но и требование, чтобы процесс переноса был согласован с принципами безрисковой оценки активов. В отличие от классической ОТП, где ограничения ограничиваются только маргинальными распределениями, МОТП учитывает динамику цен активов, обеспечивая согласованность между переносом массы и временной структурой цен, что делает ее более подходящей для финансового моделирования. Ограничения мартингальности гарантируют, что ожидаемая доходность от переноса массы равна безрисковой ставке, что является ключевым требованием для корректного ценообразования деривативов.

Ключевым компонентом Мартингального Оптимального Транспорта (МОТ) является гарантия достижения двойственности (Dual Attainment), что обеспечивает существование явных стратегий хеджирования с использованием торгуемых инструментов. Достижение двойственности означает, что задача максимизации полезности в МОТ имеет решение, которое может быть реализовано на рынке с использованием доступных активов. Это существенно, поскольку позволяет строить точные и реализуемые стратегии хеджирования, минимизирующие риск для инвестора. В рамках МОТ, двойственность гарантируется при определенных условиях, включая предположения о структуре рыночных цен и допустимости стратегий, что позволяет получить конкретные формулы для вычисления хеджирующих позиций и оценки их эффективности. $\exists \, \mu \in \mathcal{P}(X) \, \text{such that} \, \langle \mu, c \rangle = \in f_{\nu \in \mathcal{P}(X)} \langle \nu, c \rangle$ .

Дискретные маргинальные распределения, масштабированные на спотовые цены на момент времени [latex]t_0[/latex], используются в качестве входных данных для задачи MOT в 22-мерном пространстве и 33 временных шага. — Дискретные маргинальные распределения, масштабированные на спотовые цены на момент времени $t_0$ , используются в качестве входных данных для задачи MOT в 22-мерном пространстве и 33 временных шага.

Масштабирование: Многоактивные и Мультимаржинальные Модели

Расширение модели оптимальной торговли (MOT) на многомаржинальную постановку позволяет обеспечить согласованное ценообразование производных инструментов, зависящих от нескольких базовых активов. В традиционной одномаржинальной модели цена определяется на основе единственного источника неопределенности. В многомаржинальном подходе, каждый базовый актив рассматривается как отдельный источник риска, что позволяет более точно моделировать сложные зависимости между ними и, следовательно, правильно оценивать производные инструменты, выплаты по которым зависят от нескольких активов. Это особенно важно для структурированных продуктов, где цена напрямую зависит от корреляции между различными базовыми активами и их совместного поведения на рынке. Использование многомаржинальной MOT обеспечивает внутреннюю согласованность ценообразования, избегая арбитражных возможностей, которые могут возникнуть при использовании менее точных методов.

Многомерное моделирование MOT (Monotone Optimal Transport) предоставляет естественный подход к построению моделей для сложных выплат, характерных для структурированных продуктов, таких как ‘Worst-of Autocallable Options’. Данные опционы выплачивают доходность, зависящую от наихудшего поведения в корзине базовых активов. Многомерный MOT позволяет последовательно моделировать зависимости между этими активами и точно оценивать выплатные функции, учитывающие сложные условия автоколла и барьерные уровни, определяющие выплаты в случае наступления неблагоприятных событий для одного или нескольких активов в корзине. Это обеспечивает более точную оценку стоимости и рисков, связанных с такими продуктами, по сравнению с традиционными моделями, не учитывающими мультимаргинальность.

Эффективное решение многомаржинальных задач, возникающих при моделировании, требует использования специализированных вычислительных инструментов. В частности, методы линейного программирования (линейное программирование) оказались эффективными для оптимизации и ценообразования сложных производных инструментов. Реализация этих методов в рамках PDLP Solver обеспечивает возможность решения крупномасштабных задач, требующих высокой точности. Использование PDLP Solver позволяет эффективно находить оптимальные решения, учитывая множество ограничений и переменных, характерных для многомаржинального моделирования, что критически важно для корректной оценки и управления рисками.

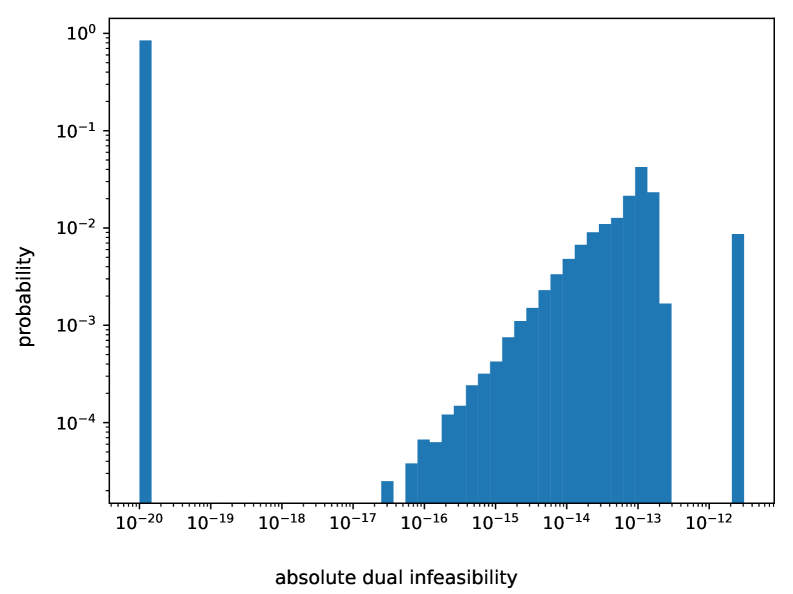
Внедрение GPU-ускорения в PDLP Solver значительно повышает скорость вычислений и масштабируемость многомаржинального моделирования оптимального транспорта (MOT). Достигнутый разрыв двойственности составляет 10^-13 или меньше, что подтверждает близость к оптимальному решению. Недопустимость первичной и двойственной задач систематически остается в пределах допустимых границ — первичная в пределах погрешности дискретизации сетки, а двойственная — в пределах заданного допуска, что демонстрирует высокую точность и способность решателя удовлетворять ограничениям.

Результаты, полученные с использованием решателя PDLP в NVIDIA cuOpt с точностью [latex]10^{-{12}}[/latex], демонстрируют низкий уровень абсолютной невыполнимости маржинальных ограничений при решении 22-мерной задачи движения (MOT) за 33 временных шага, подтверждая высокую точность обеспечения этих ограничений. — Результаты, полученные с использованием решателя PDLP в NVIDIA cuOpt с точностью $10^{-{12}}$ , демонстрируют низкий уровень абсолютной невыполнимости маржинальных ограничений при решении 22-мерной задачи движения (MOT) за 33 временных шага, подтверждая высокую точность обеспечения этих ограничений.

Соединяя Разрозненное: Практические Последствия и Перспективы Развития

Модели, основанные на теории оптимальной транспортировки (MOT), предлагают значительно более надежный и точный подход к оценке производных финансовых инструментов. В отличие от традиционных методов, которые часто полагаются на упрощающие предположения и могут быть чувствительны к небольшим изменениям в рыночных данных, MOT обеспечивает более устойчивые результаты, особенно в периоды высокой волатильности. Это, в свою очередь, приводит к улучшению управления рисками, поскольку более точная оценка позволяет более эффективно хеджировать позиции и снижать потенциальные убытки. Более того, повышенная точность оценки, обеспечиваемая MOT, позволяет финансовым учреждениям оптимизировать свои требования к капиталу, снижая тем самым затраты и повышая прибыльность. Применение MOT позволяет переосмыслить подходы к ценообразованию и управлению рисками в современной финансовой практике.

Разработанная методология открывает возможности для создания принципиально новых стратегий хеджирования, позволяющих более эффективно управлять рисками в условиях меняющейся рыночной конъюнктуры. Ранее недоступные для адекватной оценки экзотические деривативы, характеризующиеся сложной структурой выплат и высокой чувствительностью к изменениям базовых активов, теперь могут быть точно оценена и использована для диверсификации инвестиционных портфелей. Это достигается за счет более точного моделирования стохастических процессов, лежащих в основе ценообразования, и учета взаимосвязей между различными факторами риска. Возможность оценки таких инструментов не только расширяет спектр доступных финансовых продуктов, но и способствует повышению эффективности управления рисками для финансовых институтов и инвесторов.

Механизм оптимального транспорта (MOT) предоставляет уникальную возможность для сопоставления различных моделей ценообразования на финансовых рынках. Благодаря своей независимости от конкретной модели, MOT позволяет анализировать и сравнивать прогнозы, генерируемые разными подходами, выявляя их сильные и слабые стороны. Этот подход не просто сопоставляет цены, но и анализирует распределения вероятностей, что позволяет более точно оценивать риски и обнаруживать потенциальные возможности для арбитража, которые могли бы остаться незамеченными при использовании традиционных методов. В результате, MOT способствует более эффективному управлению рисками и оптимизации инвестиционных стратегий, предлагая единый язык для анализа сложных финансовых инструментов и рыночных ситуаций.

Перспективные исследования направлены на расширение области применения модели оптимальной торговли (MOT) за пределы ценообразования деривативов. В частности, изучается возможность использования MOT для оптимизации инвестиционных портфелей, где алгоритмы могут динамически корректировать распределение активов с целью максимизации прибыли при заданном уровне риска. Кроме того, MOT представляется перспективным инструментом для моделирования и оценки кредитного риска, позволяя более точно определять вероятность дефолта и устанавливать соответствующие процентные ставки. Дальнейшее развитие данной методологии может привести к созданию более эффективных стратегий управления активами и снижению финансовых рисков в различных секторах экономики, открывая новые возможности для количественного анализа и принятия решений в сфере финансов.

Решение задачи отслеживания движения (MOT) в 22 измерениях на 33 временных шага с использованием решателя PDLP в cuOpt демонстрирует незначительную абсолютную невыполнимость двойных ограничений, оставаясь в пределах допустимого допуска.

Данное исследование, устанавливающее теоретическое существование двойственных оптимизаторов для многопериодного, многоактивного мартингального оптимального транспорта, демонстрирует границы применимости существующих математических моделей в сложных финансовых системах. Подобно тому, как чёрная дыра искажает пространство-время, сложность нелинейных уравнений Эйнштейна может затмить интуицию исследователя. Как заметил Аристотель: «Нельзя знать многое о малом, пока не знаешь мало о большом». Это высказывание особенно применимо к задачам ценообразования и хеджирования сложных финансовых деривативов, где понимание общей системы необходимо для точной оценки отдельных компонентов. Успешная реализация GPU-ускоренного линейного программирования подтверждает, что даже самые сложные задачи могут быть решены при наличии достаточных вычислительных ресурсов и строгого математического подхода.

Что дальше?

Представленная работа, как и любая попытка обуздать непредсказуемость финансовых рынков, лишь обнажает границы постижимого. Доказательство существования двойственных оптимизаторов для многопериодного, многоактивного мартингального оптимального транспорта — это, несомненно, шаг вперёд. Однако, стоит помнить, что даже самое элегантное математическое решение остается лишь приближением к хаосу реальности. Ускорение вычислений на GPU позволяет решать задачи, ранее казавшиеся непосильными, но само по себе не гарантирует истинность полученных результатов.

Следующим этапом представляется не столько увеличение вычислительной мощности, сколько поиск более адекватных моделей. Текущие подходы, основанные на мартингальном транспорте, по-прежнему опираются на упрощающие предположения. Настоящим вызовом станет разработка методов, способных учитывать нелинейности, скачки и другие «неудобные» особенности финансовых временных рядов. Иначе говоря, необходимо признать, что горизонт событий знания неизбежно сужается, когда мы пытаемся смоделировать системы, чья сложность превосходит наши возможности.

В конечном счете, ценность подобных исследований заключается не в создании идеального инструмента для прогнозирования, а в осознании пределов нашего понимания. Любая теория хороша, пока свет не покидает её пределы. И, возможно, самое важное, что данная работа показывает — это необходимость постоянного переосмысления фундаментальных предпосылок, лежащих в основе финансового моделирования.

Оригинал статьи: https://arxiv.org/pdf/2602.02996.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-04 08:30