Оптимизация больших данных: новый двухэтапный алгоритм

Автор: Денис Аветисян

Исследователи предлагают инновационный подход к решению крупномасштабных задач разделяемой оптимизации, обеспечивающий более быструю сходимость даже для невыпуклых функций.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал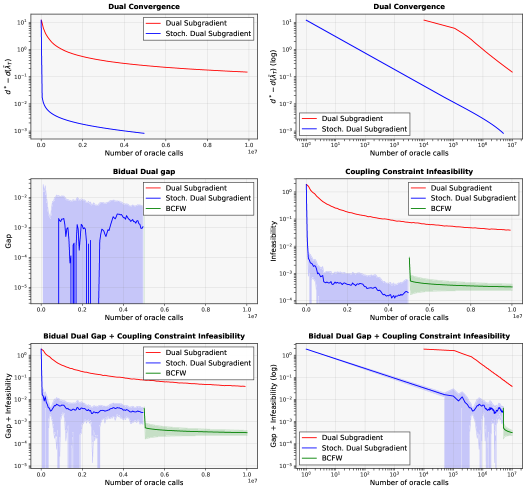

Двухэтапный алгоритм, сочетающий стохастический двойственный субградиентный метод и BCFW, демонстрирует значительное превосходство над детерминированным двойственным субградиентным алгоритмом, что подтверждается более быстрой сходимостью двойственной целевой функции, снижением бидуального разрыва и меньшим нарушением связующего ограничения, особенно заметным в логарифмической шкале, несмотря на эпизодическое нарушение связующего ограничения отдельными бидуальными итерациями.

Предложен двухэтапный стохастический алгоритм, сочетающий метод двойного субградиента и разложение Каратеодори для оптимизации при аффинных ограничениях.

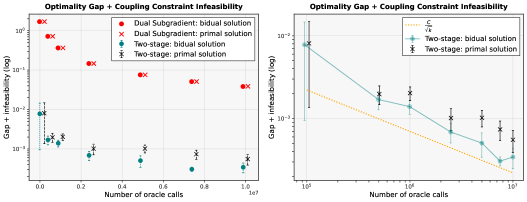
В задачах раздельной оптимизации с аффинными ограничениями, традиционные двойственные методы сталкиваются с вычислительными трудностями при увеличении числа агентов. В данной работе, посвященной алгоритму ‘Two-stage stochastic algorithm for solving large-scale (non)-convex separable optimization problems under affine constraints’, предложен двухэтапный стохастический подход, сочетающий двойственный субградиентный метод с процедурой разложения Каратаудори. Разработанный алгоритм позволяет добиться улучшения скорости сходимости как для выпуклых, так и для невыпуклых задач, требуя лишь $O(\frac{1}{\epsilon^2} + \frac{N}{\epsilon^{2/3}})$ вычислений сопряженных функций. Каковы перспективы применения предложенного алгоритма в задачах крупномасштабной оптимизации, возникающих в машинном обучении и обработке больших данных?

Временные Границы: Основы Проблемы P

Оптимизационные задачи, подобные проблеме P, широко распространены в различных областях науки и техники. В машинном обучении они применяются для настройки параметров моделей, обеспечивая максимальную точность и эффективность предсказаний. В сфере распределения ресурсов, подобные задачи позволяют оптимально использовать ограниченные средства для достижения наилучших результатов, будь то логистика, финансы или управление производством. $Задача\,P$ представляет собой общий класс проблем, где необходимо найти наилучшее решение среди множества возможных вариантов, учитывая заданные ограничения и критерии, что делает её фундаментальной для многих практических приложений.

Многие задачи оптимизации, такие как ‘Проблема P’, характеризуются значительным числом переменных и ограничений, что существенно усложняет их непосредственное решение. Увеличение количества переменных приводит к экспоненциальному росту пространства поиска, требуя огромных вычислительных ресурсов для перебора всех возможных комбинаций. Ограничения, в свою очередь, сужают это пространство, но добавляют сложность в процессе поиска допустимых решений. Даже при использовании мощных вычислительных систем, прямое решение таких задач может оказаться непосильным или занимать недопустимо долгое время, что делает необходимым разработку специализированных алгоритмов и приближенных методов для эффективного нахождения оптимальных или субоптимальных решений. Это особенно актуально в областях, где требуется обработка больших объемов данных и принятие оперативных решений.

Когда задача «P» приобретает характеристики невыпуклой задачи, стандартные методы оптимизации сталкиваются с серьезными трудностями в поиске глобально оптимальных решений. В то время как выпуклые задачи гарантируют нахождение минимума при помощи, например, градиентного спуска, невыпуклость пространства решений приводит к появлению множества локальных минимумов. Оптимизационные алгоритмы могут застревать в этих локальных минимумах, выдавая решения, далекие от истинного глобального оптимума. Это особенно критично в задачах машинного обучения, где локальный минимум может привести к значительно ухудшенной производительности модели. Поэтому, для решения невыпуклых задач требуются более сложные подходы, такие как методы Монте-Карло, эвристические алгоритмы или использование специальных техник для выхода из локальных минимумов, что существенно усложняет процесс оптимизации и требует значительных вычислительных ресурсов.

Результаты показывают, что предложенный двухэтапный алгоритм обеспечивает производительность, сопоставимую с решением бидуальной выпуклой задачи, и демонстрирует сходимость порядка обратной величины квадратного корня из числа обращений к оракулу, что подтверждает теоретические оценки, полученные в работах 3.3 и 4.5.

Двойственность и Метод Двойственного Субградиента

Формулировка двойственной задачи $D$ представляет собой преобразование исходной оптимизационной задачи в эквивалентную, но альтернативную формулировку. Это достигается путем введения лагранжевых множителей и формирования двойственной функции, максимизирующей нижнюю границу исходной задачи. Решение двойственной задачи предоставляет информацию о решении исходной, а в некоторых случаях, позволяет получить точное решение исходной задачи. Преимущество двойственного подхода заключается в возможности упрощения вычислений, особенно при наличии ограничений, а также в предоставлении оценки оптимального значения исходной задачи даже при невозможности найти точное решение.

Двойственный субградиентный метод представляет собой итеративный подход к решению двойственной задачи оптимизации. На каждой итерации переменные обновляются на основе субградиентов двойственной функции. Субградиент, в отличие от градиента, определяется для недифференцируемых функций и предоставляет направление наиболее быстрого увеличения (или уменьшения) функции в данной точке. Этот метод позволяет эффективно находить решения двойственной задачи, особенно в случаях, когда прямое решение исходной задачи затруднено или вычислительно дорого. Обновление переменных происходит по формуле $x_{k+1} = x_k - \alpha_k \partial f(x_k)$ , где $\alpha_k$ — размер шага, а $\partial f(x_k)$ — субградиент функции f в точке x_k.

Метод двойственного подъёмного градиента использует так называемый «Оракул O1» для обеспечения необходимой информации на каждой итерации процесса оптимизации. Этот оракул предоставляет значения двойственной функции и её субградиента, что позволяет эффективно обновлять переменные и ускорять сходимость алгоритма. По сути, «Оракул O1» выполняет вычисление, сложность которого не зависит от размерности задачи, что критически важно для масштабируемости метода, особенно при работе с большими объемами данных и высокоразмерными пространствами признаков. Предоставление этой информации на каждой итерации позволяет алгоритму быстро двигаться к оптимальному решению двойственной задачи $D$ .

Первоначальная вычислительная сложность метода двойственных субградиентов, выраженная как $O(N/ϵ²)$ , где N — размерность задачи, а ϵ — требуемая точность, может оказаться неприемлемо высокой для задач большого масштаба. Данная сложность указывает на то, что количество итераций, необходимых для достижения заданной точности, обратно пропорционально квадрату точности и линейно зависит от размера задачи. Следовательно, при увеличении либо размера задачи, либо требуемой точности, вычислительные затраты растут существенно, что делает применение метода непрактичным для решения крупномасштабных оптимизационных задач без дополнительных модификаций или использования альтернативных алгоритмов.

Преодоление Невыпуклости с Помощью Бидуальной Формулировки

При переходе к задачам, включающим невыпуклые компоненты (проблема P), прямое решение двойственной задачи может оказаться вычислительно сложным или даже невозможным. Невыпуклость исходной задачи приводит к тому, что двойственная задача также становится невыпуклой, что препятствует использованию стандартных методов оптимизации, гарантирующих нахождение глобального оптимума. Это обусловлено тем, что двойственная функция может иметь локальные оптимумы, которые не соответствуют глобальному оптимуму исходной задачи. В результате, стандартные алгоритмы, такие как градиентный спуск, могут застревать в локальных оптимумах двойственной функции, не находя оптимального решения для исходной невыпуклой задачи.

Бидуальная задача представляет собой дальнейшую дуализацию исходной невыпуклой задачи оптимизации. Вместо непосредственного решения двойственной задачи, которая может оказаться сложной из-за невыпуклости, формируется ее двойственная версия. Это позволяет преобразовать исходную задачу в эквивалентную, но потенциально более удобную для решения формулировку. Процесс дуализации повторяется, создавая задачу, которая, хотя и является двойственной к двойственной, может обладать лучшими свойствами с точки зрения оптимизации, например, выпуклостью или более гладкой структурой. Решение бидуальной задачи, а затем возврат к исходной задаче, обеспечивает альтернативный подход к поиску оптимальных или субоптимальных решений в условиях невыпуклости.

Разложение Каратеодори используется для приближенного решения невыпуклых задач путем представления решений в виде выпуклых комбинаций крайних точек исходного множества. Этот метод позволяет ограничить поиск решений внутри выпуклой оболочки, значительно упрощая ландшафт оптимизации. Вместо работы со всем исходным невыпуклым множеством, алгоритм фокусируется на его выпуклой оболочке, что приводит к более эффективным и стабильным алгоритмам оптимизации. $x = \sum_{i=1}^{n+1} \alpha_i x_i$ , где $\sum_{i=1}^{n+1} \alpha_i = 1$ и $\alpha_i \ge 0$ , демонстрирует представление точки x как выпуклую комбинацию точек $x_i$ .

Метод усреднения итераций на этапе решения, известный как “Усредненные Итерации”, позволяет улучшить качество конечного решения, особенно в задачах, где прямое решение затруднено. Суть подхода заключается в вычислении среднего значения нескольких последовательных приближений, полученных на этапе решения исходной задачи. Математически, это можно представить как $\bar{x}_k = \frac{1}{K} \sum_{i=1}^{K} x_i$ , где $x_i$ — $i$ -я итерация, а $K$ — количество итераций, используемых для усреднения. Практически, усреднение снижает влияние случайных колебаний и позволяет получить более стабильное и точное решение, особенно в контексте невыпуклых задач оптимизации.

Двухэтапный Подход: Повышенная Эффективность и Сложность

Двухэтапный подход базируется на методе двойственного градиентного спуска, существенно расширяя его возможности за счет внедрения стохастических оценок, реализуемых посредством метода ‘Стохастического двойственного градиентного спуска’. Вместо точного вычисления градиентов, данный подход использует случайные выборки данных для их аппроксимации, что позволяет значительно ускорить процесс сходимости, особенно в задачах, характеризующихся большими объемами данных и наличием шумов. Такая стохастическая аппроксимация позволяет снизить вычислительную сложность каждого шага и, в конечном итоге, добиться более эффективного решения оптимизационной задачи, сохраняя при этом приемлемую точность результата. Использование стохастических оценок является ключевым элементом, обеспечивающим преимущество данного подхода перед классическими методами двойственного градиентного спуска.

Введение стохастичности в алгоритм существенно ускоряет сходимость, особенно при решении крупномасштабных задач, характеризующихся наличием зашумленных данных. Традиционные методы часто сталкиваются с трудностями при обработке больших объемов информации и подвержены влиянию неточностей, что замедляет процесс нахождения оптимального решения. Использование случайных оценок позволяет алгоритму более эффективно исследовать пространство решений, обходя локальные минимумы и быстрее приближаясь к глобальному оптимуму. Этот подход особенно ценен в ситуациях, когда данные поступают не идеально и содержат случайные отклонения, поскольку стохастичность позволяет алгоритму «сглаживать» шум и фокусироваться на наиболее значимых закономерностях, обеспечивая стабильную и быструю сходимость даже в условиях неопределенности.

Данный подход позволил добиться значительного улучшения в ожидаемой вычислительной сложности алгоритма. Интеллектуальное сочетание стохастической оптимизации с усовершенствованными шагами для нахождения примального решения привело к достижению сложности, выражаемой как $O(1/ϵ² + N/ϵ²/₃)$ . В сравнении с традиционной сложностью $O(N/ϵ²)$ для методов двойственного субградиента, данное улучшение особенно заметно при работе с большими объемами данных, где параметр N, определяющий размерность задачи, играет ключевую роль. Подобное сокращение сложности позволяет решать более сложные и масштабные оптимизационные задачи, что делает его востребованным в областях, работающих с большими объемами данных.

Предложенный двухступенчатый подход демонстрирует заметное улучшение по сравнению со стандартной сложностью методов двойственного субградиента, выраженной как $O(N/ϵ²)$ . В случаях, когда размер задачи, обозначенный как N, становится существенно большим, преимущества нового метода особенно ощутимы. Уменьшение вычислительных затрат позволяет решать более сложные и масштабные оптимизационные задачи, что делает его востребованным в областях, работающих с большими объемами данных.

Представленная работа исследует методы оптимизации, направленные на решение масштабных задач с аффинными ограничениями. Особое внимание уделяется достижению более высоких скоростей сходимости, что критически важно для практического применения алгоритмов в условиях ограниченных ресурсов. Как отмечал Альберт Эйнштейн: «Самое главное — это задавать правильные вопросы». В данном исследовании, вопрос о скорости сходимости решен путем комбинирования стохастических двойственных субградиентных методов с разложением Каратеодори, что позволяет эффективно справляться со сложностями невыпуклых задач разделяемой оптимизации. Это подтверждает, что даже в сложных системах, тщательно сформулированный подход может привести к значительному прогрессу.

Что впереди?

Представленный подход, несомненно, добавляет ещё один слой абстракции к уже существующему арсеналу методов решения задач разделяемой оптимизации. Однако, как и любая абстракция, он несёт в себе груз прошлого — предположения о структуре данных, ограничения на аффинные ограничения, и, в конечном счёте, неизбежную зависимость от выбора шага. Вопрос не в том, насколько быстро сходится алгоритм в идеальных условиях, а в том, как грациозно он деградирует в реальном мире, где данные далеки от совершенства.

Очевидным направлением для дальнейших исследований представляется расширение класса аффинных ограничений. Каждая система стареет, и алгоритм, ограниченный жесткими рамками, обречён на преждевременную потерю актуальности. Вместо того чтобы стремиться к максимальной скорости сходимости в узком диапазоне задач, стоит обратить внимание на устойчивость к непредсказуемым изменениям в структуре данных и ограничениях.

В конечном счёте, истинное достоинство любого алгоритма определяется не его способностью решать текущие задачи, а его потенциалом к адаптации. Медленные изменения — вот что обеспечивает устойчивость. Вместо того, чтобы изобретать принципиально новые методы, возможно, стоит сосредоточиться на разработке механизмов самонастройки и адаптации существующих, позволяющих алгоритму плавно эволюционировать вместе с изменяющейся средой.

Оригинал статьи: https://arxiv.org/pdf/2602.06637.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-10 05:55