Оптимизация на грани: новый подход к решению задач покрытия множества

от

Автор: Денис Аветисян

В статье представлена инновационная стратегия ‘dual-path fixing’, позволяющая существенно повысить эффективность алгоритмов поиска оптимальных решений в задачах целочисленного линейного программирования.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал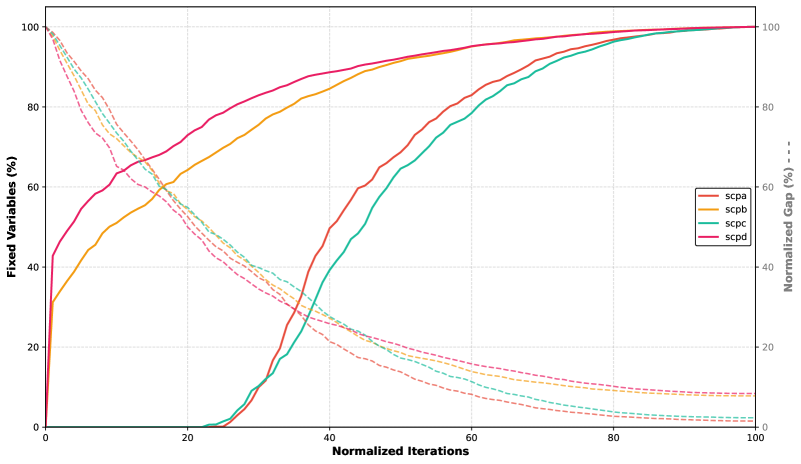
Поведение алгоритма DPF, продемонстрированное в итерациях симплекс-метода на наборах данных Бисли A-D, демонстрирует его способность к адаптации и оптимизации в условиях меняющейся сложности задачи.
Поведение алгоритма DPF, продемонстрированное в итерациях симплекс-метода на наборах данных Бисли A-D, демонстрирует его способность к адаптации и оптимизации в условиях меняющейся сложности задачи.

Предлагаемая техника ‘dual-path fixing’ использует последовательность двойственно допустимых решений для усиления фиксации переменных в процессе релаксации, улучшая стандартные методы фиксации на основе reduced-cost.

Эффективное фиксирование целочисленных переменных остается сложной задачей в алгоритмах решения задач смешанного целочисленного программирования. В данной работе, посвященной ‘The dual-path fixing strategy and its application to the set-covering problem’, предложена новая стратегия — «фиксирование по двойственному пути», использующая последовательность двойственно допустимых решений для усиления процесса фиксирования. Предложенный подход демонстрирует потенциал превзойти стандартное фиксирование по сниженным затратам, требуя при этом вычислительных затрат, сопоставимых с базовыми двойственными алгоритмами. Способно ли данное улучшение стратегии фиксирования существенно повысить эффективность алгоритмов типа ветвей и границ при решении реальных задач, таких как задача о покрытии множества?

Неизбежность Дискретности: Вызовы Целочисленного Программирования

Многие задачи оптимизации, возникающие в реальной жизни, требуют использования целочисленных переменных для точного моделирования дискретных решений. Классический пример — задача о покрытии множества, где необходимо выбрать минимальное количество подмножеств, покрывающих все элементы универсального множества; выбор каждого подмножества представляется бинарной (0 или 1) переменной. Подобные задачи возникают в логистике, планировании производства, распределении ресурсов и многих других областях. Использование целочисленных переменных позволяет корректно отразить суть проблемы, где, например, невозможно выбрать “половину” транспортного средства или произвести “часть” товара. Отказ от целочисленности привел бы к нереалистичным и, следовательно, бесполезным решениям, даже если бы алгоритм работал быстро.

Прямое решение задач смешанного целочисленного линейного программирования (MILP) представляет собой значительную вычислительную проблему, сложность которой экспоненциально возрастает с увеличением масштаба задачи. Это обусловлено тем, что поиск оптимального решения требует перебора огромного количества возможных комбинаций целочисленных переменных, что делает полный перебор непрактичным даже для задач умеренного размера. В то время как алгоритмы линейного программирования могут эффективно решать задачи с непрерывными переменными, добавление целочисленных ограничений вводит дискретность в пространство решений, радикально увеличивая время, необходимое для достижения оптимальности. По мере роста числа переменных и ограничений, вычислительные затраты быстро становятся непомерными, требуя разработки специализированных алгоритмов и эвристик для приближенного решения сложных MILP-задач.

Традиционные методы оптимизации, разработанные для работы с непрерывными переменными, испытывают значительные трудности при решении задач, включающих целочисленные ограничения. Суть проблемы заключается в экспоненциальном росте сложности пространства решений при добавлении даже небольшого количества целочисленных переменных. Вместо гладкой поверхности, которую легко исследовать, возникает дискретный ландшафт с множеством локальных оптимумов и разрывов, что делает стандартные алгоритмы неэффективными. Поиск глобального оптимума в таком пространстве требует значительных вычислительных ресурсов и времени, поскольку алгоритмы вынуждены перебирать множество комбинаций, а не плавно двигаться к оптимальному решению, как в случае с непрерывными задачами. В результате, даже относительно небольшие задачи целочисленного программирования могут оказаться непосильными для классических методов оптимизации.

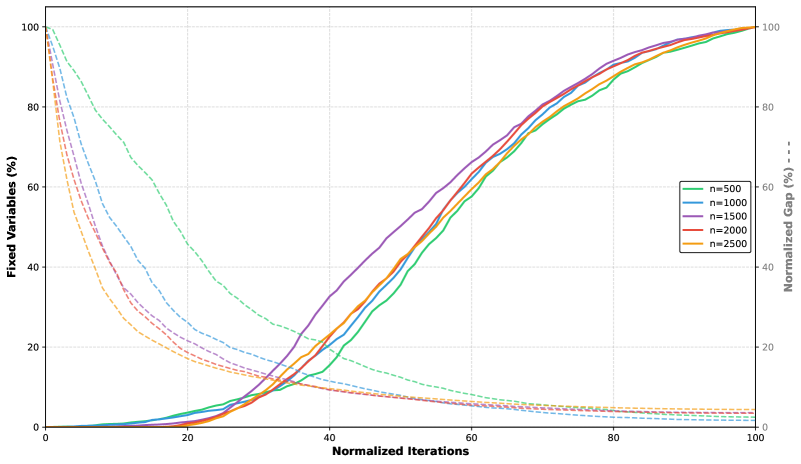
Сравнение итеративных процедур показывает, что исходная задача с [latex]n=1000[/latex] и [latex]m=7585[/latex] успешно решается.
Сравнение итеративных процедур показывает, что исходная задача с n=1000 и m=7585 успешно решается.

Упрощение Сложного: Методы Релаксации и Фиксации

Непрерывная релаксация — это стандартный метод упрощения задач целочисленного программирования. Суть подхода заключается во временном снятии ограничений целочисленности с переменных, что позволяет преобразовать исходную задачу в более простую задачу непрерывной оптимизации. Вместо поиска решения, удовлетворяющего целочисленным ограничениям, решается задача, где переменные могут принимать любые вещественные значения. Решение полученной непрерывной задачи служит отправной точкой для последующих алгоритмов, направленных на восстановление целочисленности и нахождение допустимого решения исходной задачи. Такой подход позволяет использовать эффективные методы непрерывной оптимизации для получения приближенного решения, которое затем уточняется.

После получения решения релаксированной (непрерывной) задачи, методы пониженной стоимости (Reduced-Cost Fixing) и сильной фиксации (Strong Fixing) используются для определения целочисленных переменных, которые можно зафиксировать на своих оптимальных целочисленных значениях. Метод пониженной стоимости анализирует двойственные переменные, связанные с ограничениями целочисленности, и фиксирует переменные, для которых стоимость изменения их значения на единицу слишком высока. Сильная фиксация, напротив, использует информацию о границах целочисленных переменных и их текущих значениях в решении релаксированной задачи, чтобы определить, какие значения допустимы и могут быть зафиксированы без ухудшения оптимальности решения. Оба метода позволяют сократить область поиска в исходной целочисленной задаче, приближая решение к выполнимости и повышая эффективность алгоритмов оптимизации.

Методы фиксации переменных, такие как фиксация по сниженной стоимости и сильная фиксация, используют информацию, полученную при релаксации целочисленной задачи, для уменьшения области поиска допустимых решений. После решения релаксированной задачи с непрерывными переменными, анализируется информация о значениях двойственных переменных и сниженной стоимости. Если сниженная стоимость переменной показывает, что изменение её значения не улучшит целевую функцию, а двойственная переменная указывает на отсутствие влияния на оптимальность, то данную переменную можно зафиксировать на её текущем значении без потери оптимальности. Это позволяет исключить данную переменную из дальнейшего рассмотрения, упрощая задачу и приближая поиск к целочисленному решению исходной задачи.

В среднем, наблюдается снижение количества переменных (экземпляров SLS).
В среднем, наблюдается снижение количества переменных (экземпляров SLS).

Систематический Поиск: Алгоритмы Ветвей и Границ и Двойственные Подходы

Метод ветвей и границ (Branch-and-Bound) представляет собой мощный точный алгоритм, предназначенный для решения задач математического программирования с целочисленными ограничениями (MILO). В основе алгоритма лежит систематическое исследование пространства решений путем рекурсивного разбиения исходной задачи на более мелкие подзадачи. Каждая подзадача представляет собой ограничение исходной задачи, что позволяет исключать из рассмотрения целые ветви пространства решений, не содержащие оптимальное решение. Процесс продолжается до тех пор, пока не будет найдено оптимальное решение или доказано, что его не существует в исследуемом подпространстве. Эффективность метода зависит от стратегии выбора переменных для ветвления и от использования эвристик для оценки границ, позволяющих отсекать неперспективные подзадачи.

В алгоритме ветвей и границ (Branch-and-Bound) эффективность поиска существенно повышается за счет использования стратегий выбора переменных для ветвления, таких как “сильное ветвление” (Strong Branching). Данный подход заключается в оценке эффективности ветвления по различным переменным, основанной на критериях, таких как псевдо-затраты или влияние на целевую функцию. Выбор переменной, приводящей к наибольшему потенциальному улучшению, позволяет сократить количество исследуемых подзадач и, следовательно, ускорить процесс нахождения оптимального решения. Применение стратегий сильного ветвления позволяет более эффективно управлять поисковым деревом, избегая исследования неперспективных областей пространства решений.

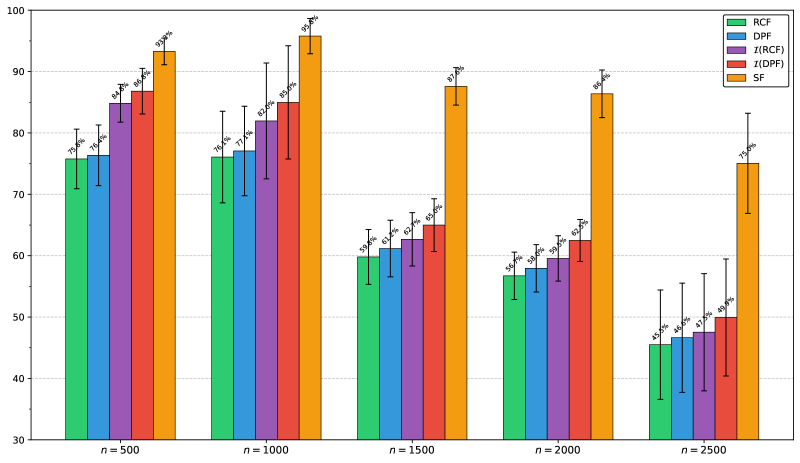
Внедрение метода Dual-Path Fixing (DPF) в сочетании с алгоритмом Dual Simplex и использованием двойственной допустимости (Dual Feasibility) позволяет добиться в среднем улучшения на 1.4% в количестве фиксированных переменных при решении задач покрытия множествами (set-covering instances). Данное улучшение достигается по сравнению с использованием метода фиксации на основе приведенных затрат (reduced-cost fixing). DPF эффективно идентифицирует и фиксирует переменные, используя информацию о двойственных решениях, что приводит к сокращению размера исследуемого пространства решений и повышению эффективности алгоритма Branch-and-Bound.

В процессе итераций симплекс-метода наблюдается характерное поведение DPF (Dynamic Programming Formulation) для экземпляров SLS (Sequential Local Search).
В процессе итераций симплекс-метода наблюдается характерное поведение DPF (Dynamic Programming Formulation) для экземпляров SLS (Sequential Local Search).

Расширение Горизонтов: Применение к MINLO и Сила Обобщения

Методы непрерывной релаксации, фиксации переменных и ветвей и границ, успешно применяемые в решении задач целочисленного программирования, могут быть расширены для работы с более сложным классом задач — задачами смешанного целочисленного нелинейного программирования (MINLO). Расширение этих техник позволяет решать оптимизационные задачи, включающие как целочисленные, так и непрерывные переменные, а также нелинейные функции и ограничения. Это существенно расширяет область применения данных алгоритмов, позволяя находить оптимальные решения в широком спектре практических задач, где нелинейность играет важную роль, например, в задачах управления ресурсами, проектирования и планирования. Возможность адаптации известных методов к MINLO задачам представляет собой значительный шаг в развитии области оптимизации и позволяет использовать существующие инструменты для решения новых, более сложных проблем.

Методы релаксации Лагранжа представляют собой мощный инструмент для решения задач смешанного целочисленного нелинейного программирования (MINLO), позволяя эффективно обрабатывать нелинейные ограничения. В отличие от традиционных подходов, которые могут столкнуться с трудностями при работе с нелинейностями, релаксация Лагранжа преобразует исходную задачу в серию более простых подзадач, которые можно решить с использованием стандартных методов оптимизации. Этот подход позволяет значительно расширить применимость техник непрерывной релаксации, фиксации и метода ветвей и границ, делая их эффективными для более широкого класса сложных оптимизационных задач, где нелинейные зависимости играют ключевую роль.

Исследование продемонстрировало эффективность предложенного подхода на крупномасштабной задаче оптимизации, включающей 1000 переменных и 7585 ограничений. В ходе решения, методика DPF (Disjunctive Programming Formulation) позволила зафиксировать 845 переменных, значительно упростив задачу и снизив вычислительную сложность. Полученные результаты свидетельствуют о существенном потенциале для повышения производительности и масштабируемости алгоритмов оптимизации, особенно при работе с задачами, характеризующимися большим количеством переменных и ограничений. Фиксация столь значительного числа переменных указывает на возможность существенного сокращения пространства поиска оптимального решения, что особенно важно для сложных нелинейных задач.

Исследование, представленное в данной работе, демонстрирует стремление к оптимизации сложных систем, что не может не напомнить высказывание Макса Планка: «В науке нет ничего абсолютного, все относительно». В контексте предложенной стратегии ‘dual-path fixing’, наблюдается попытка улучшить существующие методы решения задач, таких как ‘set-covering problem’, за счет более эффективного использования информации о двойственных решениях. Авторы, по сути, признают, что статичные подходы рано или поздно достигают своего предела, и необходим постоянный поиск новых путей к оптимизации. Это созвучно идее о том, что любая система стареет, и лишь способность к адаптации позволяет ей сохранять функциональность в изменяющихся условиях. Подобный подход, где ключевым является не мгновенный результат, а способность к непрерывному совершенствованию, является признаком зрелости и дальновидности.

Куда же дальше?

Представленная работа, касающаяся стратегии двойного пути фиксации, неизбежно ставит вопрос о природе самой фиксации в задачах целочисленного линейного программирования. Каждая зафиксированная переменная — это не триумф алгоритма, а скорее, признание его временных ограничений. Двойной путь, выявляя последовательность двойственно допустимых решений, лишь отсрочивает неизбежное — приближение к границе допустимой области, где окончательные решения обречены на появление. Важно понимать, что совершенство фиксации — иллюзия, а каждый сбой — сигнал времени, указывающий на необходимость рефакторинга.

Очевидным направлением дальнейших исследований представляется адаптация предложенного подхода к более сложным классам задач, где структура ограничений не столь благосклонна к последовательному уточнению. Стоит рассмотреть возможность интеграции двойного пути с эвристическими методами, позволяющими “обходить” области, где фиксация неэффективна. Рефакторинг — это диалог с прошлым, и в данном контексте — это постоянный поиск компромисса между точностью и вычислительной сложностью.

В конечном счете, задача оптимизации — это не поиск идеального решения, а построение достаточно хорошей модели, способной выдержать испытание временем. И каждая новая стратегия, подобно двойному пути фиксации, лишь добавляет еще один слой в эту сложную и бесконечно увлекательную конструкцию.

Оригинал статьи: https://arxiv.org/pdf/2601.20977.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-31 13:32