Оптимизация на многообразиях Стифеля: новый подход к поиску решений

Автор: Денис Аветисян

В статье представлен эффективный метод штрафных функций для решения задач оптимизации на обобщенных многообразиях Стифеля, превосходящий традиционные методы римановой оптимизации.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал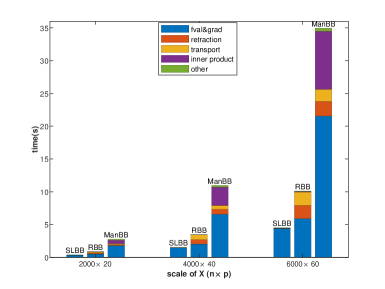

Время работы центрального процессора в различных частях алгоритма демонстрирует зависимость от масштаба решаемой задачи, что указывает на необходимость оптимизации для эффективной обработки данных различного объема.

Разработанный метод SLEP демонстрирует эквивалентность исходной задаче и обеспечивает превосходную производительность, особенно в задачах, требующих разреженности.

Оптимизационные задачи на обобщённых многообразиях Стифеля часто сталкиваются с трудностями при наличии сингулярных матриц, ограничивающих применимость существующих методов. В данной работе, посвященной исследованию ‘A Smooth Locally Exact Penalty Method for Optimization Problems over Generalized Stiefel Manifolds’, предложен новый метод штрафных функций (SLEP), эквивалентный исходной задаче в аспекте стационарных точек. Данный подход позволяет избежать вычислительно затратных операций вроде ретракций и векторных транспортов, характерных для римановой оптимизации, снижая стоимость каждой итерации. Может ли предложенный метод стать эффективным инструментом для решения широкого класса задач, включая канонический корреляционный анализ и расчеты в электронной структуре?

Обобщенные Ортогональные Ограничения: Основа Сложности и Возможностей

Многие задачи машинного обучения, от анализа изображений до обработки естественного языка, могут быть представлены в виде оптимизационных задач с обобщенными ортогональными ограничениями (ООО). Этот подход предоставляет мощный инструмент для моделирования сложных взаимосвязей между переменными, обеспечивая возможность нахождения оптимальных решений при соблюдении заданных условий. Однако, несмотря на свою эффективность, формулировка задач в терминах ООО приводит к появлению нетривиальной математической структуры, требующей разработки специализированных алгоритмов для ее эффективного решения. Суть заключается в необходимости оптимизации на обобщенном многообразии Штифеля, характеризующемся сложной геометрией, что делает стандартные методы оптимизации неэффективными и стимулирует поиск инновационных подходов к решению подобных задач.

Непосредственное решение задач оптимизации с обобщенными ортогональными ограничениями (ООР) представляет собой серьезную вычислительную проблему из-за сложной геометрии обобщенного многообразия Штифеля. Это многообразие, представляющее собой обобщение привычного многообразия Штифеля, характеризуется нетривиальной структурой, в которой стандартные методы оптимизации часто сталкиваются с трудностями. Особенность заключается в том, что поиск решений на этом многообразии требует учета не только ортогональности, но и дополнительных ограничений, что существенно усложняет вычисления и требует разработки специализированных алгоритмов. $\mathbb{S}^{m,k} = \{X \in \mathbb{R}^{m \times k} : X^T X = I \}$ — типичное представление обобщенного многообразия Штифеля, где $I$ — единичная матрица. Сложность заключается в поддержании условий, определяющих это многообразие, на протяжении всего процесса оптимизации, что требует значительных вычислительных ресурсов и времени.

Современные задачи оптимизации с обобщенными ортогональными ограничениями (ООС) зачастую характеризуются колоссальными объемами данных и сложностью взаимосвязей, что ставит традиционные методы решения на грань вычислительной неэффективности. Алгоритмы, успешно применявшиеся ранее, демонстрируют существенное замедление и потерю точности при увеличении размерности пространства поиска и числа ограничений. Это обусловлено экспоненциальным ростом вычислительных затрат, связанных с поддержанием ортогональности на протяжении всего процесса оптимизации. В связи с этим, активно разрабатываются инновационные подходы, включающие использование стохастических методов, аппроксимаций низкого ранга и специализированных алгоритмов, адаптированных к структуре обобщенного многообразия Стифеля $\mathcal{S}$ , чтобы обеспечить масштабируемость и приемлемое время вычислений для решения сложных задач ООС в различных областях, от машинного обучения до обработки сигналов.

Переформулировка с Помощью Метода Плавных Штрафных Функций

Модель Smooth Locally Exact Penalty (SLEP) представляет собой эффективную переформулировку задачи оптимального управления (OCP) в задачу безусловной оптимизации, что значительно упрощает вычислительную сложность. Вместо решения задачи с ограничениями, SLEP преобразует её в эквивалентную задачу, где целевая функция модифицируется добавлением штрафного члена, который стремится к нулю при выполнении ограничений. Такая переформулировка позволяет применять стандартные методы безусловной оптимизации, которые, как правило, более разработаны и эффективны, чем методы, предназначенные для работы с ограничениями. Данный подход позволяет избежать необходимости вычисления проекций на допустимое множество, что снижает вычислительные затраты и повышает скорость сходимости алгоритма.

Модель Smooth Locally Exact Penalty (SLEP) использует параметр штрафа для управления компромиссом между минимизацией исходной целевой функции и приблизительным удовлетворением ограничений. Увеличение значения параметра штрафа приводит к более строгому удовлетворению ограничений, но может ухудшить оптимизацию целевой функции. Напротив, уменьшение параметра штрафа позволяет более свободно оптимизировать целевую функцию, но может привести к значительному нарушению ограничений. Таким образом, выбор оптимального значения параметра штрафа является ключевым для достижения баланса между точностью и эффективностью решения задачи оптимизации.

Применение метода Smooth Locally Exact Penalty (SLEP) требует тщательной настройки параметра штрафа, определяющего баланс между минимизацией исходной целевой функции и приближенным удовлетворением ограничений. Несмотря на необходимость тонкой калибровки, полученная оптимизационная задача позволяет добиться существенных преимуществ в производительности. В частности, результаты, представленные в данной работе, демонстрируют, что применение методов оптимизации без ограничений к модели SLEP превосходит по эффективности методы, основанные на римановой геометрии, что подтверждает практическую ценность данного подхода.

Ускорение Оптимизации с Алгоритмом SLBB

Алгоритм SLBB, являясь расширением метода Барзаила-Борвейна (BB) для градиентной оптимизации, представляет собой практичное и эффективное решение для оптимизации задачи оптимального управления (OCP), реформулированной с использованием модели SLEP. В отличие от традиционных подходов, SLBB позволяет избежать вычислительных затрат, связанных с непосредственным обеспечением ортогональных ограничений, что достигается за счет специфической структуры SLEP-модели. Это обеспечивает более высокую скорость сходимости и снижает общую вычислительную сложность по сравнению с альтернативными методами оптимизации.

Алгоритм SLBB, используя модель SLEP, позволяет избежать вычислительных затрат, связанных с прямым обеспечением ортогональных ограничений. Традиционные методы оптимизации, требующие явного поддержания ортогональности, включают сложные вычисления, такие как проекции и вычисление римановых градиентов. Модель SLEP, в свою очередь, преобразует задачу оптимизации таким образом, что ортогональность обеспечивается неявно, что значительно снижает вычислительную сложность каждой итерации алгоритма. Это приводит к существенному ускорению процесса оптимизации по сравнению с методами, напрямую работающими с ортогональными ограничениями, особенно в задачах большого масштаба.

Численные эксперименты показали, что алгоритм SLBB стабильно превосходит римановы методы, такие как ManBB и RBB, по времени выполнения CPU. Снижение вычислительной стоимости одной итерации SLBB по сравнению с римановыми методами обусловлено избежанием дорогостоящих операций, включая вычисление римановых градиентов. Это позволяет SLBB демонстрировать более высокую скорость сходимости при решении задач оптимизации, особенно в контексте SLEP-переформулированной задачи оптимального управления.

Разреженность и Эффективность в Каноническом Корреляционном Анализе

Метод разреженного обобщенного канонического корреляционного анализа (SGCCA) демонстрирует значительное улучшение благодаря применению фреймворка SLEP/SLBB. Данный подход позволяет выявлять существенные взаимосвязи в данных высокой размерности, эффективно отсеивая шум и незначимые факторы. Использование SLEP/SLBB обеспечивает не только повышение точности идентификации истинных корреляций, но и улучшает интерпретируемость полученных результатов, представляя их в более компактной и понятной форме. В ситуациях, когда количество переменных значительно превышает количество наблюдений, SGCCA с фреймворком SLEP/SLBB предоставляет мощный инструмент для извлечения значимой информации и построения эффективных моделей.

Метод разреженного канонического корреляционного анализа (SGCCA) активно использует ограничение разреженности, применяя $l_{2,1}$ -норму для получения экономных решений. Это не только упрощает интерпретацию результатов, выделяя наиболее значимые связи между переменными, но и существенно снижает вычислительные затраты. Вместо анализа всех возможных комбинаций, SGCCA фокусируется на небольшом подмножестве, что особенно важно при работе с данными высокой размерности. Такой подход позволяет выявлять ключевые факторы, влияющие на взаимосвязь между наборами переменных, делая анализ более эффективным и понятным для исследователя.

Полученные результаты демонстрируют, что разработанный алгоритм, основанный на методе SLEP/SLBB, обеспечивает сопоставимую скорость сходимости с более сложными римановыми методами при решении задач канонической корреляции. В частности, достигнутые значения целевой функции и нарушения условий Каруша-Куна-Таккера (ККТ) составляют порядка 10^-5, что свидетельствует о высокой точности решения. При этом, в отличие от римановых методов, требующих значительных вычислительных ресурсов, предложенный подход значительно снижает вычислительные затраты, делая его более эффективным и применимым для анализа больших объемов данных. Это достигается за счет использования специфической структуры разреженности, позволяющей упростить процесс оптимизации и уменьшить количество необходимых итераций.

Теоретические Гарантии и Перспективы Развития

Эффективность алгоритма SLBB в достижении оптимальных решений базируется на строгих математических основаниях, в частности, на неравенстве Лояшевича. Данное неравенство гарантирует, что функция ошибки, используемая в алгоритме, сходится к своему минимуму с определённой скоростью, даже в сложных, невыпуклых пространствах. $L(x_k) - L(x^<i>) \leq c ||x_k - x^</i>||^2$ , где $L(x)$ — функция ошибки, $x^*$ — оптимальное решение, а $c$ — положительная константа. Таким образом, математическая база алгоритма SLBB обеспечивает не только его работоспособность, но и предсказуемость поведения, что критически важно для задач оптимизации в машинном обучении и анализе данных.

Дальнейшие исследования сосредоточены на разработке адаптивных стратегий настройки параметра штрафа для повышения устойчивости и эффективности фреймворков SLEP/SLBB. Традиционные методы часто требуют ручной настройки данного параметра, что может быть трудоемким и приводить к субоптимальным результатам. Автоматическая адаптация параметра штрафа в процессе оптимизации позволит алгоритму динамически реагировать на характеристики решаемой задачи, ускоряя сходимость и улучшая качество получаемых решений. В частности, перспективным направлением является использование эвристических подходов или методов машинного обучения для определения оптимального значения параметра штрафа на каждой итерации, что потенциально может значительно расширить область применимости и повысить надежность указанных алгоритмов в различных сценариях оптимизации.

Предложенная методология, изначально разработанная для решения задач оптимизации с ограничениями, обладает значительным потенциалом для расширения сферы применения в различных областях машинного обучения и анализа данных. Успешное применение алгоритмов, основанных на подобных подходах, может привести к существенным улучшениям в задачах, требующих поиска оптимальных решений при соблюдении определенных условий, таких как обучение с регуляризацией, сжатие моделей, и построение рекомендательных систем. Более того, адаптация данной методики к новым типам ограничений и функциям потерь позволит решать более сложные и реалистичные задачи, открывая новые горизонты для инноваций в области искусственного интеллекта и обработки информации. Перспективным направлением представляется применение данной методологии к задачам, где ограничения описывают не только математические соотношения, но и бизнес-правила или требования к справедливости и этичности моделей.

Исследование представляет собой элегантное решение задачи оптимизации на обобщенных многообразиях Стифеля. Авторы демонстрируют, что предложенный ими метод локально точного штрафа (SLEP) эквивалентен исходной задаче, что подчеркивает важность структурного подхода к решению сложных проблем. Как отмечал Эрнест Резерфорд: «Если бы я не был физиком, я хотел бы быть философом». Эта фраза отражает глубокое понимание взаимосвязей между различными областями знания, подобно тому, как в данной работе взаимосвязь между структурой алгоритма и его эффективностью является ключевой. Метод SLEP, подобно хорошо спроектированной системе, проявляет свою эффективность благодаря четкой структуре и осознанию взаимосвязей между компонентами, что позволяет превзойти традиционные методы римановой оптимизации.

Что дальше?

Представленный метод, демонстрируя эквивалентность оптимизации на обобщённых многообразиях Стифеля исходной задаче, открывает новые горизонты, но и ставит вопросы. Элегантность решения часто скрывает сложность его адаптации к задачам, где структура многообразия далека от идеальной. Неизбежно возникает потребность в исследовании устойчивости метода к шуму и неточности данных — ведь в реальном мире редко встретишь идеальные условия. Особенно важно понять, как SLEP взаимодействует с задачами, где разреженность решения не является жёстким требованием, а лишь желательным свойством.

Попытки расширить применимость метода за рамки обобщённых многообразий Стифеля, возможно, потребуют переосмысления штрафных функций и условий сходимости. При этом, упрощение, неизбежное в процессе обобщения, всегда несёт свою цену. Важно помнить, что каждая изощрённость в алгоритме влечёт за собой риск увеличения вычислительных затрат и потери устойчивости. Будущие исследования должны сосредоточиться на поиске баланса между точностью, скоростью и робастностью.

Наконец, наблюдаемое превосходство над стандартными методами Римановой оптимизации — это лишь первый шаг. Необходимо углубить понимание причин этого превосходства и выявить классы задач, где SLEP демонстрирует наиболее заметные преимущества. Иначе, рискуем получить ещё один инструмент, хорошо работающий в лабораторных условиях, но бесполезный в реальных приложениях.

Оригинал статьи: https://arxiv.org/pdf/2602.05631.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-09 01:15