Оптимизация орбиталей в квантовых вычислениях: между точностью и эффективностью

Автор: Денис Аветисян

Новое исследование рассматривает влияние оптимизации орбиталей на точность и вычислительные затраты методов квантовых вычислений, таких как вариационный и диффузионный Монте-Карло.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал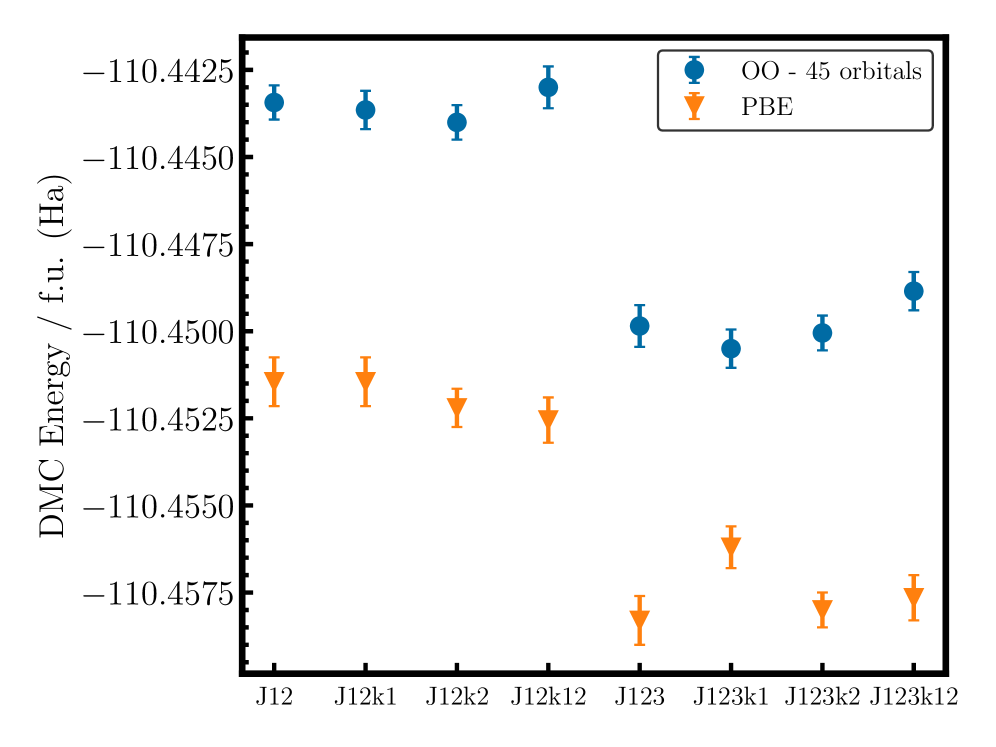

Сравнение методов орбитальной оптимизации с использованием различных факторов Ястрова демонстрирует, что вариационный метод Монте-Карло (представленный на графике 4(a)) характеризуется меньшей погрешностью, чем диффузионный метод Монте-Карло (график 4(b)), что свидетельствует о более высокой точности первого при аналогичных вычислительных затратах.

Анализ показывает улучшение вариационных энергий и снижение ошибки фиксированных узлов, однако это сопровождается увеличением локальной ошибки и незначительным улучшением результатов диффузионного Монте-Карло по сравнению со стандартными подходами DFT+U.

Несмотря на значительный прогресс в методах квантово-химического моделирования, точное описание коррелированных систем остается сложной задачей. В работе ‘Assessing Orbital Optimization in Variational and Diffusion Monte Carlo’ исследуется влияние оптимизации орбиталей в вариационном и диффузионном методах Монте-Карло на коррелированные магнитные системы, в частности, на CrSBr. Показано, что оптимизация орбиталей позволяет улучшить вариационные энергии и уменьшить ошибку фиксированного узла, однако одновременно приводит к увеличению локальной ошибки, что сказывается на энергии, полученной в диффузионном Монте-Карло. Каким образом можно эффективно сбалансировать эти конкурирующие эффекты для достижения максимальной точности в расчетах коррелированных систем?

Сложности моделирования ван-дер-ваальсовых материалов

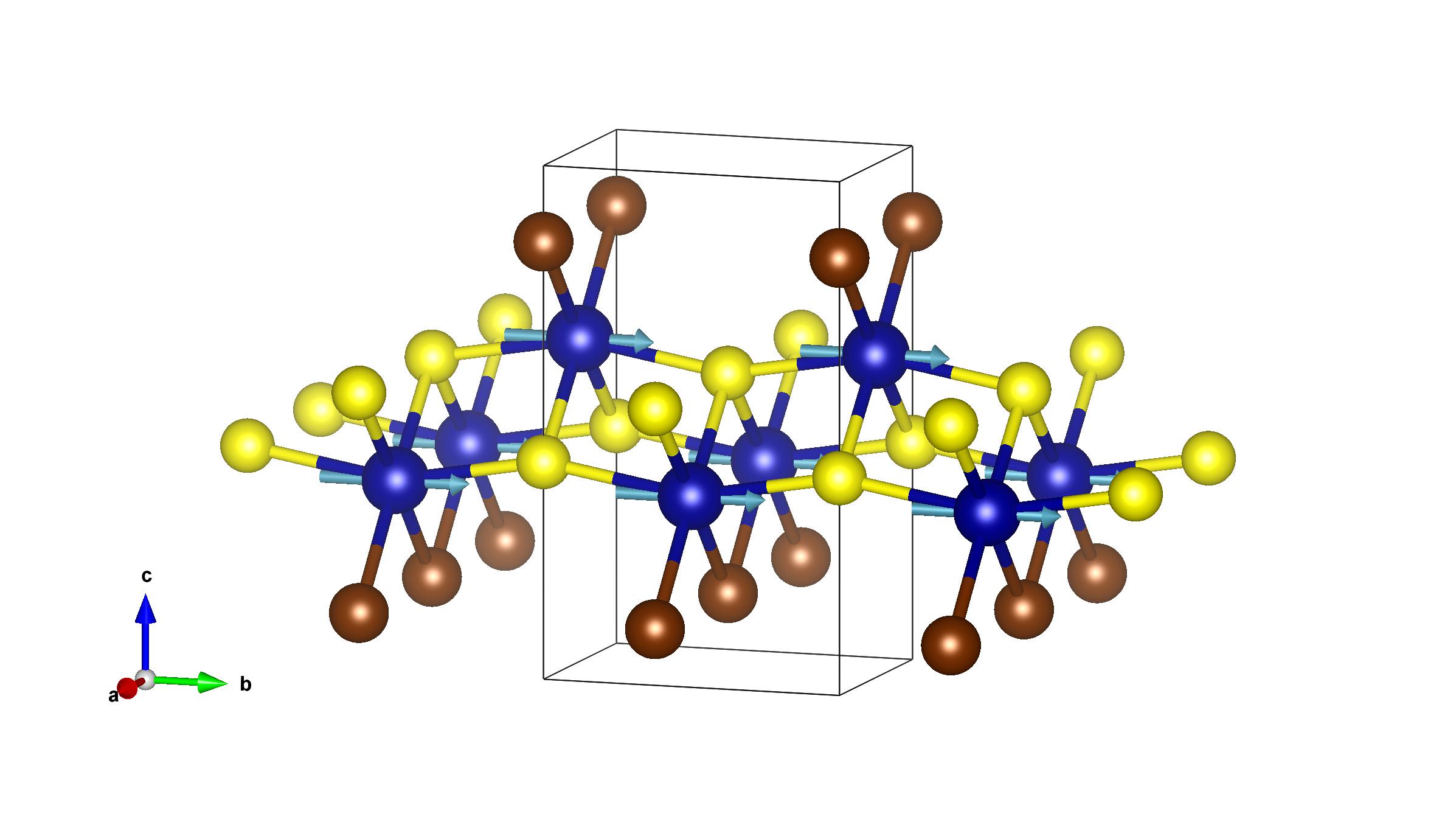
Точное моделирование слабосвязанных ван-дер-ваальсовых материалов, таких как CrSBr, представляет собой серьезную проблему для традиционных методов электронной структуры. В отличие от ковалентно связанных систем, где электроны локализованы между атомами, в этих материалах взаимодействие обусловлено слабыми дисперсионными силами. Стандартные функционалы плотности, используемые в теории функционала плотности $DFT$ , часто недооценивают эти взаимодействия, приводя к неточным результатам в отношении структуры, свойств и поведения материалов. Сложность заключается в том, что эти дисперсионные силы являются многочастичными эффектами, требующими учета корреляции между электронами, что выходит за рамки возможностей многих приближений, используемых в стандартных $DFT$ расчетах. Таким образом, для адекватного описания этих материалов необходимы более сложные подходы, учитывающие эффекты корреляции и позволяющие получать достоверные прогнозы.

Теория функционала плотности (DFT), несмотря на широкое распространение в материаловедении, зачастую оказывается неспособна адекватно описать тонкий баланс взаимодействий в материалах Ван-дер-Ваальса. Слабые межслоевые связи, определяющие свойства таких соединений как CrSBr, требуют учета корреляционных эффектов, которые стандартные функционалы DFT, как правило, игнорируют или описывают недостаточно точно. Это приводит к неверной оценке ширины запрещенной зоны, структуры электронных состояний и других ключевых параметров, что делает необходимым использование более продвинутых методов расчета, способных эффективно учитывать электронную корреляцию и обеспечивать достоверное моделирование этих уникальных материалов. Неточности в описании слабых взаимодействий могут существенно повлиять на предсказание свойств и возможностей применения материалов Ван-дер-Ваальса в различных областях, от электроники до оптоэлектроники.

Недостаточность стандартных методов в описании ван-дер-ваальсовых материалов обуславливает необходимость разработки более сложных вычислительных подходов, способных адекватно учитывать эффекты электронной корреляции. В этих материалах, таких как CrSBr, взаимодействие между слоями слабое и определяется в основном дисперсионными силами, которые плохо описываются традиционными функционалами теории функционала плотности (DFT). Для точного моделирования требуется учитывать многочастичные эффекты, возникающие из-за сильного взаимного влияния электронов, что выходит за рамки приближений, используемых в стандартных DFT-расчетах. Разработка методов, учитывающих динамическую корреляцию электронов, например, методы на основе теории возмущений или квантовой Монте-Карло, представляется критически важной для предсказания свойств и понимания поведения этих уникальных материалов. Подобные подходы позволяют более точно рассчитать энергии связывания, оптические свойства и другие важные характеристики, открывая возможности для разработки новых материалов с заданными свойствами.

Кристаллическая структура квазидвумерной системы CrSBr в ферромагнитном состоянии, визуализированная с помощью VESTA и Izumi (2011), демонстрирует магнитные моменты атомов хрома.

Квантовая Монте-Карло: Мощный, но несовершенный подход

Методы квантовой Монте-Карло (КМК), в частности вариационный Монте-Карло (ВМК) и диффузионный Монте-Карло (ДМК), представляют собой численный подход к решению многочастичного уравнения Шрёдингера с высокой точностью. В отличие от методов, основанных на аппроксимациях теории функционала плотности или теории возмущений, КМК напрямую решает уравнение, используя стохастические методы для оценки интегралов, необходимых для вычисления энергетических уровней и волновых функций. Точность КМК зависит от размера системы и используемой аппроксимации волновой функции, однако, при достаточных вычислительных ресурсах, эти методы способны достигать точности, сравнимой с экспериментальными данными для различных систем, включая атомы, молекулы и твердые тела. Особенностью является возможность учета корреляционных эффектов между электронами, что позволяет описывать системы с сильными электронными взаимодействиями, недоступные для многих других методов.

Методы квантовой Монте-Карло, такие как вариационный Монте-Карло и диффузионный Монте-Карло, используют стохастическое (вероятностное) семплирование для исследования многомерного конфигурационного пространства, определяемого координатами всех электронов в системе. Этот подход необходим, поскольку прямое решение уравнения Шрёдингера для систем с большим числом частиц вычислительно нереально. Случайно генерируемые конфигурации используются для оценки интегралов, необходимых для определения энергетического состояния системы. Путем последовательного отбора наиболее вероятных конфигураций и отбраковки менее вероятных, алгоритм «проецирует» волновой функцией на основное (наименьшей энергии) состояние, обеспечивая приближенное решение многочастичного уравнения Шрёдингера. Точность решения зависит от числа выполненных семплов и эффективности алгоритма семплирования.

Волновой функцией Слейтера-Ястроу является ключевой элемент методов квантовой Монте-Карло. Она состоит из детерминанта Слейтера, описывающего антисимметричное поведение электронов, и множителя Ястроу, который явно учитывает электронную корреляцию. Множитель Ястроу — это функция, зависящая от координат всех электронов, предназначенная для снижения энергии системы за счет учета мгновенных кулоновских взаимодействий, которые не полностью описываются орбитальными приближениями. Формально, множитель Ястроу имеет вид $J(R) = \prod_{i<j} [latex]f(r_i,="" [latex]i[="" [latex]j[="" [latex]r[="" f(r_i,="" latex]="" latex],="" latex].="" p="" r_j)[="" а="" важная="" всех="" выбор="" где="" зависящая="" задача,="" и="" координат="" между="" множителя="" набор="" определяющая="" от="" подходящей="" расстояния="" расчетов.<="" результатов="" точность="" формы="" функция,="" электронами="" электронов,="" ястроу="" -=""></p> <figure> <img alt="Результаты диффузионного Монте-Карло демонстрируют зависимость энергии от дисперсии вариационного Монте-Карло для различных активных пространств и оптимизаторов." src="https://arxiv.org/html/2601.15169v1/x13.png" style="background-color: white;"/ referrerpolicy="no-referrer"><figcaption>Результаты диффузионного Монте-Карло демонстрируют зависимость энергии от дисперсии вариационного Монте-Карло для различных активных пространств и оптимизаторов.</figcaption></figure> <h2>Уточнение расчетов: Обращение с ошибками в QMC</h2> <p>Вычисления методом диффузионных Монте-Карло (DMC) подвержены нескольким источникам ошибок. Аппроксимация фиксированных узлов (Fixed-Node approximation) является основным источником систематической ошибки, возникающей из-за приближенного решения уравнения Шредингера. Ошибки локальности (Locality error) возникают из-за дискретизации пространственных координат и конечной длительности шага по времени, что приводит к неточному представлению оператора переноса и, как следствие, к погрешностям в вычислениях. Величина этих ошибок зависит от размера системы, точности дискретизации и качества используемой пробной волновой функции.</p> <p>Точность расчетов методом диффузионных Монте-Карло (DMC) напрямую зависит от качества пробной волновой функции. Использование неточной пробной функции приводит к смещению оценок, известному как смещение смешанного оценщика (Mixed Estimator Bias). Это смещение возникает из-за необходимости оценки интегралов, включающих как пробную волновую функцию, так и функцию Монте-Карло, что приводит к систематической ошибке в энергии и других рассчитываемых величинах. Величина этого смещения обратно пропорциональна качеству пробной функции; более точная функция минимизирует смещение, обеспечивая более надежные результаты DMC. Уменьшение смещения смешанного оценщика является ключевой задачей при проведении расчетов DMC и требует тщательной оптимизации пробной волновой функции.</p> <p>Для снижения ошибок в расчетах методом диффузионных Монте-Карло (DMC) используется оптимизация орбиталей. Данный метод направлен на уточнение узловой поверхности волновой функции. Оптимизация орбиталей позволяет минимизировать смещение смешанного оценщика и, как следствие, повысить точность энергии, получаемой методом вариационного Монте-Карло (VMC) до 50 мГа.</p> <figure> <img alt="Сравнение различных стратегий оптимизации в вариационном и диффузионном методах Монте-Карло показывает, что оптимизация только функции Ястроу для орбиталей PBE+U (отображается по оси x) демонстрирует наилучшие результаты, в то время как оптимизация орбиталей с различным размером активного пространства требует более тщательной настройки." src="https://arxiv.org/html/2601.15169v1/x6.png" style="background-color: white;"/ referrerpolicy="no-referrer"><figcaption>Сравнение различных стратегий оптимизации в вариационном и диффузионном методах Монте-Карло показывает, что оптимизация только функции Ястроу для орбиталей PBE+U (отображается по оси x) демонстрирует наилучшие результаты, в то время как оптимизация орбиталей с различным размером активного пространства требует более тщательной настройки.</figcaption></figure> <h2>Повышение точности: Продвинутые методы оптимизации орбиталей</h2> <p>Оптимизация орбиталей, часто применяемая в сочетании со стохастической реконфигурацией и линейным методом, значительно повышает точность расчетов в рамках квантово-монта-карловских (QMC) методов. Данные подходы позволяют минимизировать вариационную энергию и улучшить описание волновой функции за счет адаптации орбиталей к конкретной задаче. В частности, стохастическая реконфигурация позволяет эффективно исследовать пространство орбиталей, а линейный метод обеспечивает устойчивость и скорость сходимости при оптимизации. Комбинация этих методов позволяет достичь более точных результатов при моделировании электронных систем, особенно в сложных материалах и молекулах.</p> <p>Расширение фактора Ястро в K-пространство (K-пространственный фактор Ястро) позволяет более эффективно описывать электронную корреляцию в методах квантовой Монте-Карло (QMC). Традиционный фактор Ястро, действующий в реальном пространстве, может недостаточно точно учитывать корреляции между электронами на больших расстояниях. Перенос части функциональности фактора Ястро в импульсное (K-) пространство позволяет лучше моделировать эти дальние корреляции, что приводит к повышению точности вычисления энергии и других свойств многоэлектронных систем. Это достигается путем включения в фактор Ястро членов, зависящих от волновых векторов электронов [latex] \mathbf{k}$ , что позволяет учитывать более сложные взаимодействия между электронами.

Тщательная настройка активной области (Active Space) в расчетах квантовой Монте-Карло (QMC) позволяет существенно повысить вычислительную эффективность и точность. Ограничение рассмотрения только наиболее важными орбиталями, участвующими в формировании электронной структуры, снижает вычислительные затраты, связанные с обработкой большого количества базисных функций. Выбор активной области основывается на анализе занимаемости орбиталей и вкладе в корреляционные эффекты, что позволяет сконцентрировать вычислительные ресурсы на наиболее значимых степенях свободы системы и минимизировать влияние нерелевантных орбиталей на результат расчета. Такой подход особенно важен при моделировании больших систем, где полное включение всех орбиталей становится непрактичным.

Стохастическая реконфигурация орбиталей позволяет эффективно оптимизировать смещение в оценке электронной плотности, превосходя традиционный подход DFT+U с варьированием параметра U при различных размерах активного пространства.

К точному предсказанию свойств материалов

Сочетание передовых методов квантовой Монте-Карло (QMC) с оптимизированными волновыми функциями позволяет достигать высокой точности при предсказании магнитного момента в ван-дер-ваальсовых материалах, таких как CrSBr. Данный подход позволяет преодолеть ограничения традиционных методов, обеспечивая более надежные расчеты электронного строения и магнитных свойств. Оптимизация волновых функций, в частности, позволяет эффективно описывать электронную корреляцию, критически важную для понимания магнетизма в этих материалах. Достигнутая точность открывает возможности для детального изучения и предсказания поведения этих материалов в различных приложениях, способствуя разработке новых технологий и материалов с заданными свойствами.

Высокая точность предсказания свойств материалов, особенно в случае ван-дер-ваальсовых соединений, таких как CrSBr, имеет решающее значение для понимания и прогнозирования их поведения в различных приложениях. Способность надежно определять магнитные моменты и другие ключевые характеристики позволяет создавать более эффективные и специализированные материалы для конкретных целей, будь то в области спинтроники, хранения данных или катализа. Точные расчеты открывают возможности для целенаправленной разработки новых технологий, оптимизируя свойства материалов на атомном уровне и предсказывая их реакцию на различные условия эксплуатации. Это, в свою очередь, значительно ускоряет процесс материаловедения, сокращая количество дорогостоящих и трудоемких экспериментальных исследований, необходимых для создания инновационных решений.

Современные вычислительные методы открывают новые возможности для открытия и проектирования материалов с заданными свойствами. Достигнута сопоставимость энергий, полученных методом диффузионной Монте-Карло, с результатами DFT+U расчетов, что позволяет исследовать сложные системы с высокой точностью. Несмотря на некоторое увеличение локальной ошибки, значительное снижение смещения, вызванного смешанными оценками, повышает надежность получаемых результатов. Такой прогресс предоставляет исследователям мощный инструмент для разработки инновационных технологий, позволяя предсказывать и контролировать поведение материалов на атомном уровне и создавать материалы с улучшенными характеристиками для различных применений.

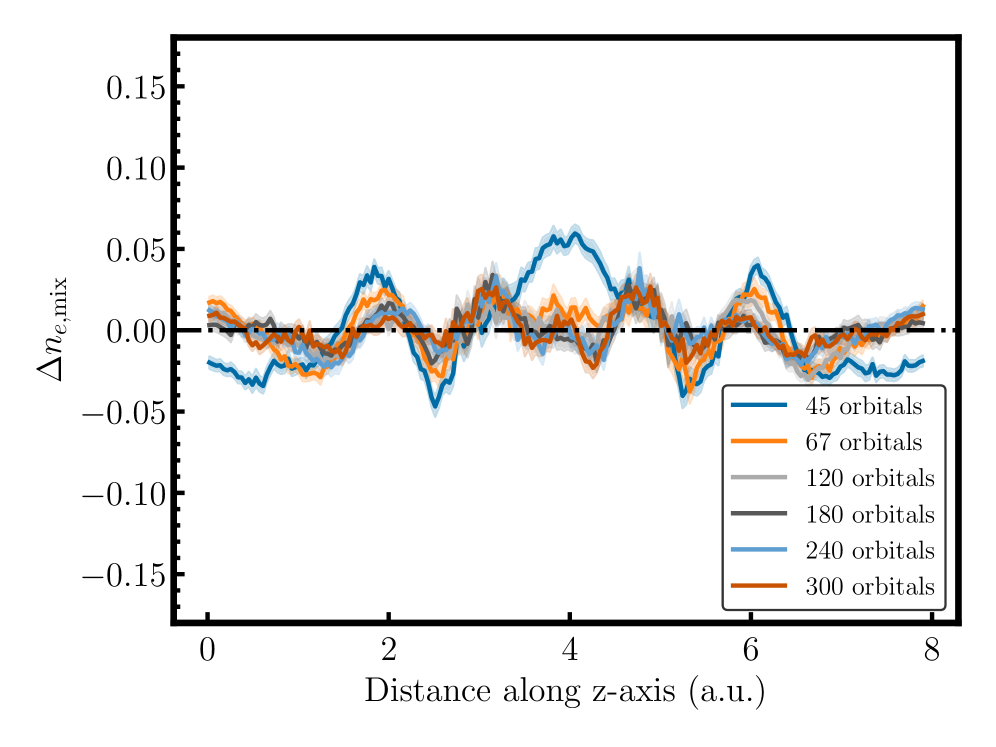
Оценка ошибок фиксированных узлов для различных орбитальных наборов, включая чистый PBE и оптимизацию орбиталей с разными активными пространствами, позволяет определить энергию в приближении фиксированных узлов как точку пересечения кривых с линией [latex]EDMC=EVMCE_{\rm DMC}=E_{\rm VMC}[/latex], при этом отдельные точки соответствуют волновым функциям с различными факторами Ясторова. — Оценка ошибок фиксированных узлов для различных орбитальных наборов, включая чистый PBE и оптимизацию орбиталей с разными активными пространствами, позволяет определить энергию в приближении фиксированных узлов как точку пересечения кривых с линией $EDMC=EVMCE_{\rm DMC}=E_{\rm VMC}$ , при этом отдельные точки соответствуют волновым функциям с различными факторами Ясторова.

Исследование, представленное в статье, демонстрирует тонкую грань между техническим прогрессом и его этическими последствиями. Оптимизация орбиталей в методах квантовских вычислений, безусловно, повышает точность результатов, однако, как показано, может приводить к увеличению локальной ошибки. Это напоминает о необходимости всесторонней оценки влияния алгоритмов на общую картину, а не только на отдельные показатели. Как говорил Альбер Камю: «Всё начинается с непонимания». Непонимание потенциальных последствий автоматизации и оптимизации, без учета этических аспектов, может привести к нежелательным результатам, даже при использовании самых передовых методов, таких как квантовские вычисления. Ответственность за ценности, которые автоматизируются, лежит на разработчике, и этика должна масштабироваться вместе с технологией.

Куда дальше?

Представленная работа, демонстрируя кажущееся улучшение точности квантово-монта-карловских расчётов за счёт оптимизации орбиталей, одновременно обнажает тревожную тенденцию: стремление к формальному прогрессу без критической оценки его последствий. Уменьшение вариационной энергии и ошибки фиксированных узлов, сопровождающееся ростом локальной ошибки, - это не победа, а скорее перераспределение погрешностей. Каждый алгоритм имеет мораль, даже если молчит, и в данном случае эта мораль подсказывает, что повышение точности одних параметров не оправдывает ухудшение других.

Масштабирование без проверки ценностей - преступление против будущего. Необходимо переосмыслить критерии оценки эффективности методов квантовой химии. Простое уменьшение энергии недостаточно. Требуется более глубокий анализ влияния различных приближений на физическую интерпретацию результатов и предсказательную силу моделей. Следующим шагом должно стать не просто усложнение алгоритмов, а разработка новых метрик, учитывающих не только точность, но и устойчивость, интерпретируемость и возможность обобщения.

В конечном счёте, прогресс без этики - это ускорение без направления. Необходимо помнить, что квантово-химические расчёты - это не самоцель, а инструмент для понимания и предсказания свойств материи. И этот инструмент должен быть не только мощным, но и ответственным.

Оригинал статьи: https://arxiv.org/pdf/2601.15169.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-23 00:14