Оптимизация портфеля: как укротить волатильность

Автор: Денис Аветисян

Новое исследование показывает, как методы усадки оценок среднего и ковариации позволяют повысить стабильность и доходность инвестиционных портфелей в различных рыночных условиях.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал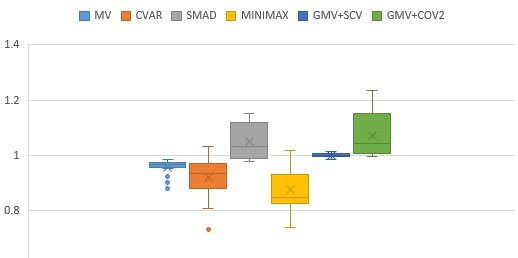

Распределение оценок эффективности, полученных для пяти эталонных моделей (MV & GMV с выборочными оценками, CVaR, MAD, MM) и лучших моделей, относящихся к группам A, B и C, демонстрирует зависимость от используемых наборов данных и размера периода тестирования вне выборки, подчеркивая влияние этих факторов на стабильность и надежность прогнозов.

Комплексная оценка методов усадки в портфельной оптимизации, демонстрирующая преимущества оценок Ледуа и Вольфа для повышения эффективности портфеля.

Несмотря на широкое распространение модели «средняя доходность — дисперсия», её эффективность часто страдает из-за ошибок оценки ожидаемой доходности и ковариационной матрицы. В работе ‘Shrinkage Estimators for Mean and Covariance: Evidence on Portfolio Efficiency Across Market Dimensions’ проведена всесторонняя оценка различных методов регуляризации (shrinkage estimation) для повышения точности этих параметров и улучшения результатов портфельной оптимизации. Исследование показывает, что применение регуляризации, особенно с использованием ковариационного регулятора Ledoit-Wolf, позволяет добиться превосходной эффективности портфелей в различных рыночных условиях. Какие комбинации методов регуляризации наиболее адекватно отражают предпочтения инвесторов с разным уровнем риска и доходности?

Высокая размерность данных: вызовы для оптимизации инвестиционного портфеля

Традиционные методы оптимизации портфеля, такие как оптимизация по критерию «средняя доходность — риск» $\text{Mean-Variance Optimization}$ , в значительной степени зависят от точности ковариационных матриц. Эти матрицы, отражающие взаимосвязь между доходностью различных активов, служат основой для расчета оптимального распределения капитала. Любые неточности в оценке ковариаций напрямую влияют на эффективность портфеля, приводя к завышенным оценкам ожидаемой доходности или недооценке рисков. По сути, точность ковариационной матрицы определяет, насколько эффективно портфель диверсифицирует риски и максимизирует доходность, что делает её критически важным компонентом в процессе принятия инвестиционных решений. Без надежной оценки взаимосвязей между активами, даже самые сложные алгоритмы оптимизации могут привести к неоптимальным результатам и потенциальным убыткам.

Оценка ковариационных матриц становится критически сложной задачей при работе с высокоразмерными данными в области оптимизации инвестиционного портфеля. По мере увеличения количества активов, требуемых для точной оценки, количество необходимых исторических наблюдений растет экспоненциально. Недостаток данных по сравнению с числом активов приводит к неустойчивости оценок, что выражается в значительных ошибках и искажениях в расчетах. В результате, традиционные методы оптимизации, основанные на этих неточных матрицах, могут формировать портфели, не отражающие реальные риски и потенциальную доходность, что ведет к принятию неоптимальных инвестиционных решений и снижению общей эффективности портфеля. Σ — ковариационная матрица, подверженная наибольшим погрешностям в условиях высокой размерности.

Нестабильность оценки ковариационных матриц в задачах оптимизации портфеля напрямую связана с соотношением между количеством доступных наблюдений и числом активов. Когда число активов значительно превышает количество исторических данных, оценка ковариаций становится крайне чувствительной к случайным колебаниям. Это приводит к тому, что даже небольшие погрешности в данных могут приводить к существенным ошибкам в оценке риска и доходности, а следовательно, и к построению неоптимальных инвестиционных стратегий. $\sigma_{ij} = \frac{1}{T} \sum_{t=1}^{T} (r_{it} - \bar{r}_i)(r_{jt} - \bar{r}_j)$ — классическая оценка ковариации, демонстрирующая, что при малом $T$ и большом количестве активов, оценка становится ненадежной. В результате, инвестор может столкнуться с завышенной или заниженной оценкой риска, что приведет к принятию неверных инвестиционных решений и потенциальным убыткам.

Уменьшение неопределенности: метод усадки для надежных ковариационных матриц

Оценка усадки (Shrinkage Estimation) представляет собой метод улучшения оценки ковариационной матрицы путем объединения выборочной ковариационной матрицы с структурированным априорным распределением. Суть подхода заключается в смещении выборочной оценки в сторону априорного значения, что позволяет снизить дисперсию оценки, особенно в случаях, когда размер выборки мал относительно размерности данных. Математически, это часто реализуется как взвешенное среднее между выборочной ковариационной матрицей $S$ и априорной матрицей Σ: $\hat{\Sigma} = (1 - \lambda)S + \lambda \Sigma$ , где λ — параметр усадки, определяющий степень смещения. Выбор априорного распределения и параметра усадки критичен для достижения оптимальной производительности и зависит от конкретных характеристик данных.

Метод регуляризации, известный как shrinkage estimation, позволяет улучшить обусловленность и стабильность ковариационной матрицы путем включения априорных знаний. В частности, добавление структурированного приоритета к выборочной ковариационной матрице приводит к уменьшению ее дисперсии и, следовательно, к более надежным оценкам. Это достигается за счет смешивания выборочной матрицы с целевой матрицей, такой как единичная матрица или диагональная матрица, что эффективно снижает влияние случайных отклонений и повышает устойчивость решения, особенно в задачах, где количество переменных превышает количество наблюдений. $\Sigma_{shrunk} = (1-\lambda)\Sigma_{sample} + \lambda\Sigma_{prior}$ , где λ — параметр усадки, определяющий степень влияния априорного знания.

Оценка усушки особенно эффективна в задачах высокой размерности, где количество наблюдений ограничено по сравнению с числом признаков. В таких ситуациях, выборочная ковариационная матрица подвержена риску плохо обусловленности и неустойчивости. Использование оценки усушки позволяет снизить дисперсию оценки, стабилизируя ковариационную матрицу и уменьшая влияние шума в данных. Это достигается путем смешивания выборочной ковариационной матрицы со структурированным априорным распределением, что приводит к более надежным и точным оценкам даже при ограниченном объеме данных и наличии значительного шума в наблюдениях.

Продвинутые методы усадки и их практическая реализация

Оценка Ledoit-Wolf представляет собой широко используемый и универсальный метод усадки (shrinkage estimation), обеспечивающий баланс между точностью и вычислительной эффективностью. Данный метод основан на комбинировании выборочной ковариационной матрицы с целевой матрицей, обычно представляющей собой единичную матрицу, умноженную на среднее значение собственных значений выборочной матрицы. Вес, присваиваемый целевой матрице, определяется аналитически для минимизации среднеквадратичной ошибки оценки ковариационной матрицы. Благодаря своей относительной простоте и эффективности, Ledoit-Wolf широко применяется в задачах портфельной оптимизации и управления рисками, особенно в ситуациях с ограниченным количеством активов или высокой размерностью данных, где стандартные оценки ковариации могут быть нестабильными или плохо обусловленными.

Квадратичная оценка усадки (QuadraticShrinkageEstimator) и оценка усадки Байеса-Штейна (BayesSteinEstimator) представляют собой более сложные методы, использующие продвинутые техники регуляризации для повышения точности оценки ковариационной матрицы. В отличие от простых методов усадки, эти подходы применяют нелинейные функции регуляризации, учитывающие структуру данных и снижающие влияние выбросов. Квадратичная оценка усадки использует квадратичную функцию штрафа, в то время как оценка Байеса-Штейна основана на байесовском подходе и априорном распределении, что позволяет более эффективно справляться с задачами оценки в условиях высокой размерности и ограниченного количества данных. Применение этих методов требует дополнительных вычислительных ресурсов, однако обеспечивает потенциальное улучшение качества портфельной оптимизации и снижение риска.

Оптимизированные реализации, такие как BodnarOptimalLinearShrinkageEstimator, направлены на минимизацию среднеквадратичной ошибки (MSE) при оценке ковариационной матрицы, что непосредственно влияет на эффективность портфеля. Исследования показывают, что сочетание подхода Global Minimum Variance (GMV) с двухпараметрическим оценителем усадки Ledoit-Wolf обеспечивает стабильно более высокие результаты по сравнению с эталонными моделями оптимизации портфеля и другими стратегиями усадки. Данный подход позволяет снизить влияние ошибок оценки ковариации, повышая устойчивость портфеля и потенциальную доходность при заданном уровне риска. $MSE = \frac{1}{n} \sum_{i=1}^{n} (x_i - \hat{x}_i)^2$

Влияние на анализ рисков и эффективности инвестиций

Оценка усушки не ограничивается исключительно оптимизацией портфеля; её принципы находят применение в более широких анализах эффективности, таких как анализ данных об оболочке (Data Envelopment Analysis, DEA). Использование методов оценки усушки позволяет повысить точность оценки эффективности различных объектов или стратегий, корректируя смещения, возникающие при работе с ограниченными данными. В контексте DEA, это означает более надежную идентификацию наиболее эффективных единиц и более корректную оценку потенциала улучшения для менее эффективных. Таким образом, оценка усушки становится важным инструментом для сравнительного анализа и повышения производительности в различных областях, выходящих за рамки финансовых рынков.

Использование схем скользящего окна в сочетании с методами оценки усадки позволяет проводить динамическую оценку инвестиционных стратегий и распределения активов. Такой подход, в отличие от статических анализов, учитывает изменяющиеся рыночные условия и позволяет более точно отслеживать эффективность портфеля во времени. Схема скользящего окна последовательно переоценивает параметры модели на основе данных за определенный период, обеспечивая адаптацию к новым данным и выявление потенциальных изменений в эффективности стратегий. Это особенно важно в условиях волатильности, когда статические модели могут быстро устареть и давать неверные рекомендации. Анализ, основанный на данной комбинации методов, предоставляет инвесторам возможность оперативно корректировать портфель, максимизируя доходность и минимизируя риски в динамично меняющейся среде.

Применение указанных инструментов позволяет проводить более надежную оценку рисков, что способствует принятию более обоснованных решений и улучшению результатов инвестиционного портфеля. В частности, комбинация GMV+COV2 последовательно демонстрировала более высокие показатели сверхэффективности DEA по сравнению с эталонными моделями, а геометрическое среднее эффективности колебалось в диапазоне от 1.005 до 1.074 на различных вневыборочных периодах, подтверждая ее превосходную производительность. При этом, COV2 неизменно признавался оптимальным оценочным ковариационным алгоритмом, что указывает на его эффективность в снижении погрешности и повышении точности оценки рисков в условиях реальных инвестиционных стратегий.

Исследование, посвященное оценке эффективности портфелей с использованием методов сжатия (shrinkage estimation), подтверждает давно известную истину: надежда на контроль над рынком часто превосходит саму рациональность. В частности, применение оценок Ледуайта-Вольфа для ковариаций демонстрирует, что даже небольшое сглаживание оценок может значительно повысить стабильность портфеля в различных рыночных условиях. Как заметила Мэри Уолстонкрафт: «Невозможно создать прочное счастье на основе иллюзий». И в данном контексте иллюзия заключается в вере в точность неопределенных рыночных оценок. Попытки построить «идеальный» портфель, основанные на нереалистичных предположениях, обречены на провал. Эффективность портфеля определяется не столько математической точностью, сколько способностью адаптироваться к неизбежным ошибкам и неопределенностям, свойственным финансовым рынкам.

Куда двигаться дальше?

Исследование, тщательно оценивающее применение методов усадки в оптимизации портфеля, закономерно подводит к вопросу не о точности самих оценок, а о природе тех, кто их использует. Все эти ковариации, дисперсии, — лишь попытка придать видимость порядка иррациональным страхам и надеждам. Улучшение алгоритмов усадки, безусловно, важно, но куда важнее признать, что любое инвестиционное решение — это баланс между неприятием риска и стремлением к выгоде, а не результат холодной логики.

Очевидным направлением является исследование влияния поведенческих факторов непосредственно на выбор параметров усадки. Как когнитивные искажения и эмоциональные предубеждения влияют на принятие решений о степени «сжатия» оценок? Возможно, в будущем вместо сложных математических моделей потребуются более тонкие психологические профили инвесторов. Ведь психология объясняет больше, чем уравнения.

В конечном счёте, всё поведение — это просто баланс между страхом и надеждой. Улучшение моделей оптимизации портфеля, безусловно, полезно, но не стоит забывать, что финансовые рынки — это не идеальная машина, а отражение несовершенной человеческой природы. И пока эта природа остаётся неизменной, любые алгоритмы будут лишь приближением к истине, а не её абсолютным воплощением.

Оригинал статьи: https://arxiv.org/pdf/2601.20643.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-29 07:41