Оптимизация с адаптацией: Новый подход к решению сложных задач

Автор: Денис Аветисян

В статье представлен усовершенствованный метод решения задач наименьших квадратов, сочетающий адаптивные алгоритмы и проекционные подходы для повышения скорости и устойчивости.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

На основе анализа данных MNIST, методы REBK, cRABEBK и aRABEBK демонстрируют возможности восстановления изображений при разреженных задачах наименьших квадратов, предлагая различные подходы к реконструкции исходных данных.

Разработан адаптивный рандомизированный расширенный метод Брегмана-Качмара (aRABEBK) для комбинированных задач оптимизации, демонстрирующий улучшенные скорости сходимости и устойчивость благодаря динамически настраиваемым параметрам релаксации.

Проблемы комбинированной оптимизации, включающие одновременно точность данных и регуляризацию, часто требуют значительных вычислительных ресурсов и тонкой настройки параметров. В данной работе представлена адаптивная рандомизированная блочная расширенная схема Качмара-Брегмана (aRABEBK), разработанная для эффективного решения подобных задач, как описано в статье ‘Adaptive Randomized Extended Bregman-Kaczmarz Method for Combined Optimization Problems’. Предложенный метод использует итеративно настраиваемые параметры релаксации, основанные на информации об остатке, что обеспечивает более быструю сходимость и повышенную устойчивость. Может ли данная схема стать основой для разработки новых алгоритмов, способных решать сложные задачи восстановления данных и машинного обучения с минимальными затратами вычислительных ресурсов?

Основы: Метод наименьших квадратов и алгоритм Качмараза

Проблема наименьших квадратов является фундаментальным элементом современной обработки данных, стремящимся к нахождению оптимального приближения к наблюдаемым данным. В основе этой концепции лежит минимизация суммы квадратов разностей между наблюдаемыми и предсказанными значениями. $\min_{x} \sum_{i=1}^{n} (y_i - f(x_i))^2$ — эта простая, но мощная формула отражает суть метода, позволяя оценивать параметры моделей, находить наилучшие соответствия в регрессионных задачах и решать широкий спектр задач оптимизации. От анализа данных в экономике до обработки изображений и машинного обучения, проблема наименьших квадратов предоставляет надежный и широко применяемый инструмент для извлечения полезной информации из данных и построения точных предсказаний.

Традиционные методы решения систем линейных уравнений, такие как прямое исключение Гаусса, часто сталкиваются с серьезными трудностями при работе с задачами большого масштаба или при наличии несовместности системы. В подобных случаях вычислительная сложность и потребность в памяти резко возрастают, а прямое вычисление решения становится невозможным или непрактичным. Вместо этого, исследователи обращаются к итеративным алгоритмам, которые постепенно приближаются к решению, обновляя его на каждой итерации. Эти методы, хотя и требуют больше вычислительных шагов, позволяют эффективно работать с огромными объемами данных и находить приближенные решения даже в случае несовместности, когда точного решения не существует. Использование итеративных подходов становится особенно важным в современных областях, таких как машинное обучение и обработка больших данных, где размер систем уравнений может достигать миллионов или даже миллиардов переменных.

Алгоритм Качмараза представляет собой итеративный метод решения систем линейных уравнений, основанный на последовательной проекции на гиперплоскости, определяемые отдельными ограничениями системы. Вместо прямого вычисления решения, алгоритм постепенно приближается к нему, выполняя проекции вектора решения на каждую гиперплоскость, соответствующую уравнению в системе. Каждая проекция уменьшает ошибку, пока не будет достигнуто достаточно точное приближение. Этот подход особенно эффективен для больших и разреженных систем, где традиционные методы могут быть вычислительно затратными или непрактичными. В отличие от методов, требующих одновременного решения всей системы, алгоритм Качмараза обрабатывает уравнения последовательно, что позволяет ему эффективно использовать память и распараллеливаться. Эффективность алгоритма зависит от порядка, в котором обрабатываются уравнения, и от свойств самой системы уравнений.

Анализ относительной ошибки в зависимости от числа итераций показывает, что для переопределенных и недоопределенных гауссовых матриц достигается минимально-нормальное наименьших квадратов решение.

Преодоление ограничений: расширения и рандомизация

Метод Расширенного Качмараза (Extended Kaczmarz Method) предназначен для решения переопределенных систем уравнений, не имеющих точного решения. В отличие от классического метода Качмараза, он вводит вспомогательные переменные, позволяющие находить приближенные решения в случае несовместимости системы. Это достигается путем преобразования исходной системы в систему с дополнительными степенями свободы, что позволяет алгоритму сходиться к минимально возможному отклонению от заданных ограничений, даже если точное удовлетворение всех уравнений невозможно. Введение вспомогательных переменных эффективно смягчает влияние несовместимости и обеспечивает сходимость алгоритма к некоторому допустимому решению.

Рандомизация в методе Качмараза направлена на ускорение сходимости и снижение вычислительных затрат. В стандартном методе Качмараза обновления производятся последовательно для каждой строки системы линейных уравнений. В рандомизированном варианте строки выбираются случайным образом для обновления на каждой итерации. Такой подход позволяет избежать последовательной обработки всех строк, особенно в случаях, когда система велика и разрежена. Выбор строк с использованием вероятностного распределения, пропорционального норме соответствующих строк, позволяет эффективнее приближаться к решению и снижает общую вычислительную сложность алгоритма. Это особенно важно для плохо обусловленных систем, где стандартный метод Качмараза может сходиться медленно или вовсе не сходиться.

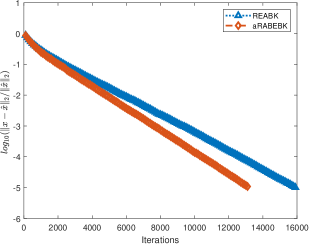
Метод Randomized Extended Kaczmarz (REK) представляет собой надежное и эффективное решение для плохо обусловленных или несовместных линейных систем. Однако, его производительность может быть улучшена. Метод adaptive randomized averaging block extended Bregman-Kaczmarz (aRABEBK) демонстрирует более высокую теоретическую скорость сходимости, равную $1 - \frac{\mu_f^2}{\beta_{max} \mathcal{I} \|A\|_F^2} \cdot \gamma(\hat{x})$ , по сравнению с REK. Данный показатель отражает превосходство aRABEBK в достижении решения с заданной точностью за меньшее количество итераций, особенно в сложных случаях, когда традиционные методы испытывают затруднения.

В условиях разреженных наименьших квадратов, относительная ошибка уменьшается с увеличением числа итераций как для переопределенных (верхний график), так и для недоопределенных (нижний график) построенных матриц.

Использование априорных знаний: брегмановские расстояния

Метод Брегмана-Качмара вводит понятие брегмановских расстояний, представляющих собой мощный инструмент для включения априорных структурных ограничений и регуляризации в процесс решения задач. В отличие от традиционных методов, использующих евклидово расстояние, брегмановские расстояния позволяют учитывать специфические свойства данных и целевой функции, что обеспечивает более эффективную и точную оптимизацию. Использование брегмановских расстояний позволяет формализовать априорные знания о структуре решения, например, требование разреженности или гладкости, и интегрировать их непосредственно в алгоритм, направляя итерационный процесс к более осмысленным и желаемым результатам. $d_f(x, y) = f(x) - f(y) - <\nabla f(y), x - y>$ — общая формула для брегмановского расстояния, где f — строго выпуклая функция.

Метод Брегмана-Качмара использует брегмановские расстояния для интеграции априорных структурных ограничений и регуляризации в процесс решения. В отличие от традиционных методов, использующих евклидово расстояние, брегмановские расстояния позволяют учитывать специфические свойства данных, направляя итерационный процесс к более осмысленным решениям. Это достигается за счет определения расстояния не только на основе разницы между значениями, но и с учетом структуры пространства данных, что особенно полезно при работе с разреженными данными или задачами, требующими минимальной нормы решения. Использование брегмановских расстояний позволяет алгоритму адаптироваться к характеристикам данных и находить решения, более соответствующие исходным условиям и требованиям.

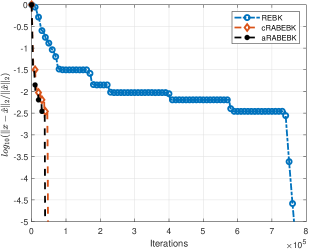
Метод aRABEBK позволяет эффективно решать задачи Sparse Least Squares (разреженные наименьшие квадраты) за счет включения ограничений разреженности. Теоретически доказана линейная скорость сходимости, выраженная формулой $1-μf2βmaxℐ‖A‖F2\cdot1σ~min2(A)\cdot|x^|min+2λ|x^|min$ . Практические тесты демонстрируют значительное снижение времени вычислений: aRABEBK выполняет задачу за 231.41 секунды, что в 12.7 раз быстрее, чем REBK (2941.99 секунды). В задачах восстановления изображений aRABEBK достигает PSNR 46.35, превосходя результаты других методов, показавших значения 13.25 и 22.59.

Методы REABK и aRABEK позволяют восстанавливать изображения MNIST в условиях минимальной среднеквадратичной ошибки, демонстрируя эффективность реконструкции исходных данных.

Представленная работа демонстрирует стремление к лаконичности и эффективности в решении сложных оптимизационных задач. Авторы предлагают адаптивный метод aRABEBK, направленный на достижение оптимального баланса между скоростью сходимости и устойчивостью. Этот подход, подобно тщательному удалению избыточных элементов из сложной системы, позволяет добиться большей ясности и элегантности решения. Как однажды заметил Лев Ландау: «В науке главное — не накопление фактов, а создание стройной и логичной картины мира». Именно к этому принципу и стремится исследование, предлагая не просто алгоритм, а инструмент для более глубокого понимания и решения задач наименьших квадратов, особенно в контексте разреженного восстановления.

Куда Далее?

Предложенный метод, хотя и демонстрирует улучшенные скорости сходимости, не является панацеей. Сложность оптимизационных задач часто скрывается в неявных ограничениях и структуре данных. Упор на адаптивные параметры расслабления — шаг в верном направлении, но истинное упрощение требует отказа от избыточности в самом алгоритме. Необходимо задаться вопросом: не является ли стремление к универсальности лишь усложнением, маскирующим недостаток фундаментального понимания?

Перспективным направлением представляется исследование возможности применения предложенного подхода к задачам, где структура данных принципиально неоднородна. Ограниченность текущего анализа — в основном сосредоточенность на задачах наименьших квадратов и разреженного восстановления. Расширение области применимости потребует не просто адаптации параметров, а переосмысления самой концепции “блочного усреднения” — возможно, в сторону более гранулярных или, напротив, более агрегированных стратегий.

В конечном счете, ценность любого алгоритма измеряется не его сложностью, а его способностью к самоочищению. Стремление к элегантности — не прихоть, а признак глубокого понимания. Следующим шагом должно стать не добавление новых параметров, а избавление от тех, что не служат ясной цели. Простота — не ограничение, а доказательство зрелости.

Оригинал статьи: https://arxiv.org/pdf/2601.11157.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-20 20:01