Оптимизация стратегий: новый взгляд на минимизацию остатков уравнения Беллмана

Автор: Денис Аветисян

В статье представлен углубленный анализ теоретических свойств и сходимости методов минимизации остатков уравнения Беллмана, применяемых для оптимизации стратегий в марковских процессах принятия решений.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

В процессе обучения значения [latex]Q_k(1,1)[/latex] и [latex]Q_k(1,2)[/latex] сходятся к оптимальным значениям [latex]Q_{\lambda}^{\<i>}(1,1)[/latex] и [latex]Q_{\lambda}^{\</i>}(1,2)[/latex] соответственно, демонстрируя сходимость алгоритма к оптимальной политике, при этом пунктирные линии указывают на соответствующие оптимальные Q-значения. — В процессе обучения значения $Q_k(1,1)$ и $Q_k(1,2)$ сходятся к оптимальным значениям $Q_{\lambda}^{\<i>}(1,1)$ и $Q_{\lambda}^{\</i>}(1,2)$ соответственно, демонстрируя сходимость алгоритма к оптимальной политике, при этом пунктирные линии указывают на соответствующие оптимальные Q-значения.

Исследование посвящено анализу сходимости стандартных и смягченных подходов минимизации остатков уравнения Беллмана с использованием градиентного спуска и субдифференциалов Кларка.

Несмотря на широкое распространение динамического программирования для решения задач Марковских процессов принятия решений, альтернативный подход, минимизация остатка уравнения Беллмана, остается недостаточно изученным. В работе ‘Analysis of Control Bellman Residual Minimization for Markov Decision Problem’ представлен анализ теоретических свойств и сходимости методов минимизации остатка уравнения Беллмана, включая стандартные и смягченные варианты, для оптимизации стратегий управления. Ключевым результатом является установление фундаментальных свойств, необходимых для применения и анализа данных методов, использующих, в частности, оператор мягкого уравнения Беллмана и градиентный спуск. Каковы перспективы использования минимизации остатка Беллмана в задачах обучения с подкреплением и других областях, требующих эффективной оптимизации стратегий управления?

Последовательное принятие решений и марковские модели: Основа адаптивных систем

Многие задачи, с которыми сталкиваются современные интеллектуальные системы, представляют собой последовательность принимаемых решений, где каждое действие влияет на последующие шаги и конечный результат. От управления роботом в сложной среде до разработки стратегий в играх и оптимизации финансовых портфелей — во всех этих сценариях требуется агент, способный оценивать текущую ситуацию, выбирать оптимальное действие и прогнозировать его последствия во времени. Такой подход, известный как последовательное принятие решений, позволяет эффективно решать задачи, требующие планирования и адаптации к изменяющимся условиям, поскольку учитывает не только непосредственную выгоду от действия, но и его долгосрочное влияние на достижение поставленной цели. Это принципиально отличает его от задач, где решения принимаются изолированно, без учета контекста и будущих последствий.

Марковская модель принятия решений (МПР) представляет собой формальный математический аппарат, позволяющий структурировать задачи, связанные с последовательным принятием решений. В основе МПР лежит описание системы через состояния, определяющие текущую ситуацию агента; действий, которые агент может предпринять; вознаграждения, получаемые за каждое действие в конкретном состоянии; и вероятностей перехода, отражающих, как действия влияют на изменение состояния системы. $P(s'|s,a)$ — вероятность перехода в состояние $s'$ из состояния $s$ при выполнении действия $a$ . Такое четкое определение элементов позволяет математически описывать и анализировать процессы принятия решений, что особенно важно в областях, требующих оптимизации стратегии в динамически меняющейся среде, например, в робототехнике, экономике и теории игр.

Традиционные методы решения задач Марковских процессов принятия решений (MDP), такие как динамическое программирование, хотя и гарантируют оптимальное решение, сталкиваются с существенными вычислительными трудностями при увеличении размерности пространства состояний. В частности, алгоритмы, требующие полного перебора всех возможных состояний и действий, демонстрируют экспоненциальный рост вычислительной сложности с увеличением числа состояний. Это делает их непрактичными для задач реального мира, где пространство состояний может быть огромным, например, в задачах робототехники или управления сложными системами. $O(n^k)$ — типичная оценка сложности, где $n$ — число состояний, а $k$ — горизонт планирования. В связи с этим, активно разрабатываются альтернативные подходы, такие как методы Монте-Карло и обучение с подкреплением, направленные на снижение вычислительной нагрузки за счет приближенных решений и выборочного исследования пространства состояний.

Минимизация остатков Беллмана: Поиск оптимальной ценности

Минимизация остатков Беллмана представляет собой метод поиска оптимальных функций ценности, направленный на сокращение разницы между оцененным и истинным значением. Этот подход формально выражается как минимизация $||V(s) - Q(s,a)||_1$ , где $V(s)$ — оценка функции ценности состояния $s$ , а $Q(s,a)$ — функция оптимального действия в состоянии $s$ . Суть метода заключается в итеративном улучшении оценки функции ценности до тех пор, пока разница между оценкой и истинным значением не станет пренебрежимо малой, что обеспечивает сходимость к оптимальному решению. Уменьшение остатков Беллмана напрямую влияет на точность оценки и, следовательно, на качество политики управления.

Метод минимизации остаточного значения Беллмана использует итеративное применение оператора Беллмана для последовательного уточнения функции ценности до достижения сходимости. Оператор Беллмана, по сути, выполняет операцию резервного копирования (backup), обновляя оценку ценности состояния на основе оптимальной ценности последующих состояний и немедленной награды. Данный итеративный процесс позволяет постепенно приближаться к оптимальной функции ценности, что, в свою очередь, обеспечивает надежную основу для оценки политики и, как следствие, для определения оптимальной стратегии поведения агента в заданной среде. $V(s) = \max_a [R(s,a) + \gamma \sum_{s'} P(s'|s,a)V(s')]$ .

Стандартная минимизация остаточного значения Беллмана подвержена влиянию ошибок аппроксимации функций, что может существенно снижать производительность в сложных средах. Данная чувствительность возникает из-за того, что при использовании функций для представления ценности состояния, погрешности в этих функциях накапливаются и усиливаются в процессе итераций. В сложных пространствах состояний и действий, даже небольшие ошибки аппроксимации могут привести к значительному отклонению от оптимальной ценности и, как следствие, к неоптимальной политике. Особенно это проявляется при использовании линейных или других ограниченных аппроксиматоров, где невозможно точно представить сложные зависимости между состояниями и ожидаемыми наградами. Для смягчения данной проблемы используются различные методы, включая регуляризацию, выбор более сложных аппроксиматоров или применение алгоритмов, устойчивых к ошибкам аппроксимации.

В отличие от расходящегося метода P-VI (красный), градиентный спуск на SCBR (синий) демонстрирует устойчивое снижение ошибки с каждой итерацией.

Контрольное остаточное Беллмана: Уточнение оптимизации политики

Контрольное остаточное Беллмана является расширением минимизации остатка Беллмана, включающим в себя непосредственную оптимизацию политики в процесс минимизации. В отличие от традиционной минимизации остатка Беллмана, которая фокусируется исключительно на улучшении оценки функции ценности, КОВБ одновременно оптимизирует и функцию ценности, и политику, используя градиентный спуск для поиска оптимальной политики, минимизирующей остаток. Это достигается путем включения члена, зависящего от градиента политики, в функцию потерь, что позволяет алгоритму напрямую влиять на политику во время минимизации остатка. Таким образом, КОВБ обеспечивает более эффективный процесс обучения, поскольку позволяет избежать расхождений между оценкой функции ценности и фактической политикой, что часто встречается в стандартных алгоритмах обучения с подкреплением.

Метод Control Bellman Residual (CBR) использует линейную аппроксимацию функции ценности $V(s)$ для снижения вычислительной сложности и повышения масштабируемости. Вместо хранения и обновления значений для каждого состояния, функция ценности представляется в виде линейной комбинации признаков состояния $\phi(s)$ , что позволяет оценить $V(s)$ для любого состояния с использованием весов θ. Это значительно уменьшает объем памяти, необходимый для представления функции ценности, и ускоряет процесс обучения, особенно в задачах с большим пространством состояний. Использование линейной аппроксимации позволяет применять эффективные алгоритмы оптимизации для поиска оптимальных весов θ, минимизирующих ошибку Bellman.

Метод Control Bellman Residual (CBR) обеспечивает более тесную связь между оценкой функции ценности и улучшением политики, что приводит к повышению эффективности обучения. Традиционные алгоритмы часто разделяют эти два процесса, что может привести к расхождениям и замедлить сходимость. CBR, напротив, интегрирует оптимизацию политики непосредственно в процесс минимизации остатка Беллмана, позволяя политике адаптироваться к уточняющейся оценке ценности. Это приводит к более стабильному и быстрому обучению, поскольку улучшения в оценке ценности немедленно отражаются в политике, и наоборот, что позволяет агенту более эффективно исследовать пространство состояний и находить оптимальную стратегию поведения.

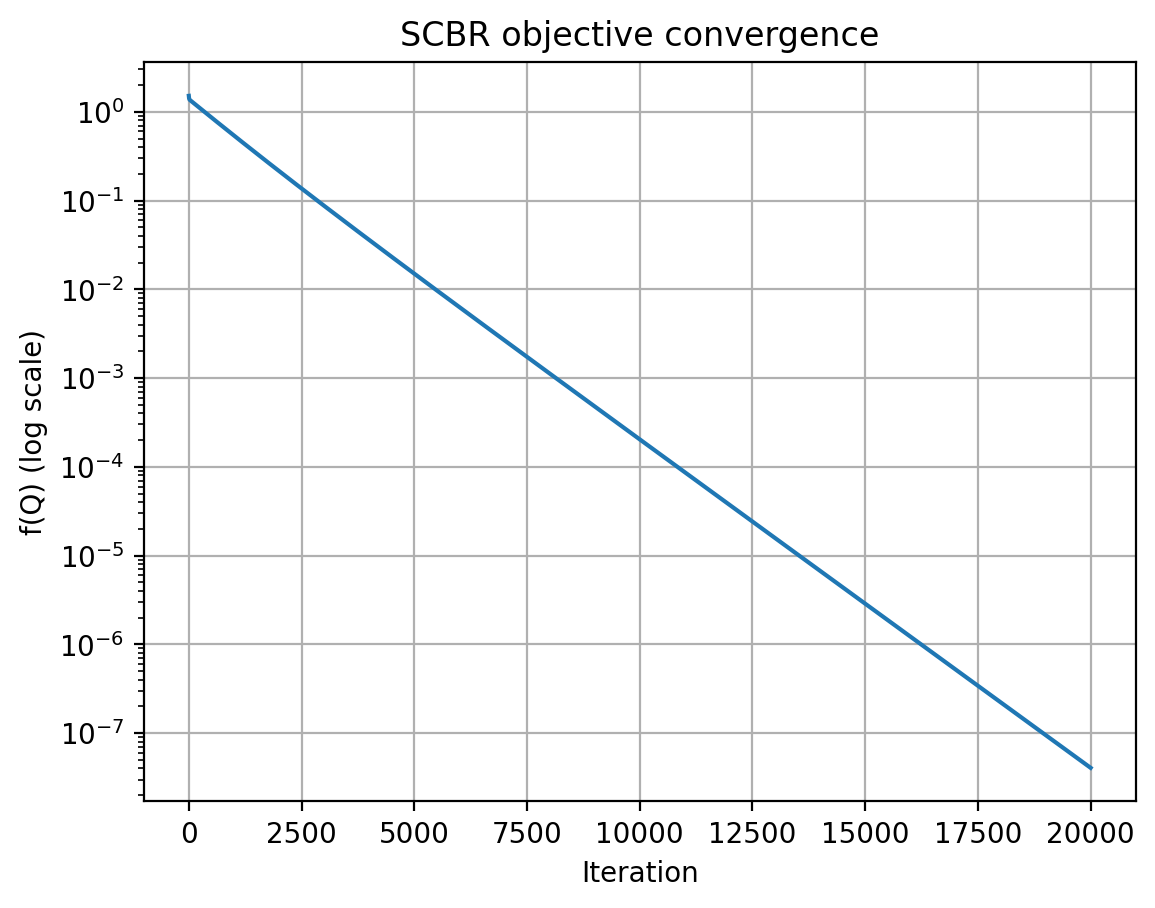
Значение целевой функции CBR, [latex]f(Q_k)[/latex], уменьшается в процессе применения метода субградиентного спуска для оптимизации [latex]Q_k[/latex]. — Значение целевой функции CBR, $f(Q_k)$ , уменьшается в процессе применения метода субградиентного спуска для оптимизации $Q_k$ .

Мягкое контрольное остаточное Беллмана: Дифференцируемый подход

Метод Soft Control Bellman Residual (SCBR) решает проблему недифференцируемости стандартного Control Bellman Residual (CBR) за счет использования “мягкого” оператора Беллмана. Традиционный CBR оперирует с функцией максимума, которая не имеет производной в точках, где несколько действий имеют одинаковое значение. SCBR заменяет эту операцию на взвешенную сумму, полученную с использованием $\text{Softmax}$ функции. Такой подход позволяет получить дифференцируемое приближение к оптимальному действию, что необходимо для применения методов градиентного спуска и других алгоритмов оптимизации, основанных на вычислении градиентов. В результате, SCBR обеспечивает возможность обучения политик управления в задачах, где стандартные методы, требующие дифференцируемости, неприменимы.

Метод Soft Control Bellman Residual (SCBR) эффективно обрабатывает недифференцируемые функции, используя концепции поддифференциала Кларка и ортогональной проекции. Поддифференциал Кларка позволяет обобщить понятие производной на недифференцируемые функции, предоставляя обобщенное понятие «направления» изменения. Ортогональная проекция, в свою очередь, используется для нахождения ближайшего решения в допустимом пространстве, что особенно важно при работе с ограничениями и негладкими функциями потерь. Комбинация этих двух инструментов позволяет SCBR находить стабильные и эффективные решения даже в случаях, когда традиционные методы оптимизации сталкиваются с трудностями из-за отсутствия производной или сложной структуры функции.

Использование оператора Softmax в Soft Control Bellman Residual (SCBR) позволяет применять градиентные методы оптимизации, такие как Gradient Descent, что обеспечивает более стабильное и эффективное обучение. В отличие от методов, требующих поиска шага методом обратного отслеживания (backtracking line search), SCBR демонстрирует экспоненциальную скорость сходимости при фиксированном размере шага. Это достигается благодаря сглаживанию оператора Беллмана, что позволяет вычислять градиенты даже для недифференцируемых функций, обеспечивая устойчивость и предсказуемость процесса обучения. $\lim_{n \to \in fty} ||x_n - x^<i>|| = 0$ , где $x_n$ — последовательность приближений, а $x^</i>$ — оптимальное решение.

Сравнительный анализ обучения с подкреплением на основе глубокого обучения (SCBR и DQN) в пяти задачах из среды Gymcontrol показал, что SCBR превосходит DQN в задачах [latex]CartPole-v1[/latex] и [latex]Acrobot-v1[/latex], но демонстрирует менее эффективные результаты в других сценариях. — Сравнительный анализ обучения с подкреплением на основе глубокого обучения (SCBR и DQN) в пяти задачах из среды Gymcontrol показал, что SCBR превосходит DQN в задачах $CartPole-v1$ и $Acrobot-v1$ , но демонстрирует менее эффективные результаты в других сценариях.

Математические основы и гарантии устойчивости

Сходимость алгоритма SCBR напрямую зависит от определенных математических свойств оптимизируемого пространства. В частности, ключевую роль играет условие Липшица непрерывности, гарантирующее ограниченность изменения функции отклика на изменения входных данных. Наличие стационарных точек, представляющих собой точки, в которых градиент функции равен нулю, также необходимо для обеспечения сходимости. Отсутствие таких точек или их неустойчивость может привести к осцилляциям и невозможности достижения оптимального решения. Таким образом, анализ оптимизационного ландшафта на предмет выполнения этих условий является важным этапом при применении SCBR, определяющим его эффективность и надежность.

Эффективность метода SCBR тесно связана с характеристиками квадратичных функций, используемых для аппроксимации. Анализ показывает, что оптимизационный процесс может приводить к множественным стационарным точкам, что означает существование нескольких возможных решений. Данное явление было продемонстрировано на примере простой задачи Марковского процесса принятия решений (MDP). Это указывает на то, что поиск оптимальной стратегии в сложных задачах может потребовать дополнительных механизмов для выбора наиболее подходящего решения из множества стационарных точек, а также учета особенностей используемой квадратичной аппроксимации, влияющих на форму оптимизационного ландшафта и стабильность алгоритма.

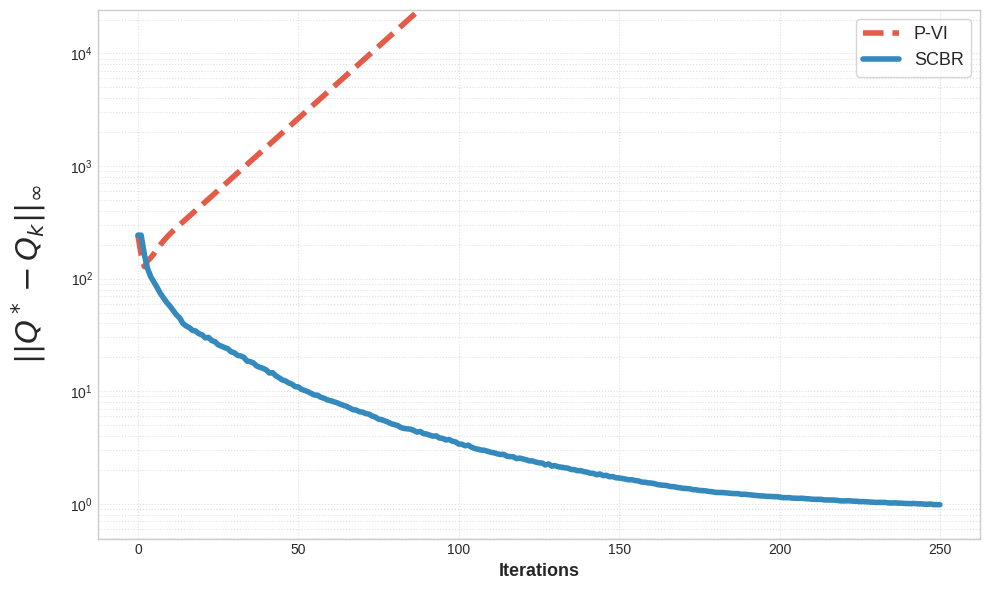
В среде FrozenLake-v1 разработанный алгоритм SCBR демонстрирует впечатляющий уровень успешности, достигающий 20.7%. Этот результат значительно превосходит показатели базового метода Projected Value Iteration (PVI), который в той же среде не смог добиться успеха ни в одном из случаев, показывая нулевой процент успешных решений. Полученные данные подтверждают эффективность SCBR в задачах, связанных с поиском оптимальной стратегии в детерминированных стохастических средах, и подчеркивают его потенциал в качестве альтернативы традиционным методам динамического программирования, особенно в случаях, когда стандартные алгоритмы оказываются неэффективными.

График демонстрирует уменьшение значения целевой функции SCBR в логарифмическом масштабе по мере выполнения итераций.

Исследование, представленное в данной работе, акцентирует внимание на минимизации остаточного уравнения Беллмана как методе оптимизации политик в марковских процессах принятия решений. Этот подход, стремящийся к сходимости и точности, напоминает о естественном ходе времени и старении систем. Тим Бернерс-Ли однажды заметил: «Web — это не просто набор технологий, это способ думать». Аналогично, минимизация остаточного уравнения Беллмана — это не просто технический метод, но и способ осмыслить и улучшить процессы принятия решений, адаптируясь к изменяющимся условиям и стремясь к оптимальному результату. Подобно тому, как системы стареют, методы оптимизации нуждаются в постоянной адаптации и совершенствовании, чтобы оставаться эффективными и релевантными.

Что же дальше?

Представленное исследование, тщательно изучившая сходимость методов минимизации остаточного уравнения Беллмана, лишь подтверждает старую истину: любая система, даже самая элегантная в своей математической конструкции, неизбежно стареет. Не ошибка порождает этот процесс, а сама неумолимость времени, проявляющаяся в накоплении неточностей и отклонений от идеала. Доказательства сходимости — это не гарантия вечной молодости алгоритма, а лишь констатация того, как долго он сможет сопротивляться энтропии.

Впрочем, кажущаяся стабильность, достигаемая посредством этих методов, может оказаться не более чем отсрочкой неизбежного. Насколько хорошо эти подходы масштабируются к реальным задачам, где пространство состояний бесконечно и шум непредсказуем? Игнорирование этих факторов — это подобно замазыванию трещин на фундаменте: конструкция может простоять еще какое-то время, но катастрофа лишь откладывается.

Будущие исследования, вероятно, должны сосредоточиться на разработке методов, способных адаптироваться к меняющимся условиям и справляться с неопределенностью, а не на бесконечной погоне за идеальной сходимостью. Необходимо признать, что любая модель — это лишь приближение к реальности, и задача состоит не в том, чтобы достичь абсолютной точности, а в том, чтобы создать систему, способную достойно стареть, извлекая уроки из ошибок и адаптируясь к неизбежным изменениям.

Оригинал статьи: https://arxiv.org/pdf/2601.18840.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-29 02:41