Оптимизация в реальном времени: новый подход к адаптивному обучению

Автор: Денис Аветисян

В статье представлен алгоритм, позволяющий эффективно обучать модели в условиях потоковых данных, минимизируя затраты на переключение и сохраняя высокую точность.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

В контексте оптимизации с использованием [latex] \ell_1 [/latex] и [latex] \ell_2 [/latex] норм, жадные алгоритмы стремятся к немедленному приближению к решению, проецируя текущую оценку [latex] y - g_t [/latex], в то время как ленивые алгоритмы учитывают предыдущую итерацию [latex] y - g_t - g_{t-1} [/latex], что демонстрирует разницу в подходе к минимизации и потенциальное влияние на скорость сходимости. — В контексте оптимизации с использованием $\ell_1$ и $\ell_2$ норм, жадные алгоритмы стремятся к немедленному приближению к решению, проецируя текущую оценку $y - g_t$ , в то время как ленивые алгоритмы учитывают предыдущую итерацию $y - g_t - g_{t-1}$ , что демонстрирует разницу в подходе к минимизации и потенциальное влияние на скорость сходимости.

Разработан алгоритм частично ленивого градиентного спуска (kk-lazyGD) для сглаженной онлайн-оптимизации выпуклых функций, обеспечивающий минимальный динамический риск и снижающий стоимость переключений.

Постоянный компромисс между быстрой реакцией на изменения и стабильностью обновлений представляет собой сложность в задачах онлайн-обучения. В данной работе, посвященной ‘Partially Lazy Gradient Descent for Smoothed Online Learning’, предложен алгоритм $k$ -lazyGD, позволяющий динамически балансировать между накоплением градиентов и адаптивностью. Доказано, что предложенный метод достигает оптимальной динамической сожаления $\mathcal{O}(\sqrt{(P_T+1)T})$ для любого уровня «ленивости» $k$ до $\Theta(\sqrt{T/P_T})$ , где $P_T$ — длина траектории компаратора. Может ли подобный подход к адаптивному накоплению градиентов стать основой для создания более устойчивых и эффективных алгоритмов онлайн-обучения в условиях меняющихся данных?

Онлайн-оптимизация: Вызов для инженера

Многие задачи машинного обучения могут быть сформулированы как сглаженная онлайн-оптимизация выпуклых функций (SOCO), что требует от алгоритмов способности адаптироваться к неизвестным и потенциально враждебным средам. В таких сценариях алгоритм последовательно принимает решения, получая обратную связь в виде градиента функции потерь, которая может меняться с каждым шагом. Это особенно актуально в приложениях, где данные поступают потоком, а оптимальная стратегия неизвестна заранее, например, в рекомендательных системах, финансовом моделировании или управлении роботами. Способность алгоритма эффективно учиться и адаптироваться к меняющимся условиям, минимизируя суммарные потери, является ключевым требованием для успешного решения задач SOCO, и именно это определяет сложность и актуальность исследований в данной области. $f(x,t)$ представляет собой функцию потерь, зависящую от действия $x$ и времени $t$ .

Традиционные методы онлайн-обучения, такие как непосредственное обновление градиентов, часто сталкиваются с серьезными трудностями, обусловленными зашумленностью градиентов и высокими вычислительными затратами. В условиях динамически меняющихся данных, градиенты, вычисленные на основе текущей информации, могут быть далеки от истинного направления спуска, что приводит к медленной сходимости или даже расходимости алгоритма. Более того, вычисление градиента на каждом шаге может быть чрезвычайно ресурсоемким, особенно для задач с высокой размерностью признаков или сложными моделями. Эта проблема усугубляется необходимостью обработки больших объемов данных в режиме реального времени, что требует разработки более эффективных и устойчивых к шуму алгоритмов для онлайн-оптимизации. Таким образом, поиск методов, позволяющих снизить вычислительную сложность и повысить устойчивость к зашумленным данным, является ключевой задачей в области онлайн-обучения.

Оценка эффективности алгоритмов онлайн-оптимизации требует пристального внимания к метрикам, таким как Динамическое Сожаление. Данная метрика позволяет количественно оценить, насколько уступает производительность алгоритма по сравнению с фиксированной, заранее заданной стратегией. Вместо сравнения с одним конкретным решением, Динамическое Сожаление измеряет кумулятивную разницу в потерях, учитывая, что оптимальная стратегия может меняться со временем. $Dynamic\ Regret = \sum_{t=1}^{T} (f(x_t) - f(x^<i>_t))$ , где $x_t$ — действие, выбранное алгоритмом на шаге t, а $x^</i>_t$ — оптимальное действие на этом шаге. Низкое значение Динамического Сожаления указывает на то, что алгоритм способен быстро адаптироваться к изменяющимся условиям и демонстрировать производительность, близкую к оптимальной, даже в неблагоприятных средах. Таким образом, эта метрика является ключевым инструментом для сравнения и анализа различных подходов к онлайн-оптимизации.

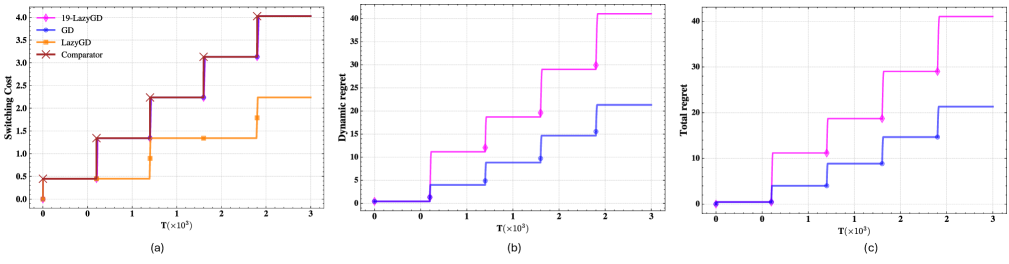
Анализ наихудшего случая для методов fork-lazyGD показывает, что каждая смена фазы является началом новой, при этом случайные или детерминированные выбросы отсутствуют, что подтверждается данными о стоимости переключения, динамическом сожалении и общем сожалении для GD, LazyGD и kk-LazyGD с различными значениями kk.

Ленивые обновления: Компромисс между скоростью и стабильностью

Механизм «ленивых» обновлений (Lazy Updates) предполагает накопление градиентов в течение нескольких шагов перед применением фактического действия. Это позволяет снизить вычислительную нагрузку, поскольку вычисление и применение обновлений происходит реже. Однако, накопление градиентов неизбежно приводит к увеличению «задержки» (staleness) — разницы между текущим состоянием градиентов и текущим состоянием среды, что может повлиять на скорость адаптации системы к изменениям. Эффективность данного подхода напрямую зависит от баланса между частотой применения обновлений и необходимостью минимизировать вычислительные затраты.

Одним из ключевых преимуществ «ленивых» обновлений является повышение стабильности системы. Накопление градиентов в течение времени позволяет сгладить случайные шумы в данных, прежде чем применить корректирующее действие. Этот процесс усреднения уменьшает влияние отдельных выбросов или кратковременных колебаний, что приводит к более плавному и предсказуемому поведению системы. Вместо немедленной реакции на каждый шумный сигнал, алгоритм интегрирует информацию за определенный период, формируя более надежную оценку направления обновления, что особенно важно в условиях нестабильной или зашумленной среды.

Управление степенью «ленивости» при использовании отложенных обновлений является критически важным аспектом, определяющим компромисс между вычислительной эффективностью и способностью системы реагировать на изменения внешней среды. Повышение степени отложенности (увеличение интервала между накоплением градиентов и применением действий) снижает вычислительную нагрузку, однако увеличивает риск использования устаревших данных для принятия решений. С другой стороны, снижение степени отложенности увеличивает частоту обновлений, повышая чувствительность к изменениям, но и требуя больше вычислительных ресурсов. Оптимальный баланс определяется спецификой решаемой задачи и доступными ресурсами, и требует тщательной настройки соответствующих параметров.

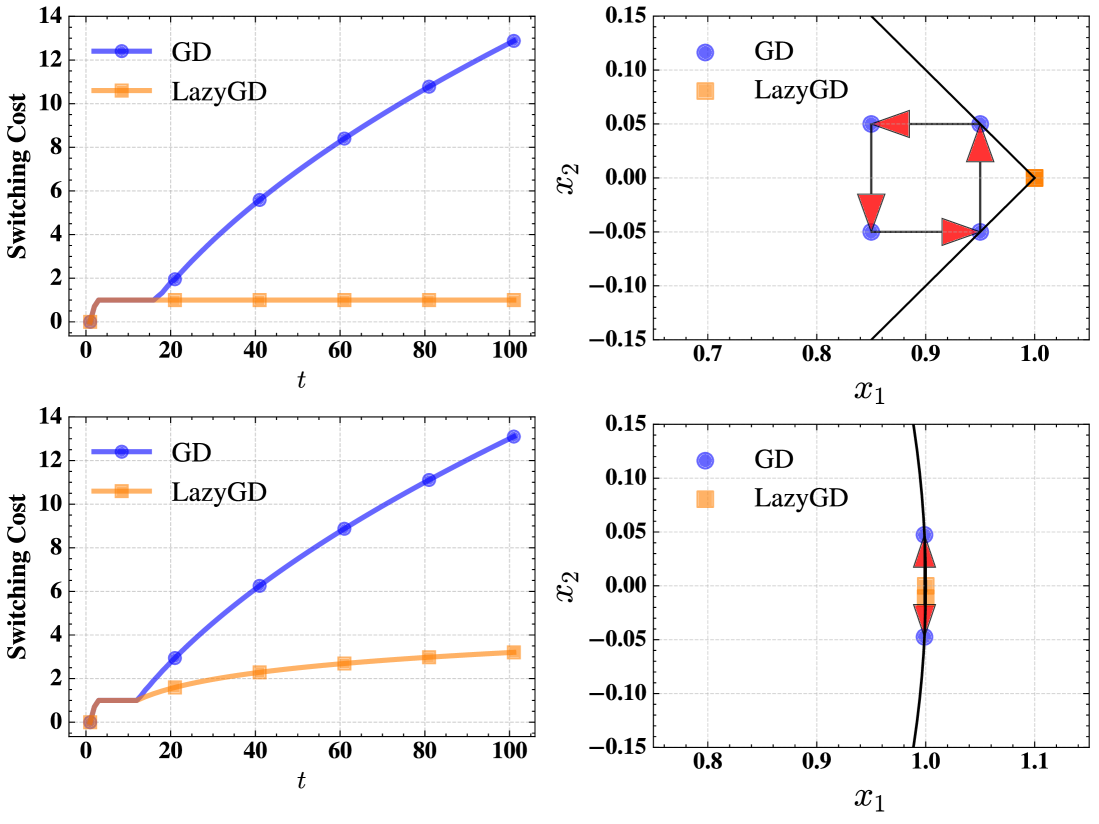
Сравнение стратегий обновления демонстрирует, что жадные обновления обеспечивают непрерывное движение, в то время как ленивые обновления остаются неизменными или перемещаются минимально, что проявляется в различиях стоимости переключения и динамике изменений в течение нескольких раундов.

KK-LazyGD: Гибкий подход к онлайн-обучению

Алгоритм KK-LazyGD решает проблему, присущую как жадным, так и полностью ленивым обновлениям, путем введения параметра ‘k’, определяющего степень «ленивости». При $k = 0$ алгоритм функционирует как полностью жадный, немедленно применяя каждое обновление. При $k = \infty$ он становится полностью ленивым, накапливая все градиенты и применяя их только в конце. В промежуточных значениях ‘k’ алгоритм представляет собой компромисс, применяя только часть накопленных градиентов на каждой итерации, что позволяет снизить вычислительные затраты по сравнению с жадными подходами и повысить стабильность по сравнению с полностью ленивыми.

Алгоритм KK-LazyGD использует фреймворк Follow-the-Regularized-Leader (FTRL), что позволяет эффективно управлять влиянием прошлых градиентов и поддерживать ограничения. В частности, применяется механизм отсечения (Pruning Mechanism), который уменьшает вклад устаревших градиентов, предотвращая их чрезмерное влияние на текущие обновления. Для обеспечения соблюдения ограничений на параметры модели используется евклидова проекция с использованием L2-нормы $||x||_2$ , которая гарантирует, что обновленные параметры остаются в допустимом диапазоне и предотвращает переобучение или нестабильность алгоритма. Такой подход позволяет алгоритму адаптироваться к изменяющимся данным и поддерживать оптимальную производительность.

Алгоритм KK-LazyGD достигает динамического сожаления порядка $O(\sqrt{T/PT})$ , соответствующего оптимальной скорости, за счет балансировки стоимости перемещения между экспертами и стоимости «попадания» (hitting cost) — штрафа за выбор неоптимального эксперта. Минимизация стоимости переключения (Switching Cost) дополнительно способствует снижению общего сожаления. Данный подход позволяет эффективно управлять компромиссом между исследованием (exploration) и использованием (exploitation) в условиях изменяющейся среды, обеспечивая гарантированную верхнюю границу на накопленное сожаление в течение времени $T$ , где $P$ представляет собой параметр, характеризующий частоту смены экспертов.

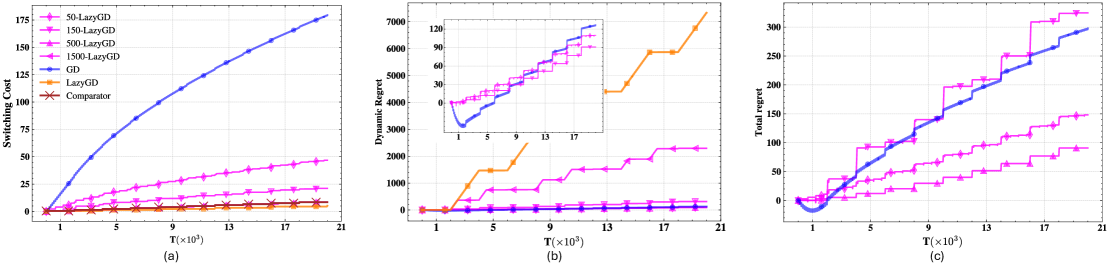
Сравнение алгоритмов GD, LazyGD и kk-LazyGD показывает, что увеличение значения kk приводит к снижению стоимости переключений, динамического сожаления и общего сожаления. — Сравнение алгоритмов GD, LazyGD и k-LazyGD показывает, что увеличение значения k приводит к снижению стоимости переключений, динамического сожаления и общего сожаления.

Эффективность и перспективы: Практическое применение алгоритма

Алгоритм KK-LazyGD демонстрирует высокую эффективность в задачах сглаженной онлайн-оптимизации (SOCO), достигая динамического сожаления порядка $O(\sqrt{T/PT})$ . Данный показатель указывает на способность алгоритма к адаптации и минимизации потерь при последовательном принятии решений в условиях неопределенности. В отличие от традиционных методов, KK-LazyGD эффективно справляется с задачами, где оптимальная стратегия со временем меняется, обеспечивая стабильно низкое сожаление даже при большом количестве итераций (T) и растущей размерности пространства признаков (P). Это делает его ценным инструментом для приложений, требующих быстрой адаптации к изменяющимся условиям и эффективного использования вычислительных ресурсов.

Алгоритм KK-LazyGD демонстрирует значительную приспособляемость к динамически меняющимся условиям, что делает его особенно ценным в задачах адаптивного обучения. Его способность эффективно функционировать в средах, где оптимальные стратегии со временем меняются, обусловлена механизмом «ленивых» обновлений. Вместо того, чтобы немедленно реагировать на каждый новый сигнал, KK-LazyGD оценивает целесообразность обновления, основываясь на балансе между минимизацией сожаления и затратами на переключение, что позволяет избегать ненужных вычислений и повышать устойчивость к шумам. Это делает его перспективным инструментом для широкого спектра приложений, включая финансовое моделирование, управление ресурсами и разработку систем искусственного интеллекта, где способность быстро адаптироваться к меняющимся обстоятельствам является ключевым фактором успеха. $O(\sqrt{T/PT})$ — динамическое сожаление алгоритма подчеркивает его эффективность даже в сложных и нестабильных условиях.

Алгоритм KK-LazyGD демонстрирует оптимальный баланс между минимизацией сожаления и снижением стоимости переключений благодаря параметру «ленивости» (k), равного $Θ(\sqrt(T/PT))$ . Данный параметр позволяет алгоритму эффективно адаптироваться к изменяющимся условиям, избегая частых и излишних переключений между моделями, что существенно снижает вычислительные затраты. В отличие от традиционных методов, которые часто сталкиваются с дилеммой между скоростью обучения и стабильностью, KK-LazyGD обеспечивает значительное улучшение производительности, позволяя достичь оптимального компромисса и более эффективно решать задачи гладкой онлайн-оптимизации. Это особенно важно в динамичных средах, где требуется адаптивное обучение и минимизация долгосрочных потерь.

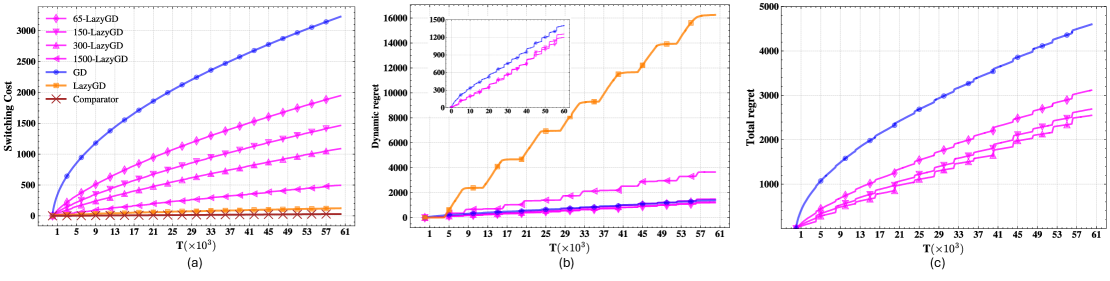
Сравнение алгоритмов GD, LazyGD и k-LazyGD показывает, что увеличение значения k приводит к снижению стоимости переключений, стоимости достижения цели и общего сожаления.

Исследование демонстрирует, что даже в области оптимизации, где стремятся к элегантным решениям, неизбежно возникает компромисс между точностью и вычислительными затратами. Алгоритм kk-lazyGD, предложенный в статье, иллюстрирует это: накопление градиентов, призванное снизить переключение между обновлениями, в конечном итоге требует балансировки с необходимостью быстрой реакции на изменения. Как метко заметил Джон фон Нейман: «В науке нет абсолютно ничего важнее, чем способность к сомнению». Этот принцип применим и здесь: каждое «улучшение» алгоритма — это лишь отсрочка неизбежной энтропии, и всегда найдется прод, который найдет способ заставить даже самый изящный алгоритм работать медленнее. Идея «ленивого» градиентного спуска, хоть и прагматична, лишь подтверждает, что в конечном итоге все сводится к поиску оптимального компромисса между теорией и практикой.

Что дальше?

Представленный алгоритм, как и многие другие «улучшения» в области онлайн-обучения, решает одну проблему, одновременно создавая предпосылки для новой. Минимизация переключений между обновлениями — благородная цель, однако стоит помнить: рано или поздно, кто-то обязательно найдёт способ заставить эту «лень» работать против системы. Динамическое сожаление, конечно, приятно, но в реальных условиях, где данные поступают непредсказуемо, а вычислительные ресурсы ограничены, каждый «оптимальный» шаг неминуемо обернётся компромиссом.

Вопрос о масштабируемости остаётся открытым. Алгоритм хорошо себя показывает в теоретических условиях, но стоит задуматься: что произойдёт, когда размерность данных достигнет астрономических величин? Очевидно, потребуется искать способы «причесать» градиенты, возможно, используя методы разреженного представления или квантования. Багтрекер уже предвкушает новые тикеты.

В конечном итоге, вся эта работа — лишь ещё один шаг в бесконечном цикле: разработка алгоритма, его внедрение, обнаружение проблем и повторная разработка. Мы не деплоим — мы отпускаем алгоритм в дикую природу, где он неизбежно столкнётся с суровой реальностью. И, скорее всего, ему потребуется не только «лень», но и хорошая доля удачи.

Оригинал статьи: https://arxiv.org/pdf/2601.15984.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-26 02:12