Планирование в мире Марковских процессов: Новый взгляд на оптимальную политику

Автор: Денис Аветисян

В статье предлагается оригинальный подход к планированию в Марковских процессах принятия решений, рассматривающий задачу как вывод оптимальной политики с использованием байесовского подхода.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

В сетчатых мирах демонстрируется взаимосвязь между стратегиями поведения и плотностью посещаемости, раскрывающая, как принятые решения формируют распределение агента в среде.

Предложен метод, позволяющий явно моделировать неопределенность в отношении оптимальной политики и избегать необходимости в регуляризации энтропии, интерпретируя масштаб вознаграждения как отражение неопределенности предпочтений.

Традиционные подходы к планированию в марковских процессах принятия решений (MDP) часто сталкиваются с трудностями при явном представлении неопределенности в оптимальной политике. В работе ‘MDP Planning as Policy Inference’ предложен новый взгляд, рассматривающий планирование MDP как байесовский вывод относительно политик, где политика выступает в роли скрытой переменной. Это позволяет построить апостериорное распределение, отражающее как оптимальные решения, так и степень неопределенности относительно наилучшего поведения, избегая необходимости в регуляризации на основе энтропии. Какие возможности открывает такое представление для разработки более надежных и адаптивных систем управления в сложных динамических средах?

За пределами детерминированного планирования: Эра стохастических политик

Традиционные подходы к принятию решений, такие как планирование на основе марковских процессов принятия решений (MDP), часто исходят из предположения о полностью детерминированной среде. Однако, реальный мир редко бывает предсказуемым. Неизбежная неопределенность, возникающая из-за неполной информации, случайных событий и непредсказуемости действий других агентов, существенно ограничивает применимость этих методов в практических сценариях. Представьте себе робота, которому необходимо ориентироваться в оживленной городской среде или алгоритм торговли на финансовом рынке — в обоих случаях абсолютная уверенность в исходе каждого действия является недостижимой иллюзией. Ограничения детерминированных моделей приводят к тому, что разработанные стратегии оказываются неэффективными или даже неработоспособными в условиях реальной, динамично меняющейся обстановки, подчеркивая необходимость разработки более гибких и устойчивых методов принятия решений.

Введение стохастических политик позволяет агентам успешно действовать в условиях неопределенности, что особенно важно для сложных систем реального мира. В отличие от традиционных детерминированных подходов, где каждое действие приводит к предсказуемому результату, стохастические политики определяют вероятностное распределение действий для каждой ситуации. Это означает, что агент не выбирает единственное действие, а случайным образом выбирает одно из нескольких возможных, каждое из которых имеет свою вероятность. Такой подход повышает устойчивость к шумам и неполной информации, позволяя агенту адаптироваться к изменяющимся условиям и находить оптимальные решения даже в ситуациях, когда точное предсказание будущего невозможно. В результате, системы, использующие стохастические политики, демонстрируют повышенную надежность и эффективность в различных областях, от робототехники и управления ресурсами до финансовых рынков и искусственного интеллекта.

Представление и обработка неопределенности, возникающей при использовании стохастических политик, требует принципиально новых подходов к организации политик и проведению логических выводов. Традиционные методы, основанные на дискретных состояниях и действиях, оказываются недостаточными для эффективной работы в сложных, непредсказуемых средах. Вместо этого, исследователи разрабатывают методы, использующие вероятностные распределения для представления действий, позволяя агентам выбирать оптимальные стратегии, учитывая различные возможные исходы. Особое внимание уделяется разработке алгоритмов, способных эффективно оценивать и обновлять эти распределения в процессе обучения, используя такие инструменты, как $Bayes Networks$ и $Monte Carlo Tree Search$ . Это позволяет агентам не только адаптироваться к изменяющимся условиям, но и предвидеть потенциальные риски и возможности, что критически важно для достижения надежных результатов в реальных приложениях.

На изображении представлены сетки миров, в которых детерминированные политики не соблюдаются.

Байесовский вывод и обучение политик: Преодоление неопределенности

Байесовский вывод предоставляет формализованный подход к рассуждениям в условиях неопределенности, позволяя агентам обновлять свои представления об оптимальной политике на основе наблюдаемых данных. В рамках данного подхода, политика рассматривается как случайная величина, описываемая априорным распределением вероятностей. Наблюдаемые данные, полученные в результате взаимодействия агента с окружающей средой, используются для вычисления апостериорного распределения, которое отражает обновленные знания агента о политике. Этот процесс обновления осуществляется с использованием теоремы Байеса, позволяющей комбинировать априорные знания с эмпирическими данными. Таким образом, агент способен адаптироваться к изменяющимся условиям и постепенно улучшать свою политику, основываясь на накопленном опыте и уменьшая неопределенность в процессе принятия решений.

Подход “Управление как Вывод” (Control-as-Inference) переформулирует задачу принятия решений как проблему байесовского вывода, рассматривая оптимальную политику как апостериорное распределение над возможными действиями. Вместо прямого поиска оптимальной политики, этот подход определяет политику как результат вывода, основанного на априорных знаниях о среде и наблюдаемых данных. Это позволяет объединить различные методы обучения с подкреплением в единую вероятностную структуру, что упрощает процесс обучения и обеспечивает более устойчивые результаты. В частности, $p(a|s) = \in t p(a|s, \pi) p(\pi|s) d\pi$ , где $p(a|s)$ — вероятность действия $a$ в состоянии $s$ , $p(a|s, \pi)$ — вероятность действия $a$ в состоянии $s$ при политике π, а $p(\pi|s)$ — апостериорное распределение над политиками в состоянии $s$ .

Представление оптимизации политики как задачи вероятностного вывода позволяет использовать методы аппроксимации для нахождения оптимальных решений даже в сложных и многомерных пространствах состояний. Такой подход позволяет оценивать вероятность различных действий, учитывая неопределенность в окружающей среде и ограничения, накладываемые на систему. Экспериментальные результаты демонстрируют, что производительность алгоритмов, основанных на вероятностном выводе, сопоставима с производительностью алгоритма Soft Actor-Critic (SAC), являющегося одним из передовых методов обучения с подкреплением, что подтверждает эффективность данного подхода к решению задач управления в сложных условиях.

Масштабируемый вывод с использованием вариационных методов

Метод вариационного последовательного Монте-Карло (Variational Sequential Monte Carlo, VSMC) представляет собой практический подход к аппроксимации байесовского вывода в задачах последовательного принятия решений. В отличие от точного байесовского вывода, который часто вычислительно затруднителен, VSMC использует вариационный вывод для получения приближенного распределения вероятностей состояния, позволяя эффективно оценивать неопределенность и обновлять убеждения агента по мере поступления новой информации. Этот метод особенно полезен в задачах с большим пространством состояний и действий, где точное решение недостижимо, и обеспечивает компромисс между точностью и вычислительной эффективностью, позволяя агенту принимать обоснованные решения в условиях ограниченных ресурсов.

Метод вариационного последовательного Монте-Карло обеспечивает эффективное вычисление ожидаемой доходности ( $E[R]$ ), являющейся ключевой метрикой для оценки производительности стратегии (policy). Вычисление ожидаемой доходности позволяет оценить среднюю награду, которую можно ожидать от применения данной стратегии в долгосрочной перспективе. Эффективность вычисления достигается за счет использования вариационных приближений и методов Монте-Карло, что позволяет снизить вычислительные затраты по сравнению с точными методами Байесовского вывода. Точная оценка $E[R]$ критически важна для сравнения различных стратегий и выбора оптимальной в задачах последовательного принятия решений.

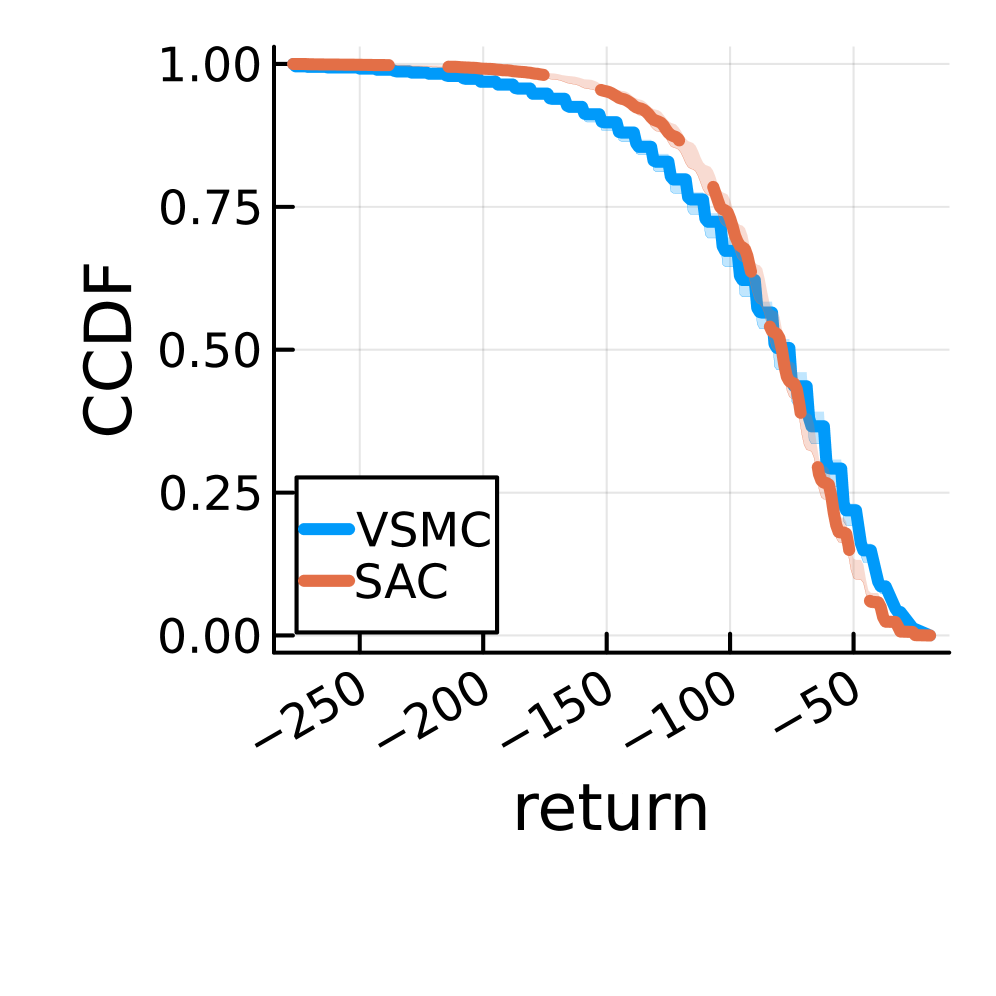
Применение метода вариационного последовательного Монте-Карло в задачах, таких как Blackjack, Triangle Tireworld и Academic Advising, подтверждает его эффективность в решении сложных, реальных задач. В этих областях, разработанный подход демонстрирует достижение показателей возврата по траектории, сопоставимых с результатами, полученными при использовании алгоритма Soft Actor-Critic (SAC). Это свидетельствует о практической применимости метода для оценки и оптимизации стратегий принятия решений в различных сферах, где требуется работа с неопределенностью и последовательными наблюдениями.

Распределения траекторий возврата в академическом консультировании для экземпляров 1-3 демонстрируют вариативность стратегий достижения целей.

Роль неопределенности предпочтений и исследования

Неопределенность в предпочтениях оказывает существенное влияние на необходимость использования стохастических политик в системах искусственного интеллекта. Когда агент сталкивается с множеством потенциальных целей, а не с одной четко определенной, детерминированная политика может оказаться неэффективной, поскольку она ориентирована на достижение лишь одного конкретного результата. Стохастическая политика, напротив, позволяет агенту исследовать различные варианты действий и адаптироваться к изменяющимся предпочтениям, повышая вероятность успешного достижения желаемого результата в условиях неполной информации. Это особенно важно в задачах, где цели могут быть скрытыми или меняться со временем, требуя от агента гибкости и способности к адаптации, чтобы эффективно функционировать и максимизировать свою полезность.

Для эффективного обучения агентов в сложных средах, регуляризация энтропии играет ключевую роль в стимулировании исследования пространства действий и предотвращении застревания в локально оптимальных стратегиях. Этот метод добавляет к функции потерь штраф, пропорциональный энтропии политики, тем самым поощряя агента выбирать более разнообразные действия, даже если они кажутся менее перспективными на первый взгляд. Такой подход позволяет агенту открывать новые, потенциально более выгодные стратегии, которые могли бы остаться незамеченными при использовании исключительно жадных алгоритмов. Регуляризация энтропии особенно важна в ситуациях, когда агент сталкивается с неопределенностью в отношении своих предпочтений или когда пространство состояний велико и сложно для полного исследования, что способствует более надежному и адаптивному поведению в долгосрочной перспективе.

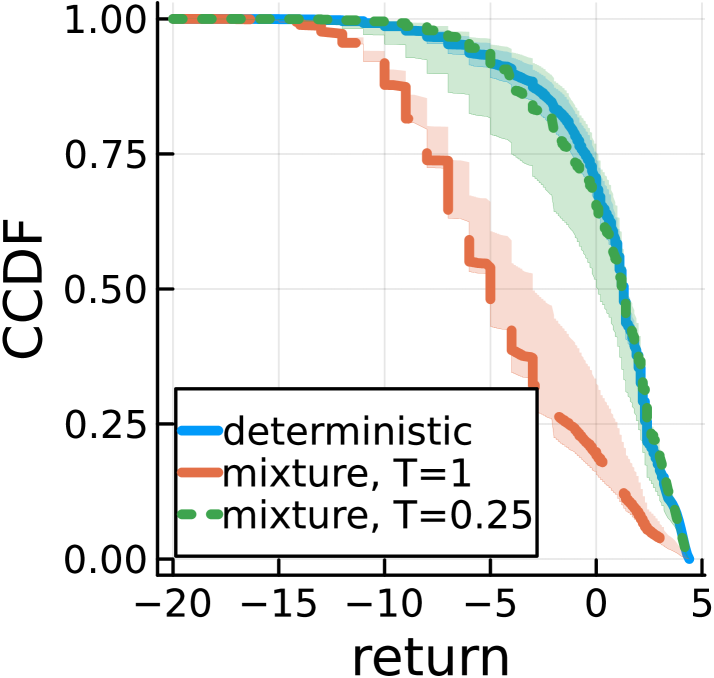
Методы, такие как сэмплирование по Томпсону, значительно расширяют возможности исследования в процессе обучения агента. В отличие от традиционных подходов, данный метод использует выборку из апостериорного распределения оптимальной политики, что позволяет агенту более эффективно учитывать неопределенность и находить решения, которые могут быть пропущены при использовании детерминированных стратегий. Результаты, полученные в среде моделирования академического консультирования, демонстрируют, что сэмплирование по Томпсону приводит к более широкому распределению возвратов, что свидетельствует о большей осведомленности агента о возможных долгосрочных последствиях своих действий по сравнению с алгоритмом SAC. Однако, в задаче “Triangle Tireworld” наблюдалось, что данный подход иногда приводил к снижению вероятности завершения задачи по сравнению с SAC, указывая на необходимость тонкой настройки параметров для достижения оптимальной производительности в различных средах.

Исследование демонстрирует, что планирование в марковских процессах принятия решений может быть эффективно представлено как байесовский вывод о политике. Такой подход позволяет явно учитывать неопределенность в отношении оптимальных стратегий, избегая необходимости в регуляризации энтропии. Вместо этого, масштаб вознаграждения интерпретируется как отражение неопределенности предпочтений. Как однажды заметил Марвин Мински: «Наиболее перспективные способы решения проблемы часто заключаются в переформулировке самой проблемы». Данная работа, представляя планирование как байесовский вывод, воплощает эту идею, предлагая элегантный способ преодоления сложностей, связанных с неопределенностью, и подчеркивая, что ясная структура определяет поведение системы.

Куда Ведет Дорога?

Представление планирования в Марковских процессах принятия решений как байесовского вывода о политике, несомненно, элегантно. Однако, как часто бывает, избавление от одного узла порождает новые переплетения. Необходимость явного моделирования неопределенности в предпочтениях, хотя и логична, переносит бремя сложности на другой уровень. Все ломается по границам ответственности — если не учитывать всю систему, то и надеяться на устойчивость бессмысленно. Предложенный подход, безусловно, позволяет избежать искусственного введения регуляризации энтропии, но возникает вопрос: не переносится ли неопределенность предпочтений в другие аспекты планирования, требуя аналогичного явного моделирования?

Следующим шагом представляется исследование возможности объединения данного подхода с методами иерархического обучения с подкреплением. Очевидно, что структура определяет поведение, и умение декомпозировать сложные задачи на более простые подзадачи, сохраняя при этом представление об общей неопределенности, может привести к значительному повышению эффективности. Кроме того, представляется перспективным исследование влияния различных априорных распределений над политиками на устойчивость и обобщающую способность полученных решений.

В конечном счете, ценность предложенного подхода заключается не только в решении конкретной задачи планирования, но и в переосмыслении самой природы процесса принятия решений. Всегда ли оптимальная политика должна быть детерминированной? И не является ли неопределенность не недостатком, а неотъемлемой частью реальности, которую необходимо учитывать для построения действительно надежных и адаптивных систем?

Оригинал статьи: https://arxiv.org/pdf/2602.17375.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-22 02:11