Поиск оптимальных решений в многомерном пространстве: новый подход

Автор: Денис Аветисян

Исследователи предлагают оригинальный алгоритм, использующий принципы дифференциальных игр, для эффективного поиска решений на невыпуклых Парето-фронтах.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал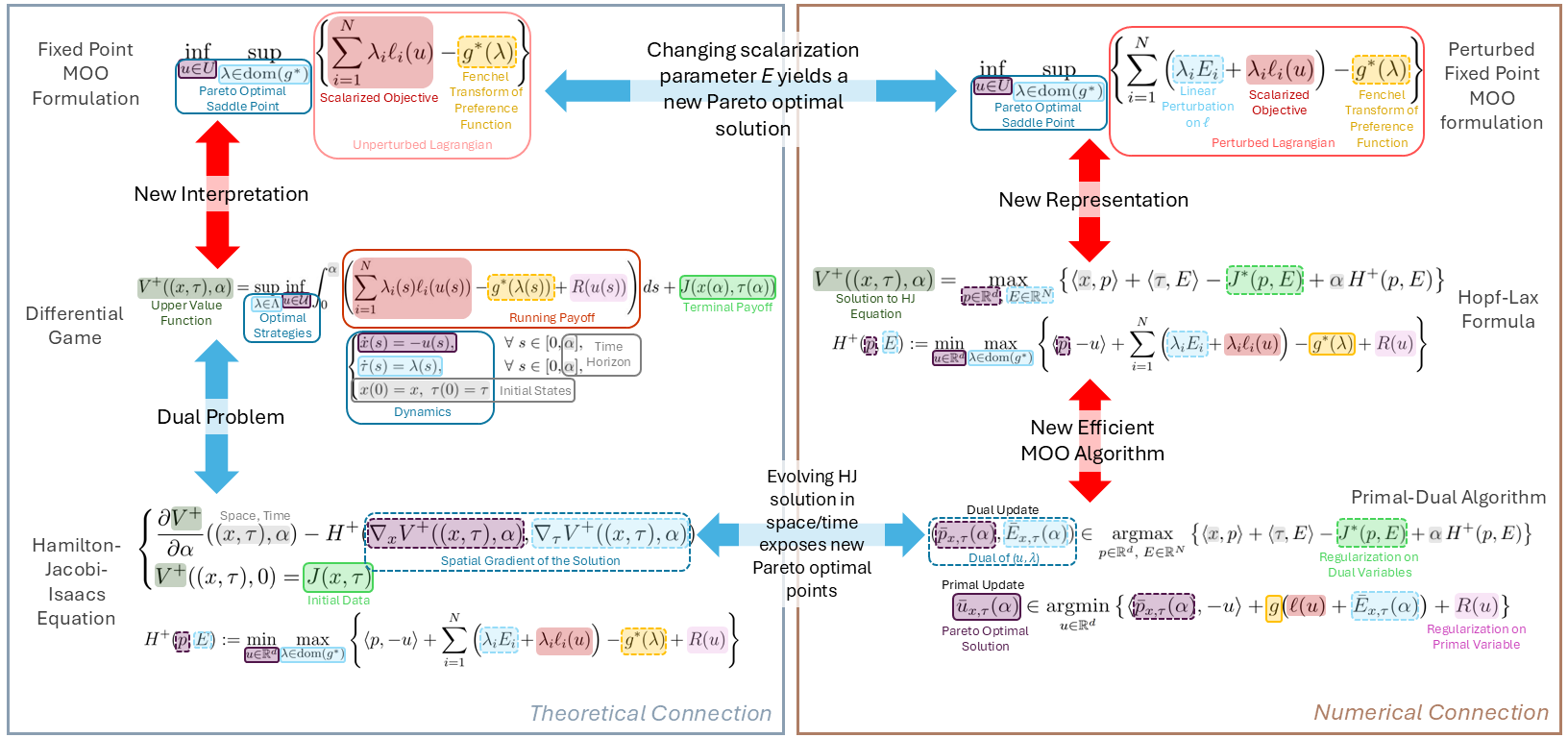

Эволюция парето-фронта описывается посредством дифференциальной игры и уравнения Гамильтона-Якоби, а представлением Хопфа-Лакса достигается эффективная примально-дуальная схема для численного исследования высокоразмерных, потенциально невыпуклых парето-фронтов, где цветовое кодирование указывает на эквивалентность величин между исходной и двойственной постановками задачи.

Представлен метод многоцелевой оптимизации, основанный на решении уравнения Гамильтона-Якоби с применением формулы Хопфа-Лакса и примитивно-дуального алгоритма.

Поиск оптимальных решений в многокритериальной оптимизации часто затруднен из-за проклятия размерности и невыпуклости Парето-фронта. В работе ‘Algorithms and Differential Game Representations for Exploring Nonconvex Pareto Fronts in High Dimensions’ предложен новый подход, основанный на теории дифференциальных игр и представлении Хопфа-Лакса, для исследования Парето-фронтов высокой размерности. Разработанный метод позволяет эффективно аппроксимировать Парето-фронт, используя параметризованную игру с нулевой суммой и применив разработанный примально-дуальный алгоритм. Способны ли предложенные алгоритмы масштабироваться на еще более сложные задачи многокритериальной оптимизации и открыть новые возможности для принятия решений в различных областях?

Определение Многокритериальной Оптимизации: Поиск Компромисса

Многие задачи, возникающие в реальном мире — от проектирования инженерных систем до управления финансовыми портфелями и планирования логистики — требуют одновременной оптимизации нескольких, зачастую противоречивых целей. Например, при разработке автомобиля необходимо учитывать не только его экономичность и мощность, но и безопасность, комфорт и стоимость. Попытка максимизировать все эти показатели одновременно сталкивается с неизбежным компромиссом: улучшение одного параметра может привести к ухудшению другого. Такие ситуации требуют поиска не единственного оптимального решения, а целого набора вариантов, каждый из которых представляет собой наилучший компромисс между различными целями, что значительно усложняет процесс принятия решений и требует применения специализированных методов оптимизации.

В задачах многокритериальной оптимизации, или MOO-задачах, традиционный подход, направленный на поиск единственного наилучшего решения, становится неэффективным. Вместо этого, акцент смещается на формирование множества Парето-оптимальных решений. Данные решения характеризуются тем, что улучшение по одному критерию неизбежно приводит к ухудшению по другому, что отражает компромиссный характер задачи. Множество Парето-оптимальных решений предоставляет возможность выбора наилучшего варианта, исходя из предпочтений принимающего решение лица, учитывая его приоритеты и допустимые потери по отдельным критериям. Такой подход позволяет более полно и гибко учитывать сложность реальных задач, где зачастую невозможно достичь идеального результата по всем показателям одновременно.

Успешное решение многокритериальных задач оптимизации неразрывно связано с эффективным управлением ограничениями, определяющими допустимые рамки поиска. Ограничения, будь то физические законы, бюджетные рамки или технические спецификации, существенно влияют на сложность и достижимость оптимальных решений. Предлагаемый подход направлен на преодоление этих трудностей посредством $\text{инновационного алгоритма}$ , который позволяет находить решения, удовлетворяющие всем заданным ограничениям, и одновременно оптимизировать несколько, зачастую противоречивых, целей. В отличие от традиционных методов, данный алгоритм динамически адаптируется к изменяющимся ограничениям и масштабируемым задачам, обеспечивая надежный и эффективный поиск Парето-оптимальных решений даже в сложных и многомерных пространствах.

Разработанный примально-дуальный алгоритм HJ/Hopf-Lax (·) точно восстанавливает истинный фронт Парето (обозначен пунктирной линией) для двумерной выпуклой задачи многокритериальной оптимизации с полуалгебраическим множеством допустимых решений менее чем за 0.1 секунды, при этом все найденные оптимальные решения лежат на границе допустимой области.

Ограничения и Допустимые Области: Формирование Пространства Решений

При практическом применении задач оптимизации часто возникает необходимость соблюдения так называемых полуалгебраических ограничений, которые определяют допустимую область поиска решений. Эти ограничения представляют собой неравенства, основанные на полиномиальных функциях, и формально описываются как комбинация полиномиальных неравенств и равенств. В общем виде, полуалгебраическое ограничение может быть выражено как $f(x) \leq 0$ , где $f(x)$ — полином от переменных $x$ . Ограничения данного типа возникают в различных областях, включая проектирование, экономику и машинное обучение, и существенно влияют на сложность и структуру пространства решений, ограничивая множество возможных оптимальных вариантов.

Ограничения, заданные в виде полиномиальных неравенств, существенно влияют на вычислительную сложность поиска оптимальных решений. Степень полиномов, количество переменных и число неравенств напрямую определяют размер и сложность допустимой области. Например, задача с $n$ переменными и $m$ полиномиальными ограничениями требует экспоненциальных ресурсов для точного решения в общем случае. Следовательно, эффективные алгоритмы оптимизации должны учитывать эти факторы и использовать стратегии для сокращения пространства поиска, такие как декомпозиция ограничений или использование приближенных методов для задач высокой размерности.

Алгоритм обеспечивает эффективную обработку полуалгебраических ограничений, гарантируя, что все найденные Парето-оптимальные решения располагаются на границе допустимой области. Это достигается за счет применения специализированных методов, которые позволяют точно идентифицировать и учитывать ограничения при поиске оптимальных решений. Расположение решений на границе означает, что любое улучшение по одному из критериев оптимизации неизбежно приведет к нарушению хотя бы одного из ограничений, что подтверждает оптимальность найденных решений в рамках заданных условий. Такой подход позволяет существенно сократить область поиска и повысить эффективность алгоритма при решении многокритериальных задач оптимизации с ограничениями.

Примально-Дуальный Подход: Итеративное Решение

Примально-дуальный алгоритм представляет собой надежный метод решения задач многокритериальной оптимизации (MOO) с ограничениями. Данный подход, основанный на теории дуальности Лагранжа, позволяет эффективно исследовать пространство допустимых решений, находя компромиссные варианты, удовлетворяющие заданным ограничениям. В отличие от традиционных методов, примально-дуальный алгоритм не требует явного определения функции ценности и способен обрабатывать задачи с большим числом ограничений и переменных, обеспечивая устойчивое схождение к оптимальному решению в условиях сложной оптимизационной среды. Ключевым преимуществом является возможность учета как целей оптимизации, так и ограничений, что делает его применимым в широком спектре задач, включая планирование ресурсов, управление рисками и проектирование систем.

Алгоритм, основанный на чередовании обновления примальных и дуальных переменных, обеспечивает эффективное исследование пространства решений, ограниченного заданными условиями. На каждой итерации происходит корректировка значений примальных переменных (представляющих непосредственные решения задачи) и дуальных переменных (определяющих штрафы за нарушение ограничений). Такой подход позволяет алгоритму последовательно приближаться к оптимальному решению, учитывая как целевые функции, так и ограничения, и избегать выхода за рамки допустимой области. Чередование обновлений способствует стабилизации процесса и повышает скорость сходимости к решению, особенно в задачах с большим числом ограничений и переменных.

Ключевым элементом алгоритма является функция предпочтений Softmax, обеспечивающая взвешивание различных целей оптимизации. Она позволяет находить компромиссные решения в задачах с несколькими противоречивыми критериями, назначая каждому возможному решению вероятность, зависящую от его соответствия заданным целям. Использование Softmax позволяет эффективно масштабировать алгоритм до пространства решений размерностью до d=100, что делает его применимым к задачам высокой размерности, где традиционные методы могут оказаться вычислительно неэффективными. Функция $Softmax(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}}$ нормализует значения, обеспечивая вероятностное распределение.

Представление Хопфа-Лакса и Уравнение Гамильтона-Якоби: Влияние и Точность

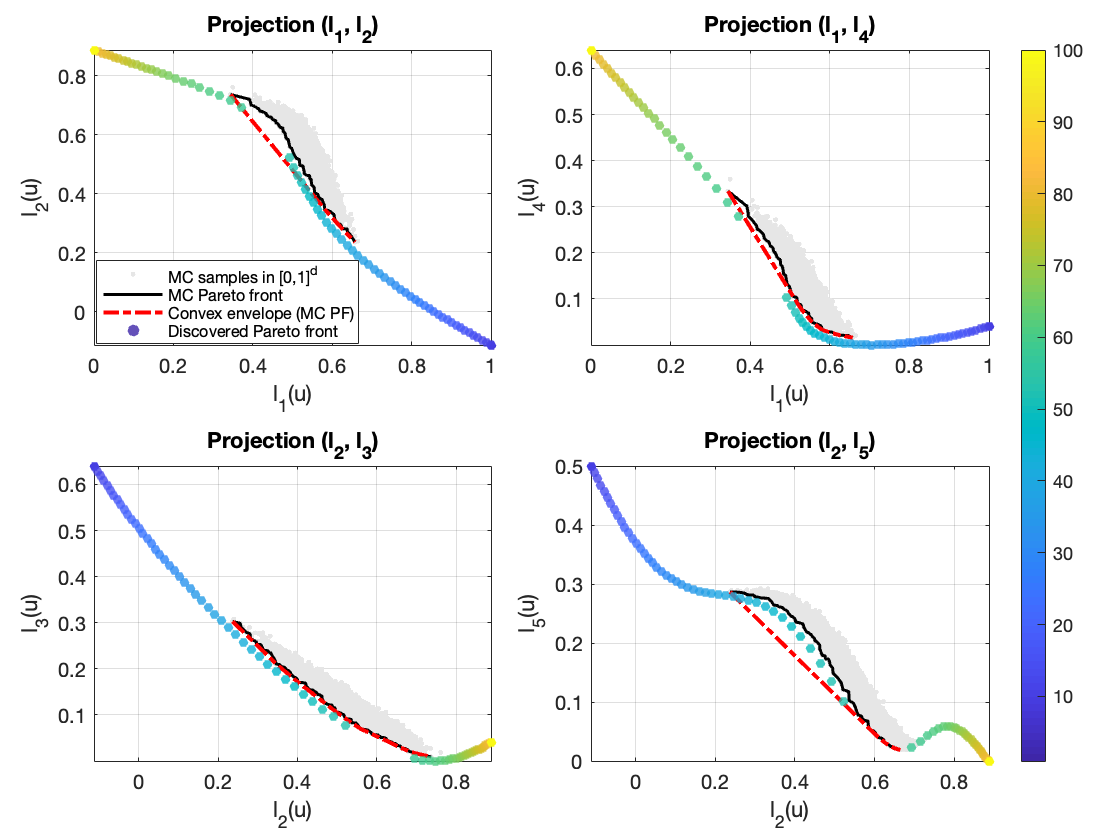
Представление Хопфа-Лакса обеспечивает фундаментальную связь между паретовским фронтом и уравнением Гамильтона-Якоби. Эта связь позволяет трансформировать задачу оптимизации в решаемое частное дифференциальное уравнение, что значительно упрощает определение оптимальных решений. Использование данного представления позволяет не только эффективно характеризовать паретовский фронт, но и аналитически подтверждать качество полученных парето-оптимальных решений. В частности, для двухмерной задачи многокритериальной оптимизации с ограничениями, основанной на выпуклых функциях, точное восстановление истинного паретовского фронта достигается менее чем за 0.1 секунды, демонстрируя высокую эффективность предложенного подхода и его применимость к задачам с увеличением числа целей, вплоть до N=5.

Установление связи между представлением Хопфа-Лакса и уравнением Гамильтона-Якоби позволяет преобразовать задачу оптимизации в решаемое частное дифференциальное уравнение. Это, в свою очередь, обеспечивает эффективную характеристику оптимальных решений и позволяет с высокой точностью восстановить истинный фронт Парето. В частности, для двухмерной задачи многокритериальной оптимизации с ограничениями и выпуклой функцией, точное восстановление фронта Парето достигается менее чем за 0.1 секунды, что демонстрирует вычислительную эффективность данного подхода. Преобразование задачи в форму, пригодную для решения с помощью методов решения частных дифференциальных уравнений, открывает возможности для анализа и получения точных решений, недоступных при использовании традиционных методов оптимизации.

Предложенное представление позволяет аналитически обосновать и подтвердить качество полученных парето-оптимальных решений. Исследования показали, что алгоритм успешно справляется с задачами, включающими до пяти целевых функций (N=5), что демонстрирует его масштабируемость и надежность. Возможность аналитической верификации является ключевым преимуществом, поскольку позволяет не только оценить точность полученных результатов, но и выявить потенциальные ошибки или неточности в процессе оптимизации. Это особенно важно в сложных многокритериальных задачах, где традиционные методы могут быть подвержены погрешностям или требовать значительных вычислительных ресурсов для подтверждения адекватности полученных решений.

Представленная работа демонстрирует, что эффективное исследование невыпуклых парето-фронтов в многомерных пространствах требует взгляда на систему как на единое целое. Оптимизация, как и в любой сложной системе, создает новые точки напряжения, требующие комплексного подхода. Сергей Соболев заметил: «Математика — это не только язык, но и искусство видеть структуру в хаосе». Эта фраза прекрасно отражает суть представленного исследования, где применение дифференциальных игр и формулы Хопфа-Лакса позволяет увидеть скрытую структуру в сложных оптимизационных задачах, превращая хаос множественных целей в упорядоченное исследование парето-оптимальных решений. Подобный подход подчеркивает, что архитектура системы, в данном случае алгоритма, определяет её поведение во времени.

Куда же дальше?

Представленный подход, опираясь на аппарат дифференциальных игр и формулу Хопфа-Лакса, безусловно, открывает новые горизонты в исследовании невыпуклых паретовских фронтов. Однако, элегантность математической конструкции не должна заслонять фундаментальную сложность оптимизации в высоких размерностях. Каждая новая зависимость от конкретной реализации алгоритма — это скрытая цена свободы от вычислительных ограничений. Вопрос о масштабируемости, столь важный для практических приложений, остается открытым, требуя более глубокого анализа асимптотического поведения предложенного примально-дуального метода.

Особого внимания заслуживает взаимодействие между структурой алгоритма и характером решаемой задачи. Неизбежно возникает вопрос о робастности — насколько хорошо предложенный подход адаптируется к изменениям в целевых функциях или ограничениях? Поиск универсальных стратегий, не требующих значительной перестройки при незначительных модификациях задачи, представляется перспективным направлением исследований. Структура определяет поведение, и лишь понимание этой связи позволит создать действительно устойчивые и эффективные алгоритмы.

В конечном счете, успех данного направления зависит не только от развития математического аппарата, но и от интеграции с другими подходами в области многокритериальной оптимизации. Смелые гипотезы о возможности построения самообучающихся алгоритмов, способных автоматически адаптироваться к специфике решаемой задачи, остаются предметом для дальнейших размышлений и экспериментов. Именно в этой диалектике между теорией и практикой и кроется истинный потенциал развития данного направления.

Оригинал статьи: https://arxiv.org/pdf/2602.11515.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-14 04:10