Предсказание в условиях манипуляций: новый подход к устойчивости моделей

Автор: Денис Аветисян

В статье представлен инновационный метод прогнозирования, обеспечивающий стабильность и надежность моделей в динамичных средах, подверженных стратегическим манипуляциям со стороны участников.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал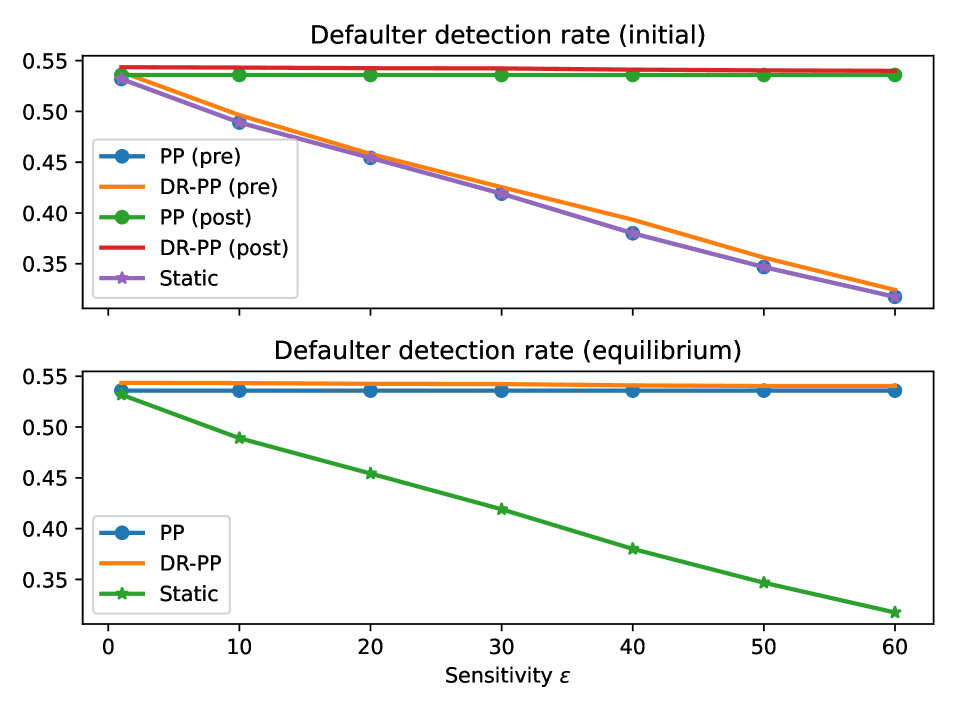

Временные и стационарные характеристики предсказания с учетом производительности демонстрируют, что робастный к изменениям распределения подход (DR-PP) превосходит стандартное предсказание с учетом производительности (PP) как в переходном процессе, так и в установившемся состоянии, в то время как фиксированный статический классификатор оказывается неэффективным при адаптации к смещенному распределению данных.

Разработанная методика использует робастную оптимизацию с нечеткостью Вассерштейна для смягчения влияния преднамеренных искажений данных и повышения устойчивости к стратегическому поведению.

Появление предсказательных моделей часто приводит к стратегической адаптации агентов, искажая исходное распределение данных и снижая эффективность прогнозов. В данной работе, посвященной ‘Wasserstein Distributionally Robust Performative Prediction’, предложен новый подход к решению этой проблемы, основанный на оптимизации с учетом наихудшего случая в рамках неоднозначности Вассерштейна. Предложенная методика позволяет находить устойчивые предсказательные модели, минимизирующие влияние стратегических манипуляций и обеспечивающие стабильность в динамически меняющихся условиях. Не приведет ли это к созданию более надежных и эффективных систем прогнозирования в различных областях, от финансов до кредитного скоринга?

Неуловимость Предсказаний: Когда Данные Изменяются

Традиционные методы машинного обучения основываются на предположении о стационарности распределения данных, то есть о его неизменности во времени. Однако, в реальных условиях, это условие часто не выполняется. Многие системы, функционирующие в динамичных средах — от рекомендательных систем до алгоритмов ценообразования — сталкиваются с постоянно меняющимися данными. Например, предпочтения пользователей в интернет-магазине эволюционируют, а рыночные цены подвержены колебаниям. Такое нарушение стационарности приводит к снижению точности моделей, поскольку они обучаются на устаревших данных и не способны адекватно реагировать на новые тенденции. Это особенно критично в ситуациях, где от точности предсказаний зависит принятие важных решений или функционирование сложных систем. Поэтому, разработка методов, способных адаптироваться к меняющимся данным, является одной из ключевых задач современного машинного обучения.

Появление “прогностического влияния” — ситуации, когда само внедрение модели прогнозирования оказывает воздействие на поведение агентов, — приводит к возникновению петли обратной связи, вызывающей смещение распределения данных. Изначально модель обучается на определенном наборе данных, отражающем существующее состояние системы. Однако, после внедрения, ее прогнозы могут изменить действия агентов, что, в свою очередь, меняет исходные данные, на которых обучалась модель. Этот процесс создает непрерывную динамику, в результате которой модель постоянно сталкивается с данными, отличными от тех, на которых она была обучена. Таким образом, стандартные методы машинного обучения, предполагающие статичность распределения данных, теряют свою эффективность, а необходимость разработки адаптивных и устойчивых алгоритмов становится особенно актуальной.

Традиционные методы машинного обучения, такие как минимизация эмпирического риска, оказываются ненадежными при изменении исходного распределения данных. Это смещение, возникающее из-за влияния самой модели на поведение агентов и, как следствие, на данные, требует разработки более устойчивых алгоритмов. Предлагаемый подход обеспечивает сходимость и стабильность итеративных алгоритмов даже в динамически меняющихся условиях, гарантируя надежность предсказаний в реальных приложениях, где данные постоянно эволюционируют под воздействием модели.

Алгоритм дистрибуционно-устойчивой перформативной минимизации риска (Алгоритм 1) демонстрирует сходимость при различных значениях параметра [latex] \varepsilon [/latex]-чувствительности, при этом достижение численного нуля расстояния между итерациями указывает на завершение сходимости. — Алгоритм дистрибуционно-устойчивой перформативной минимизации риска (Алгоритм 1) демонстрирует сходимость при различных значениях параметра $\varepsilon$ -чувствительности, при этом достижение численного нуля расстояния между итерациями указывает на завершение сходимости.

Робастность через Неопределенность: Введение в DRO

Расширение подхода Эмпирической Минимизации Риска (ERM), оптимизация с учетом распределительной робастности (DRO) предполагает поиск решения, оптимального не для фиксированного распределения данных, а для наихудшего случая внутри заданного множества неопределенности (ambiguity set). Данное множество определяет допустимые отклонения от эмпирического распределения, полученного на обучающей выборке. Вместо минимизации риска только для наблюдаемых данных, DRO минимизирует максимальный риск, который может возникнуть при любом распределении, принадлежащем этому множеству. Это позволяет создавать модели, более устойчивые к изменениям в данных и менее подверженные переобучению, поскольку они готовятся к потенциальным отклонениям от предполагаемого распределения.

Распределённая робастная оптимизация (DRO) исходит из предположения о неизвестности истинного распределения данных, используемых для обучения модели. В отличие от традиционных методов, которые оптимизируются под конкретное эмпирическое распределение, DRO учитывает возможность отклонений от этого распределения. Это достигается путём поиска решения, которое обеспечивает приемлемую производительность не только для наблюдаемых данных, но и для широкого спектра возможных распределений, близких к эмпирическому. Такой подход позволяет повысить устойчивость модели к шумам и нетипичным входным данным, что критически важно для практических приложений, где истинное распределение данных часто не полностью известно или может меняться со временем.

В рамках Distributionally Robust Optimization (DRO) расстояние Вассерштейна выступает в качестве эффективной метрики для количественной оценки расхождения между эмпирическим распределением данных и рассматриваемыми кандидатскими распределениями. Это позволяет проводить более точную и детализированную оценку рисков, связанных с неопределенностью данных. Наши алгоритмы, использующие расстояние Вассерштейна, демонстрируют сходимость в пределах 20 итераций для различных уровней чувствительности (epsilon), что подтверждает их стабильность и эффективность в задачах оптимизации с учетом неопределенности.

Метод градиентного спуска с учетом робастности к распределению (Алгоритм 2) демонстрирует сходимость при различных значениях параметра [latex] \varepsilon [/latex]-чувствительности. — Метод градиентного спуска с учетом робастности к распределению (Алгоритм 2) демонстрирует сходимость при различных значениях параметра $\varepsilon$ -чувствительности.

Поиск Стабильности в Динамичном Мире

Прямая оптимизация по наихудшему распределению данных представляет собой вычислительно сложную задачу, особенно в условиях высокой размерности пространства параметров и неопределенности распределения. Это связано с необходимостью рассмотрения бесконечного множества возможных распределений и вычисления оптимального решения для каждого из них. Для упрощения этой задачи часто применяются методы релаксации Лагранжа. Данный подход позволяет трансформировать исходную сложную задачу в более управляемую, путем введения дополнительных ограничений и использования двойственной задачи. Релаксация Лагранжа разбивает исходную задачу на серию более простых подзадач, которые могут быть решены итеративно, что существенно снижает вычислительную сложность и обеспечивает возможность нахождения приближенного оптимального решения за приемлемое время. Ключевым аспектом является правильный выбор множителей Лагранжа, определяющих степень штрафа за нарушение ограничений.

Теория сильного дуализма играет ключевую роль в обосновании метода Лагранжевой релаксации. Она гарантирует, что оптимальное решение, полученное в результате релаксации, соответствует оптимальному решению исходной задачи, несмотря на преобразования, внесенные в процесс оптимизации. В частности, сильный дуализм обеспечивает совпадение оптимальных значений исходной и двойственной задач, что позволяет использовать двойственную задачу для эффективного нахождения оптимального решения. Это особенно важно в контексте робастной оптимизации, где необходимо обеспечить стабильность решения при изменениях входных данных и неопределенности. Следовательно, доказательство сильного дуализма для конкретной задачи является необходимым условием для корректного применения Лагранжевой релаксации и уверенности в качестве полученного решения.

Для нахождения параметрически устойчивой точки — параметра модели, минимизирующего риск при изменении распределения данных — используются итеративные алгоритмы, такие как повторная минимизация риска (Repeated Risk Minimization) и повторный градиентный спуск (Repeated Gradient Descent). Теоретически доказано, что расстояние между параметрами устойчивой точки и глобальным оптимальным параметром, а также разрыв между рисками в этих точках, ограничены. В частности, установлены границы для $||w^<i> - w||$ и $|L(w^</i>) - L(w)|$ , где $w^*$ — глобальный оптимум, а $w$ — устойчивая точка, а $L$ — функция потерь. Эти границы позволяют оценить компромисс между робастностью и производительностью модели в динамически меняющейся среде.

При адаптации к смещенному распределению, метод DR-PP и PP демонстрируют высокую точность выявления нарушителей, при этом регуляризация [latex] \\lambda(\\theta)=\\lambda_{c}+0.1\\|\\theta\|^{2} [/latex] обеспечивает стабильность обучения на протяжении 2020 итераций. — При адаптации к смещенному распределению, метод DR-PP и PP демонстрируют высокую точность выявления нарушителей, при этом регуляризация $\\lambda(\\theta)=\\lambda_{c}+0.1\\|\\theta\|^{2}$ обеспечивает стабильность обучения на протяжении 2020 итераций.

Практическое Применение и Реальные Результаты

Логистическая регрессия, в сочетании с методами регуляризации, давно зарекомендовала себя как надежный инструмент для оценки кредитного риска. Этот подход позволяет создавать модели, способные прогнозировать вероятность невозврата кредита на основе различных факторов, таких как кредитная история, уровень дохода и занятость. Регуляризация, в свою очередь, помогает предотвратить переобучение модели, делая ее более устойчивой к новым данным и повышая точность прогнозов. В сфере кредитования, где даже небольшая ошибка может привести к значительным финансовым потерям, стабильность и надежность модели имеют первостепенное значение, и сочетание логистической регрессии с регуляризацией обеспечивает необходимую основу для принятия обоснованных решений.

Даже тщательно откалиброванные модели машинного обучения, используемые для оценки рисков, могут быть подвержены искажениям из-за преднамеренных действий оцениваемых. Агенты, стремящиеся получить более выгодные условия, способны изменять свое поведение, чтобы выглядеть менее рискованными, что приводит к неверной оценке их кредитоспособности. Этот феномен, известный как стратегическая манипуляция признаками, представляет серьезную угрозу для точности прогнозов, поскольку модель, обученная на искаженных данных, может ошибочно классифицировать неблагонадежных заемщиков как надежных. Подобные манипуляции способны существенно снизить эффективность моделей в реальных условиях, особенно в динамично меняющихся средах, где поведение агентов постоянно адаптируется.

Дистрибутивная робастность (DRO) представляет собой перспективный подход к смягчению последствий стратегической манипуляции признаками, которая может существенно снизить точность моделей оценки рисков, например, в сфере кредитования. Исследования показывают, что применение DRO, в частности, алгоритма DR-PP, позволяет значительно повысить точность выявления дефолтов и обеспечить более надежные прогнозы в динамично меняющихся условиях. В ходе экспериментов DR-PP демонстрирует стабильное превосходство над традиционным пост-процессингом (PP), показывая повышенную устойчивость к попыткам преднамеренного искажения информации с целью снижения воспринимаемого риска. Это делает DRO ценным инструментом для создания более надежных и устойчивых моделей в ситуациях, где агенты могут активно влиять на входные данные.

Алгоритм 1 демонстрирует стабильную производительность в процессе оптимизации (сплошные синие линии) и сохраняет её после развертывания классификатора, несмотря на изменение распределения данных (пунктирные зеленые линии) при стратегической чувствительности [latex] \varepsilon = 100 [/latex]. — Алгоритм 1 демонстрирует стабильную производительность в процессе оптимизации (сплошные синие линии) и сохраняет её после развертывания классификатора, несмотря на изменение распределения данных (пунктирные зеленые линии) при стратегической чувствительности $\varepsilon = 100$ .

Исследование, представленное в данной работе, стремится к созданию моделей, устойчивых к намеренным искажениям данных со стороны заинтересованных сторон. Авторы предлагают подход, основанный на оптимизации с учётом неопределённости, используя расстояние Вассерштейна для определения допустимого диапазона возможных распределений. Это позволяет не только повысить надёжность предсказаний, но и обеспечить стабильность системы в условиях динамичного окружения. В этом контексте, слова Григория Перельмана: «Если не можешь решить задачу, упрости её», особенно актуальны. Ведь суть предлагаемого метода — не в усложнении модели, а в её очищении от избыточной чувствительности к внешним воздействиям, в стремлении к элегантной простоте, способной противостоять хаосу.

Что дальше?

Предложенный подход, использующий робастную оптимизацию с использованием расстояния Вассерштейна, лишь обозначает границы проблемы, а не разрешает её. Стабильность модели в условиях стратегического воздействия — иллюзия, пока не учтены все возможные адаптации агентов. Попытка «закрыть» пространство манипуляций — тщетное усилие; агенты всегда найдут лазейки, а сама борьба с ними неизбежно усложнит модель, приближая её к неразрешимости.

Более продуктивным представляется отказ от попыток полного подавления стратегического поведения. Вместо этого, необходимо исследовать возможности взаимодействия с ним, рассматривая агентов не как противников, а как часть динамической системы. Ключевым вопросом является не «как защититься от манипуляций», а «как использовать их для улучшения предсказаний».

Следующим шагом видится разработка алгоритмов, способных к самообучению в условиях непрерывной адаптации агентов, формируя своего рода «эволюционную» модель предсказания. И, возможно, стоит признать, что абсолютная точность — недостижимый идеал. Достаточность — вот критерий, который следует принять, а простота — высшая форма изящества.

Оригинал статьи: https://arxiv.org/pdf/2602.06730.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-09 13:01