Риск и Неопределенность: Новый Взгляд на Принятие Решений

Автор: Денис Аветисян

Исследование предлагает инновационные методы оценки риска, основанные на фрактальной энтропии, для повышения эффективности принятия решений в условиях неопределенности.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Сравнение значений [latex]R^2[/latex] для различных моделей, основанных на энтропии дробного порядка, демонстрирует различия в их объясняющей способности и позволяет оценить эффективность каждого подхода. — Сравнение значений $R^2$ для различных моделей, основанных на энтропии дробного порядка, демонстрирует различия в их объясняющей способности и позволяет оценить эффективность каждого подхода.

Разработаны нормализованные меры риска на основе дробной энтропии (NEU-FE и NEU-FEV) и продемонстрирована их превосходная производительность при анализе данных индийского фондового рынка и применении методов машинного обучения.

Эффективное управление рисками и максимизация доходности портфеля требуют учета индивидуальных предпочтений инвесторов и адекватной оценки неопределенности. В работе ‘Normalized Fractional Order Entropy-Based Decision-Making Models under Risk’ предложены новые меры риска, основанные на нормализованной дробной энтропии, позволяющие более гибко моделировать отношение инвесторов к риску. Разработанные показатели — NEU-FE и NEU-FEV — демонстрируют улучшенные результаты при принятии инвестиционных решений, что подтверждается эмпирическим анализом данных индийского фондового рынка (NIFTY50) и применением методов машинного обучения. Способны ли предложенные модели стать основой для разработки более адаптивных и эффективных стратегий управления портфелем в условиях постоянно меняющейся рыночной конъюнктуры?

За пределами ожидаемой полезности: Ограничения традиционных мер риска

Традиционные методы оценки риска, зачастую опирающиеся на теорию ожидаемой полезности, испытывают значительные трудности при анализе сложных финансовых ландшафтов. Данные подходы, стремящиеся к упрощению неопределенности, не всегда адекватно отражают многообразие и взаимосвязь факторов, влияющих на инвестиционные решения. В условиях турбулентности рынка и нелинейных зависимостей между активами, стандартные модели могут давать неточные или даже вводящие в заблуждение результаты, недооценивая потенциальные убытки или переоценивая возможности. Особенно остро эта проблема проявляется при работе с экзотическими инструментами и при анализе системных рисков, когда традиционные предположения о нормальном распределении доходностей и независимости активов оказываются несостоятельными. В связи с этим, возникает необходимость в разработке и применении более совершенных методов оценки риска, учитывающих как количественные, так и качественные аспекты неопределенности.

Традиционные модели оценки рисков зачастую строятся на предположении о рациональности поведения инвесторов, что является упрощением реальной картины. Исследования в области поведенческой экономики демонстрируют, что принятие решений в условиях неопределенности подвержено многочисленным когнитивным искажениям и эвристикам. Инвесторы склонны к переоценке вероятности благоприятных исходов, боятся потерь сильнее, чем радуются равноценным выигрышам, и подвержены влиянию стадного инстинкта. Более того, степень неприятия риска варьируется от человека к человеку, и универсальное применение единой шкалы рисков может приводить к неадекватным оценкам и ошибочным инвестиционным решениям. Игнорирование этих факторов снижает точность прогнозов и эффективность стратегий управления рисками, подчеркивая необходимость разработки более реалистичных и гибких моделей, учитывающих психологические особенности инвесторов.

В связи с ограничениями существующих подходов к оценке рисков, возникает потребность в более совершенных инструментах, способных адекватно отражать предпочтения инвесторов и динамику рынков. Традиционные модели зачастую не учитывают поведенческие особенности, такие как нерациональность и различные уровни неприятия риска, что приводит к неточной оценке потенциальных потерь. Разрабатываемые альтернативные методы стремятся интегрировать психологические факторы и учитывать меняющиеся условия рынка, предлагая более реалистичную картину рисков и позволяя инвесторам принимать более взвешенные решения. Эти усовершенствованные инструменты, включающие в себя, например, модели, основанные на теории перспектив и эконометрические методы, способны учитывать асимметричные реакции на выигрыши и проигрыши, а также нелинейные зависимости между риском и доходностью, обеспечивая более точную и полную оценку инвестиционных возможностей.

Тепловая карта показывает, как изменения параметра qq влияют на величину NEU-FEV для акций NIFTY50.

Фрактальная энтропия: Улавливая нюансы неопределенности

Фрактальная энтропия представляет собой обобщение энтропии Шеннона, позволяющее более гибко моделировать неопределенность, учитывая различную степень чувствительности к вероятностным распределениям. В то время как классическая энтропия Шеннона $H(X) = - \sum_{i} p(x_i) \log_2 p(x_i)$ оценивает неопределенность на основе логарифма вероятностей, фрактальная энтропия использует параметр порядка α для модификации этого расчета. Значение α позволяет регулировать чувствительность к малым вероятностям; при $\alpha < 1$ фрактальная энтропия уделяет больше внимания этим вероятностям, что полезно в сценариях, где даже редкие события имеют значительное влияние. При $\alpha > 1$ влияние малых вероятностей снижается. Таким образом, фрактальная энтропия обеспечивает более детальное представление об уровне неопределенности, чем стандартная энтропия Шеннона, адаптируясь к специфике анализируемой задачи.

Модель EU-FE объединяет дробную энтропию с теорией ожидаемой полезности для создания более точной меры риска, учитывающей предпочтения инвесторов в сложных сценариях. Традиционная теория ожидаемой полезности предполагает, что инвесторы оценивают риски, основываясь на вероятностях и потенциальных исходах, однако она может быть ограничена в ситуациях с высокой неопределенностью или нелинейными предпочтениями. Интеграция дробной энтропии, которая позволяет более гибко оценивать неопределенность, позволяет модели EU-FE точнее отражать индивидуальные профили риска и предпочтения инвесторов, особенно в случаях, когда стандартные меры риска, такие как стандартное отклонение или Value-at-Risk, оказываются недостаточными. $EU_{FE} = \sum_{i} p_i U(x_i) \exp(-\alpha S_i)$ , где $p_i$ — вероятность исхода, $U(x_i)$ — функция полезности, $S_i$ — дробная энтропия исхода, а α — параметр, определяющий чувствительность к риску.

Интеграция фрактальной энтропии с ожидаемой полезностью (EU-FE модель) обеспечивает более детальную оценку рисков по сравнению с традиционными методами, такими как стандартное отклонение или Value-at-Risk (VaR). Традиционные подходы часто полагаются на упрощенные предположения о распределении вероятностей и склонности инвесторов к риску, что приводит к неточной оценке рисков в сложных сценариях. Фрактальная энтропия позволяет учитывать нелинейные зависимости и долгосрочные корреляции, предоставляя более точную картину неопределенности. Использование $EU_{FE}$ модели позволяет количественно оценить риск с учетом индивидуальных предпочтений инвестора и специфики рассматриваемого актива или портфеля, что повышает эффективность управления рисками и оптимизации инвестиционных стратегий.

Тепловая карта показателя NEU-FEV демонстрирует его динамику в зависимости от изменений [latex]qq[/latex] для отдельной акции NIFTY50. — Тепловая карта показателя NEU-FEV демонстрирует его динамику в зависимости от изменений $qq$ для отдельной акции NIFTY50.

NEU-FE: Надежная и сопоставимая мера риска

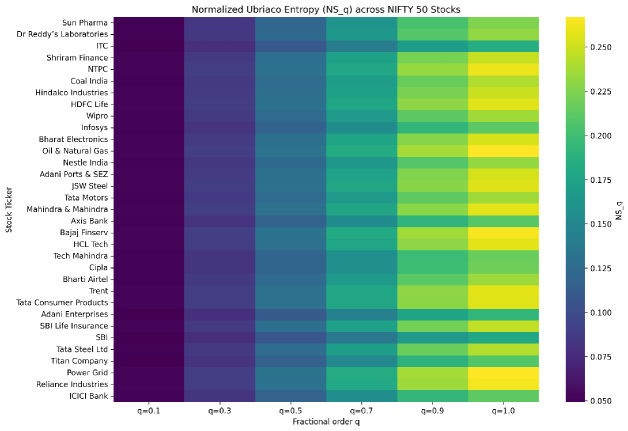
Модель Normalized Expected Utility-Fractional Entropy (NEU-FE) является расширением существующей EU-FE (Expected Utility-Fractional Entropy) модели и вводит процедуру нормализации. Данная нормализация направлена на повышение стабильности расчетов и обеспечение сопоставимости оценки рисков для различных инвестиционных портфелей. В отличие от базовой EU-FE, NEU-FE масштабирует значения $EU$ и $FE$ к общему диапазону, что позволяет корректно сравнивать риски портфелей с разным уровнем доходности и волатильности, а также снижает чувствительность к абсолютным значениям параметров. Процедура нормализации использует статистические методы для приведения результатов к единой шкале, что упрощает интерпретацию и анализ рисков.

В рамках модели NEU-FE успешно применена интеграция различных методов машинного обучения для прогнозирования финансовых рисков. В частности, использовались алгоритмы Random Forest, Ridge Regression, Lasso Regression и искусственные нейронные сети (Artificial Neural Networks). Эксперименты показали, что все перечисленные методы способны эффективно оценивать риски на основе модели NEU-FE, предоставляя альтернативные подходы к прогнозированию и анализу финансовых данных. Применение машинного обучения позволило автоматизировать процесс оценки рисков и повысить точность прогнозов по сравнению с традиционными методами.

Эмпирическая валидация модели NEU-FE на индексе NIFTY50 продемонстрировала ее практическую применимость и эффективность в реальных финансовых рынках. В частности, регрессия Lasso достигла почти идеального предсказания рисковых показателей, основанных на фракционной энтропии, полезности и дисперсии. Достигнутые значения коэффициента детерминации $R^2$ приблизились к 0.9999, а среднеквадратичная ошибка $MSE$ составила порядка 10⁻⁶, что подтверждает высокую точность модели в прогнозировании рисков на основе данных NIFTY50.

Учет изменчивости: Модель NEU-FEV

Модель NEU-FEV усовершенствует оценку рисков, расширяя рамки NEU-FE за счет включения дисперсии — меры разброса возможных исходов. В отличие от традиционных подходов, которые фокусируются на средних значениях, данная модель учитывает не только наиболее вероятный сценарий, но и диапазон потенциальных результатов, что позволяет более точно оценить степень неопределенности. По сути, NEU-FEV предлагает более полную картину риска, предоставляя информацию не только о том, что может произойти, но и о том, насколько сильно могут отклоняться фактические результаты от ожидаемых значений. Такой подход особенно важен в ситуациях, когда даже небольшие колебания могут иметь существенные последствия, позволяя более эффективно управлять рисками и принимать обоснованные решения.

Модель NEU-FEV значительно расширяет возможности оценки рисков, выходя за рамки простой вероятности неблагоприятного исхода. В отличие от традиционных подходов, она учитывает не только неопределенность, но и весь спектр возможных результатов, представляя собой более полную картину потенциальных потерь и прибылей. Это достигается путем анализа разброса значений — то есть, насколько сильно могут отличаться фактические результаты от ожидаемых. Учитывая дисперсию, модель позволяет более точно оценить потенциальный диапазон колебаний, предоставляя инвесторам и аналитикам возможность принимать более взвешенные и обоснованные решения, учитывающие не только средние значения, но и вероятность различных сценариев развития событий. Такой подход особенно важен в условиях высокой волатильности рынков, где понимание потенциального разброса результатов критически важно для управления рисками и оптимизации инвестиционных стратегий.

Проверка модели NEU-FEV на индексе NIFTY50 подтвердила ее способность предоставлять более детализированную и точную оценку рисков по сравнению с предшествующими моделями. В ходе тестирования, метод Lasso-регрессии продемонстрировал стабильно лучшие результаты, достигая коэффициента детерминации $R^2$ в 0.9999 и среднеквадратичной ошибки $MSE$ порядка 10⁻⁶. В то время как методы Random Forest и Ridge-регрессии показали значения $R^2$ в диапазоне 0.98-0.99 и >0.99 соответственно, искусственная нейронная сеть демонстрировала значительно более высокие значения $MSE$ , варьирующиеся от 10⁻³ до 10⁻². Полученные данные свидетельствуют о превосходстве модели NEU-FEV в сочетании с Lasso-регрессией для точной и надежной оценки финансовых рисков.

Исследование предлагает новые метрики риска, основанные на нормализованной дробной энтропии. Этот подход, как показывает анализ, превосходит существующие модели в принятии решений в условиях неопределенности. Сложность, неизбежная в финансовых моделях, требует строгого обоснования. Как говорил Макс Планк: «Наука — это бесконечный поиск, а не конечный набор фактов». Данное исследование демонстрирует стремление к упрощению сложных финансовых процессов, извлекая принципы из хаоса рыночных данных. Акцент на дробной энтропии позволяет более точно оценить риски, что особенно важно при построении эффективных стратегий принятия решений на фондовом рынке NIFTY50.

Что дальше?

Предложенные модели, основанные на нормализованной дробной энтропии, демонстрируют улучшение в оценке риска, но не избавляют от фундаментальной проблемы — неполноты информации. Улучшение показателей на данных NIFTY50 — это не триумф, а констатация того, что существующие методы несовершенны. Следующим шагом представляется не усложнение математического аппарата, а поиск более качественных данных, отражающих истинные рыночные настроения, а не их запоздалые отражения.

Перспективы лежат в области адаптивности. Модели, неподвижно закрепленные в текущих параметрах, обречены на устаревание. Необходима разработка самообучающихся систем, способных корректировать оценки риска в режиме реального времени, учитывая не только статистические закономерности, но и качественные факторы, ускользающие от количественного анализа. Это потребует интеграции методов машинного обучения с более глубоким пониманием поведенческой экономики.

Иронично, но наибольший прогресс может оказаться в отказе от стремления к абсолютно точным прогнозам. Достаточность, а не совершенство, должна стать ориентиром. Задача состоит не в том, чтобы предсказать будущее, а в том, чтобы создать инструменты, позволяющие разумно действовать в условиях неопределенности. Это требует не только математической точности, но и философской скромности.

Оригинал статьи: https://arxiv.org/pdf/2601.19715.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-28 06:32