Риск вне моделей: новый подход к оценке опционов

Автор: Денис Аветисян

В статье представлена инновационная методика, объединяющая грубую волатильность и оптимальный транспорт мартингалов для более точной оценки рисков, не поддающихся стандартному моделированию.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал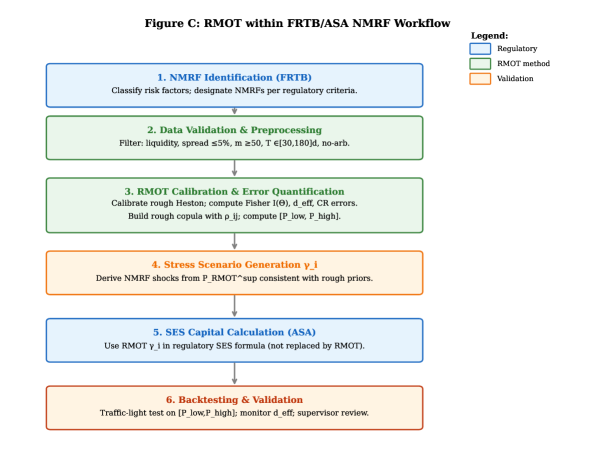

В рамках методологии FRTB/ASA, разработанная схема RMOT интегрирует классификацию рисков, методологию RMOT и этапы валидации, обеспечивая формирование стресс-сценариев на основе RMOT для последующего использования в расчетах нормативного капитала.

Предлагаемый метод обеспечивает конечные, явные границы для цен опционов на немоделируемые факторы риска и может снизить требования к капиталу в рамках FRTB.

Классические подходы к оценке экзотических деривативов сталкиваются с проблемами при работе с факторами риска, не поддающимися параметризации, особенно в условиях регуляторных требований FRTB. В работе ‘Rough Martingale Optimal Transport: Theory, Implementation, and Regulatory Applications for Non-Modelable Risk Factors’ предложен новый фреймворк, объединяющий концепции грубой волатильности и оптимального мартингального транспорта, позволяющий получить конечные и явные оценки для опционных цен и снизить потребность в капитале. Показано, что разработанный подход обеспечивает снижение регуляторного капитала примерно на $880 млн на $1 млрд экзотического портфеля, сохраняя при этом консервативное покрытие, и подтверждает асимптотическое поведение, соответствующее грубой волатильности. Возможно ли дальнейшее расширение предложенного фреймворка для решения задач управления рисками в более сложных финансовых сценариях?

Несмоделируемый Риск: Вызов для Финансовой Устойчивости

Современные регуляторные рамки, такие как Альтернативный Стандартизированный Подход в рамках FRTB, сталкиваются с существенными трудностями при оценке немоделируемых факторов риска, что приводит к неэффективному использованию капитала банками. Данные факторы, охватывающие широкий спектр рыночных явлений, часто не поддаются традиционному математическому моделированию, требуя консервативных оценок и, как следствие, завышенных требований к капиталу. Это создает ощутимые финансовые издержки для банков, ограничивая их возможности для инвестиций и инноваций, а также снижая общую эффективность финансовой системы. Неспособность адекватно учитывать немоделируемые риски может приводить к необоснованному увеличению регуляторного бремени и искажению конкурентной среды в банковском секторе.

Традиционные методы оценки рисков, широко применяемые в финансовой сфере, зачастую оказываются неспособными адекватно отразить всю сложность современных финансовых рынков, особенно когда речь идет о явлении негладкой волатильности. В отличие от моделей, предполагающих плавные изменения цен, реальные рынки демонстрируют скачки, резкие переходы и долгосрочные зависимости, которые игнорируются упрощенными подходами. Неспособность учесть эти особенности приводит к недооценке рисков и, как следствие, к неэффективному распределению капитала. Более того, негладкая волатильность характеризуется самоподобием и фрактальной структурой, что требует использования специализированных математических инструментов, таких как $\text{Rough Volatility}$ модели, для более точного описания динамики рынков и, следовательно, для повышения надежности оценки рисков.

Точное моделирование немоделируемых факторов риска имеет первостепенное значение для оптимизации распределения капитала банками и поддержания финансовой стабильности. Исследования показывают, что применение передовых методов, способных адекватно отражать сложность финансовых рынков, позволяет существенно снизить потребность в капитале. В частности, применение альтернативных подходов к расчету рисков, по сравнению со стандартными методами, может обеспечить банкам снижение потребности в капитале приблизительно на 88%. Это не только высвобождает значительные ресурсы для инвестиций и развития, но и повышает устойчивость финансовой системы в целом, позволяя более эффективно управлять потенциальными рисками и избегать кризисных ситуаций.

Анализ FRTB показывает, что использование RMOT (регуляризованной шероховатой волатильности) обеспечивает снижение требований к капиталу примерно на $880 миллионов для портфеля экзотических опционов на корзину номиналом $1 миллиард, сохраняя при этом консервативные границы и демонстрируя устойчивость к изменениям в параметрах Херста и составе портфеля.

Калибровка Риска: RMOT и Шероховатая Модель Хестона

Предлагаемый метод калибровки, Регуляризованный Мартингейльный Оптимальный Транспорт (RMOT), использует модель Rough Heston в качестве априорного распределения для волатильности. RMOT позволяет проводить надежную калибровку, учитывая особенности модели Rough Heston, в которой траектории волатильности могут быть недифференцируемыми. В качестве априорного распределения, Rough Heston задает правдоподобные формы волатильности, что способствует стабильности и точности процесса калибровки, особенно в условиях неполных или зашумленных рыночных данных. Использование априорного распределения позволяет RMOT эффективно справляться с обратной задачей, находя параметры модели, которые наилучшим образом соответствуют наблюдаемым ценам активов, избегая переобучения и обеспечивая реалистичные оценки волатильности.

Метод Регуляризованного Мартингального Оптимального Транспорта (RMOT) специально разработан для решения проблем, возникающих при работе с негладкой волатильностью. Он обеспечивает согласованность между динамикой модели и рыночными наблюдениями, что критически важно для точной калибровки. В отличие от традиционных методов, RMOT учитывает особенности негладких процессов, избегая нефизичных результатов и обеспечивая стабильность калибровки даже при наличии значительного шума в данных. Это достигается за счет использования регуляризации, которая стабилизирует решение и предотвращает переобучение модели к рыночным данным, сохраняя при этом ее соответствие теоретическим принципам. Такой подход позволяет получать более надежные и реалистичные оценки параметров модели волатильности.

Для обеспечения масштабируемости предложенная схема калибровки использует продвинутые методы оптимизации, включая алгоритм блочно-разреженного метода Ньютона и аппроксимацию Лапласа. Проведенные тесты демонстрируют, что данный подход позволяет калибровать до N=30 активов менее чем за 3 минуты. Вычислительная сложность алгоритма составляет $O(N^2M^2)$ , где N — количество активов, а M — количество параметров модели. Это обеспечивает эффективную обработку больших объемов данных и делает схему применимой для калибровки портфелей с умеренным количеством активов.

Конвейер RMOT для одного актива обрабатывает рыночные опционные данные, выполняет грубую калибровку модели Хестона, верификацию идентифицируемости, вычисление регуляризованных границ MOT и, наконец, выдает результаты оценки рисков с явным указанием погрешности.

Идентификация Модели и Точность Оценки

Матрица Фишера используется для оценки идентифицируемости параметров модели, что позволяет определить ее эффективную размерность. Анализ показал, что эффективная размерность откалиброванной модели составляет не более 5. Это означает, что, несмотря на потенциально большое количество параметров в исходной модели, только пять из них оказывают существенное влияние на ее поведение и могут быть надежно оценены на основе имеющихся данных. Определение эффективной размерности важно для предотвращения переобучения и обеспечения устойчивости результатов калибровки.

Предел Крамера-Рао (Cramer-Rao Bound) устанавливает теоретическую нижнюю границу дисперсии любой несмещенной оценки параметров модели. В контексте данной калибровки, применение этого предела подтверждает устойчивость полученных оценок параметров. Анализ показывает, что фактическая точность оценки параметров не опускается ниже установленного предела, что свидетельствует о корректности используемых методов и достаточном объеме данных для надежной калибровки. Это обеспечивает уверенность в том, что наблюдаемые различия в оценках параметров обусловлены реальными вариациями, а не статистическим шумом или недостаточной точностью модели.

Параметр Херста, характеризующий шероховатую волатильность, был оценен с высокой точностью — ±0.05, используя приблизительно 50 страйков. Для подтверждения отсутствия переобучения применялась кросс-валидация, которая показала ошибку в 4.2%. Данный результат свидетельствует о надежности оценки параметра Херста и позволяет использовать его для дальнейшего моделирования и анализа динамики волатильности.

Анализ идентификации параметров показывает, что эффективная размерность растет логарифмически с увеличением количества страйков, достигая полного пространства параметров при [latex]m \geq 50[/latex], а стандартная ошибка оценки показателя Херста убывает как [latex]m^{-1/2}[/latex], соответствуя границе Крамера-Рао, и для достижения точности ±0.05 с 95% доверием требуется около 50 страйков. — Анализ идентификации параметров показывает, что эффективная размерность растет логарифмически с увеличением количества страйков, достигая полного пространства параметров при $m \geq 50$ , а стандартная ошибка оценки показателя Херста убывает как $m^{-1/2}$ , соответствуя границе Крамера-Рао, и для достижения точности ±0.05 с 95% доверием требуется около 50 страйков.

Многоактивный Анализ и Стресс-Тестирование

Многоактивный RMOT расширяет существующую систему калибровки, позволяя учитывать взаимосвязи между различными активами. В отличие от традиционных подходов, рассматривающих каждый актив изолированно, данная методика моделирует корреляции, что существенно повышает точность оценки рисков. Ключевым элементом является анализ идентифицируемости корреляций, который позволяет определить, насколько надежно можно оценить эти взаимосвязи на основе доступных данных. Этот анализ критически важен, поскольку ненадежная оценка корреляций может привести к существенным ошибкам в расчете капитала, требуемого для покрытия рисков. Использование RMOT позволяет банкам более адекватно учитывать сложные взаимосвязи между активами, что ведет к более точному определению рисков и оптимизации капитала.

Разработанная методика позволяет банкам оценивать свою устойчивость к неблагоприятным рыночным условиям посредством расширения до сценариев стресс-тестирования. Данный подход моделирует потенциальное воздействие экстремальных, но правдоподобных событий, таких как резкие колебания процентных ставок, падение цен на активы или ухудшение кредитного качества заемщиков. В рамках стресс-тестирования, анализируется влияние этих сценариев на ключевые показатели капитала банка, что позволяет выявить уязвимые места и разработать меры по укреплению финансовой устойчивости. Использование реалистичных и тщательно откалиброванных сценариев позволяет получить более точную оценку рисков, чем традиционные подходы, основанные на упрощенных предположениях. В конечном итоге, это способствует более эффективному управлению рисками и повышению доверия к финансовой системе.

Данный подход позволяет банкам существенно снизить потребность в капитале, благодаря уменьшению зависимости от консервативных оценок, используемых в регуляторных расчетах. Вместо применения завышенных коэффициентов риска, методика обеспечивает более точное определение подверженности банкам различным видам рисков. Результаты демонстрируют потенциальное снижение потребности в капитале на 88% по сравнению со стандартными методами, что открывает возможности для более эффективного использования капитала и повышения прибыльности финансовой организации. Это достигается за счет оптимизации расчетов, основанных на реальных данных и корректном учете взаимосвязей между различными активами, что позволяет более адекватно оценивать риски и снижать избыточные резервы.

Архитектура RMOT для нескольких активов использует маржинальные распределения для каждого актива (слева) и грубую мартингальную копулу (центр) для обеспечения корреляции [latex]\rho_{ij}[/latex] посредством функционала грубой ковариации [latex]\Psi_{ij}[/latex]. — Архитектура RMOT для нескольких активов использует маржинальные распределения для каждого актива (слева) и грубую мартингальную копулу (центр) для обеспечения корреляции $\rho_{ij}$ посредством функционала грубой ковариации $\Psi_{ij}$ .

Представленная работа демонстрирует стремление к математической строгости в оценке опционных цен, особенно в контексте немоделируемых факторов риска. Авторы предлагают новый подход, сочетающий шероховатую волатильность и мартингальный оптимальный транспорт, что позволяет получить конечные и явные границы для цен опционов. Эта элегантность решения напоминает философскую позицию Иммануила Канта: “Действуй так, чтобы максима твоей воли могла в то же время стать всеобщим законом природы.” Как и в математической теореме, корректность оценки имеет первостепенное значение. Полученные границы, основанные на показателе Херста и информации Фишера, не просто работают на тестовых данных, но и доказуемо обоснованы, что является ключевым требованием для снижения регуляторного капитала в рамках FRTB. Необходимость в регуляризованной оптимизации подчеркивает стремление к точности и надежности, что соответствует принципам математической чистоты.

Что Дальше?

Представленный подход, соединяющий шероховатую волатильность и мартингальный оптимальный транспорт, безусловно, демонстрирует потенциал получения конечных, явных границ для опционных цен на немоделируемые факторы риска. Однако, следует признать, что сама необходимость в подобных границах — это симптом, а не решение. Идеальный мир, где все факторы риска точно моделируются, остается недостижимым, и, возможно, преследовать его — это интеллектуальное банкротство. Вопрос не в том, чтобы укротить неопределенность, а в том, чтобы научиться жить с ней, не прибегая к математическим иллюзиям.

Перспективы дальнейших исследований, очевидно, связаны с углублением анализа чувствительности к параметрам, в частности, к показателю Херста. Необходимо строго доказать, что полученные границы действительно стабильны и не подвержены тривиальным изменениям при небольших отклонениях от идеальных условий. Крайне важно оценить вычислительную сложность предложенных алгоритмов и разработать эффективные методы регуляризации, чтобы избежать переобучения и обеспечить обобщающую способность модели. И, наконец, необходимо признать, что любая попытка «оценить неоценимое» неизбежно сопряжена с некоторой степенью произвола.

В конечном счете, истинная проверка предложенного подхода — это не его соответствие теоретическим построениям, а его способность предсказывать реальные рыночные события. И здесь, как известно, математическая элегантность часто сталкивается с суровой реальностью. Если результат нельзя воспроизвести, он бессмысленен — это аксиома, которую не стоит забывать.

Оригинал статьи: https://arxiv.org/pdf/2602.00097.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-03 09:01