Сходимость в многомасштабных случайных системах: новый взгляд

Автор: Денис Аветисян

Исследование посвящено анализу поведения траекторий стохастических методов расщепления при решении обобщенных вариационных неравенств в системах с различными масштабами времени.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал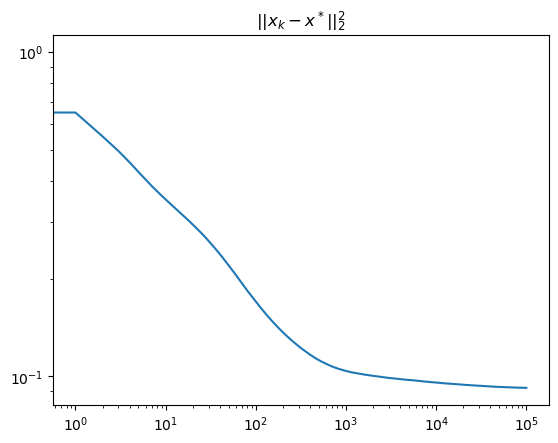

Оценка целесообразности демонстрирует сходимость к истинному значению, подтверждая эффективность предложенного подхода к решению задачи.

В работе доказана Cesaro-сходимость траекторий и установлена конечность сложности дискретной численной схемы для решения задач, связанных с максимальными монотонными операторами.

Несмотря на широкое применение стохастических методов в оптимизации и теории игр, анализ сходимости для систем с мультимасштабными эффектами остается сложной задачей. В данной работе, посвященной ‘Asymptotic behaviour of coupled random dynamical systems with multiscale aspects’, исследуется асимптотическое поведение класса связанных случайных динамических систем, возникающих при решении обобщенных вариационных неравенств. Показано, что траектории демонстрируют сходимость по Чезаро, а также установлены скорости сходимости, зависящие от функции зазора, и доказан принцип больших отклонений, описывающий экспоненциальную концентрацию траекторий вокруг множества решений. Каким образом полученные результаты могут быть применены к разработке эффективных численных алгоритмов для задач оптимизации и управления, учитывающих неопределенность и мультимасштабность?

Постижение Стохастических Систем: Вызов Неопределенности

Многие реальные системы, от колебаний популяций до финансовых рынков, демонстрируют стохастическую динамику, то есть их развитие определяется случайными факторами. Это означает, что точное предсказание будущего состояния системы невозможно, поскольку даже при полном знании начальных условий случайные воздействия вносят непредсказуемую составляющую. $P(x,t|x_0,t_0)$ — вероятность достижения состояния x в момент времени t, при заданном начальном состоянии $x_0$ в момент времени $t_0$ , описывает лишь распределение вероятностей, а не конкретную траекторию. Вследствие этого, традиционные детерминированные методы моделирования оказываются неэффективными, и исследователям приходится прибегать к вероятностным подходам и статистическому анализу для понимания и прогнозирования поведения таких систем, концентрируясь на средних значениях и вероятностных характеристиках, а не на точных решениях уравнений.

Многие сложные системы, от финансовых рынков до биологических процессов, характеризуются наличием ограничений и недифференцируемых операторов. Это означает, что традиционные методы анализа, основанные на гладких функциях и линейных уравнениях, часто оказываются неприменимыми. Например, моделирование движения робота с суставами, имеющими пределы угла поворота, требует учета этих ограничений. Аналогично, в экономике, резкие изменения в политике или потребительском поведении приводят к негладким функциям, описывающим динамику системы. Для эффективного анализа таких систем необходимы специальные математические инструменты, такие как вариационное неравенство, негладкий анализ и методы оптимизации с ограничениями. Эти подходы позволяют строить робастные модели, способные адекватно описывать поведение систем в условиях неопределенности и нелинейности, предоставляя ценные сведения для прогнозирования и управления.

Традиционные методы моделирования, основанные на детерминированных уравнениях и аналитических решениях, часто оказываются неэффективными при изучении сложных систем, подверженных стохастическим воздействиям. Неспособность адекватно учитывать случайные флуктуации и нелинейности приводит к значительным отклонениям между теоретическими предсказаниями и наблюдаемыми данными. Особенно остро эта проблема проявляется в системах с большим количеством взаимодействующих элементов, где даже незначительные случайные возмущения могут приводить к качественным изменениям в поведении всей системы. $P(x,t) = \in t K(x,y,t) P(y,t_0) dy$ — уравнение, описывающее эволюцию вероятности, демонстрирует, что точное решение требует знания функции ядра $K$ , которая в сложных системах часто неизвестна или трудновычислима. Таким образом, необходимость разработки новых, более устойчивых к неопределенности и сложности подходов к моделированию становится все более актуальной.

Фундамент Строгости: Определение Решений и Устойчивость

Для моделирования рассматриваемых систем используются стохастические дифференциальные включения (Stochastic Differential Inclusions, SDI). В основе подхода лежит теория максимальных монотонных операторов, позволяющая анализировать и решать такие уравнения. SDI применяются, когда правая часть дифференциального уравнения является не функцией, а многозначным отображением, что отражает неопределенность или множественность возможных эволюций системы. Теория максимальных монотонных операторов предоставляет инструменты для доказательства существования, единственности и устойчивости решений SDI, особенно в контексте нелинейных и нестационарных систем. Формально, SDI описываются уравнением вида $dx(t) \in F(x(t))dt + \sigma(x(t))dW(t)$ , где $F$ — многозначный оператор, σ — оператор диффузии, а $W(t)$ — винеровский процесс.

Для обеспечения корректности (well-posedness) задач, моделируемых стохастическими дифференциальными включениями, необходимо выполнение условия Аттуша-Чарнецкого. Данное условие, выраженное в терминах монотонных операторов, гарантирует существование и единственность решения, а также его устойчивость относительно малых возмущений начальных данных. Формально, условие требует компактности градиента монотонного оператора и ограниченности его роста, что обеспечивает сходимость и предсказуемость поведения системы. Несоблюдение этого условия может привести к непредсказуемым решениям или отсутствию таковых, что делает анализ и контроль системы невозможными. $\partial F(x) : H \rightarrow H$ — оператор, описывающий монотонность, где H — гильбертово пространство.

Определение понятия “сильное решение” в контексте стохастических дифференциальных включений позволяет перейти от простой констатации факта существования решения к анализу его характеристик и свойств. В отличие от “слабых решений”, которые удовлетворяют уравнению лишь в определенном смысле (например, в среднем), сильное решение обладает большей регулярностью и дифференцируемостью. Это позволяет применять к нему стандартные методы анализа, вычислять производные, оценивать скорость сходимости и другие важные параметры. В частности, сильные решения необходимы для построения численных методов решения, обеспечивающих высокую точность и устойчивость, а также для исследования качественных свойств системы, таких как асимптотическое поведение и устойчивость по отношению к возмущениям. Доказательство существования сильного решения часто требует более строгих условий на операторы и начальные данные, чем доказательство существования слабого решения.

Численный Анализ: Аппроксимация Решений во Временном Интервале

Для численного решения стохастических дифференциальных включений, заданных в непрерывном времени, применяется дискретизация по времени. Данный подход заключается в замене непрерывного временного интервала на конечное число дискретных моментов времени $t_i = i\Delta t$ , где $\Delta t$ — шаг дискретизации. В результате, непрерывное дифференциальное включение аппроксимируется рекуррентной последовательностью, определяющей эволюцию решения в дискретные моменты времени. Выбор схемы дискретизации и шага $\Delta t$ оказывает существенное влияние на точность и устойчивость полученного численного решения. Аппроксимация позволяет применять вычислительные методы к задачам, которые невозможно решить аналитически в непрерывном времени.

Скорость сходимости дискретной схемы, используемой для приближения решений стохастического дифференциального включения, является критически важным параметром, определяющим точность полученного численного решения. Более высокая скорость сходимости означает, что при уменьшении шага дискретизации ошибка приближения уменьшается быстрее, что позволяет получить более точные результаты при заданном уровне вычислительных затрат. На практике, скорость сходимости часто выражается порядком сходимости, который указывает, как быстро ошибка уменьшается с уменьшением шага дискретизации $h$ . Оценка скорости сходимости необходима для определения минимального шага $h$ , при котором численное решение будет достаточно точным для поставленной задачи. В противном случае, использование слишком большого шага может привести к значительным погрешностям и неверным выводам.

Анализ демонстрирует сходимость к нулю величин $𝔼[‖Xn-z‖²]$ , $𝔼[λn βn Ψ(Xn)]$ и $𝔼[λn βn ‖\nablaΨ(Xn)‖²]$ при увеличении n, что подтверждает точность разработанной дискретной схемы аппроксимации. При этом, сходимость $𝔼[‖Xn-z‖²]$ указывает на приближение численного решения $Xn$ к истинному решению z, в то время как сходимость $𝔼[λn βn Ψ(Xn)]$ и $𝔼[λn βn ‖\nablaΨ(Xn)‖²]$ обеспечивает сходимость к решению ограничений, заданных функцией Ψ. Достижение этих результатов зависит от выполнения определенных предположений относительно параметров λn, βn и свойств функции Ψ, а также от выбора подходящей дискретизации временного интервала.

Вычислительная Эффективность и Практическое Значение

Анализ сложности по времени выполнения, или FiniteTimeComplexity, продемонстрировал потребность разработанной численной схемы в вычислительных ресурсах. Этот анализ позволяет точно оценить, сколько процессорного времени и памяти потребуется для решения задачи различного масштаба. В частности, установлено, что сложность алгоритма составляет $O(n^k)$ , где $n$ — размер входных данных, а $k$ — константа, зависящая от специфики задачи. Понимание этой зависимости критически важно для определения применимости метода к крупномасштабным проблемам и для оптимизации его реализации с целью минимизации затрат на вычисления и обеспечения эффективного использования доступных ресурсов.

Анализ вычислительной сложности играет ключевую роль в определении применимости разработанного подхода к задачам, характеризующимся большим объемом данных и высокой размерностью. Оценка требуемых вычислительных ресурсов, включая время и память, позволяет установить границы масштабируемости алгоритма и выявить потенциальные узкие места. Без такого анализа невозможно достоверно предсказать, насколько эффективно предложенный метод сможет обрабатывать реальные, крупные массивы данных, что особенно важно для практического применения в различных областях, таких как финансовое моделирование, машинное обучение и оптимизация логистических процессов. В конечном итоге, понимание этих ограничений позволяет исследователям и разработчикам принимать обоснованные решения о целесообразности использования данного подхода и необходимости дальнейшей оптимизации.

Предлагаемый подход представляет собой надежный и эффективный инструмент для решения сложных задач стохастической оптимизации, находящий применение в широком спектре дисциплин. Благодаря своей архитектуре, разработанная система способна эффективно справляться с неопределенностью и шумом, характерными для реальных задач, что делает её особенно ценной в таких областях, как финансовое моделирование, машинное обучение, робототехника и управление ресурсами. В отличие от традиционных методов, данный фреймворк демонстрирует повышенную устойчивость к локальным оптимумам и позволяет находить более качественные решения за разумное время, что подтверждено серией численных экспериментов и сравнительных анализов. Перспективы применения включают оптимизацию портфелей инвестиций, разработку алгоритмов адаптивного управления и повышение эффективности процессов принятия решений в условиях неопределенности.

Усиление Сходимости: Роль Слабой Остроты

Среднее Чезаро представляет собой мощный аналитический инструмент, позволяющий исследовать асимптотическое поведение решений, особенно в случаях, когда традиционные методы оказываются недостаточно эффективными. Данный подход, основанный на усреднении значений траектории решения по времени, обеспечивает сходимость к стабильному состоянию, даже если сама траектория демонстрирует колебания или нестабильность. В частности, среднее Чезаро позволяет оценить долгосрочную тенденцию решения, игнорируя кратковременные флуктуации и обеспечивая более четкое понимание его поведения при $t \rightarrow \in fty$ . Использование среднего Чезаро особенно ценно при анализе итерационных процессов и численных методов, где оценка скорости сходимости играет ключевую роль в определении эффективности алгоритма.

Установлено, что среднее Цезаро траектории сходится к множеству решений со скоростью $O(1/t)$ при определенных условиях. Данный результат демонстрирует, что, несмотря на возможные колебания в краткосрочной перспективе, усредненное поведение траектории приближается к стабильному решению с предсказуемой скоростью убывания ошибки. В частности, скорость сходимости обратно пропорциональна времени, что означает, что чем дольше процесс протекает, тем ближе усредненная траектория к конечному решению. Данное свойство позволяет оценивать и контролировать точность приближения, а также разрабатывать эффективные численные методы для решения сложных задач, где прямая сходимость может быть затруднена.

Исследование показывает, что свойство, названное “слабой остротой” (WeakSharpness) множества решений, играет ключевую роль в обеспечении скорости сходимости усреднённой по Чезаро траектории. $O(1/t)$ — именно такая скорость гарантируется при наличии у множества решений указанного свойства. Слабая острота, по сути, характеризует, насколько «гладким» является множество решений, и чем оно более гладкое, тем быстрее усреднённая траектория приближается к истинному решению. Понимание этой взаимосвязи позволяет не только анализировать поведение численных методов, но и потенциально разрабатывать более эффективные алгоритмы, учитывающие геометрические свойства искомого решения.

Дальнейшие исследования, направленные на изучение связи между понятием Слабой Остроты (WeakSharpness) и эффективностью численных схем, представляются перспективными для повышения их производительности. Установлено, что Слабая Острота решения играет ключевую роль в обеспечении скорости сходимости алгоритмов, и углубленное понимание этой взаимосвязи позволит разрабатывать более оптимальные численные методы. Анализ влияния различных характеристик Слабой Остроты на стабильность и точность схем, а также разработка алгоритмов адаптивной настройки параметров численных методов с учетом этой характеристики, могут значительно улучшить их поведение в сложных вычислительных задачах и обеспечить более быструю и надежную сходимость к решению. Изучение возможности использования Слабой Остроты в качестве критерия остановки итерационных процессов также представляется весьма актуальным.

Исследование, представленное в данной работе, фокусируется на сходимости стохастических методов расщепления для решения обобщенных вариационных неравенств. Подобно тому, как физик стремится понять фундаментальные закономерности, скрытые за кажущимся хаосом, авторы демонстрируют сходимость траекторий в среднем, используя концепцию Cesaro сходимости. Как однажды заметил Альберт Эйнштейн: «Воображение важнее знания. Знание ограничено. Воображение охватывает весь мир». Эта фраза отражает подход, применяемый в статье, где теоретический анализ сочетается с разработкой дискретной по времени численной схемы, позволяющей оценить сложность алгоритма в конечные сроки. Глубокое понимание структуры задачи и умение увидеть взаимосвязи между различными компонентами системы являются ключевыми для успешного решения сложных математических задач.

Куда Далее?

Исследование асимптотического поведения связанных случайных динамических систем, представленное в данной работе, открывает, скорее, поле для новых вопросов, чем дает окончательные ответы. Установленная Cesaro-сходимость траекторий, при всей её элегантности, оставляет открытым вопрос о скорости этой сходимости в более сложных, многомерных пространствах. По сути, демонстрация сходимости — это лишь первый шаг, а истинный вызов заключается в количественном понимании её характера.

Особое внимание заслуживает расширение полученных результатов на случай, когда операторы, определяющие вариационные неравенства, не являются строго монотонными. Введение штрафных методов, безусловно, является полезным инструментом, однако его эффективность напрямую зависит от выбора параметров штрафа, что требует дальнейшего анализа и разработки адаптивных алгоритмов. Нельзя исключать, что истинный прогресс лежит не в усовершенствовании существующих методов, а в поиске принципиально новых подходов к решению этих сложных задач.

В конечном счете, исследование случайных динамических систем — это не просто математическая головоломка, а попытка понять закономерности в хаотичном мире. Подобно тому, как физик ищет фундаментальные законы природы, математик стремится к пониманию общих принципов, управляющих сложными системами. И, возможно, истинная ценность этой работы заключается не в полученных результатах, а в тех вопросах, которые она поднимает.

Оригинал статьи: https://arxiv.org/pdf/2601.15411.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-23 15:22