Синтез стратегий: баланс целей в сложных системах

Автор: Денис Аветисян

В новой работе представлена эффективная методика символического синтеза стратегий, позволяющая учитывать множество требований и находить оптимальные решения в условиях ограниченных ресурсов.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал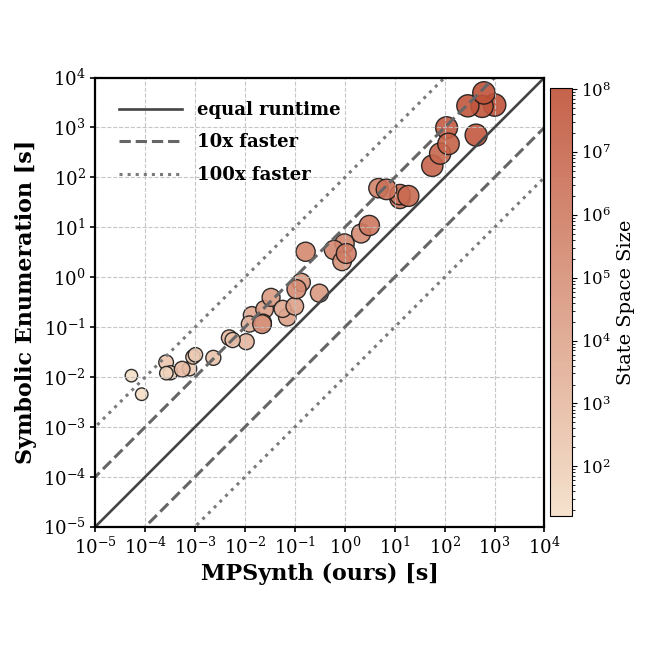

Сравнительный анализ времени работы алгоритма многосвойственного синтеза и базового перечислительного подхода на всех тестовых примерах демонстрирует, что время выполнения варьируется в зависимости от размера пространства состояний, представленного цветовой кодировкой каждой точки данных.

Исследование посвящено синтезу стратегий на основе линейной временной логики над конечными следами (LTLf) с использованием компактного представления достижимых целей и учетом компромиссов между ними.

Не всегда возможно одновременное удовлетворение всех заданных требований к сложной системе. В данной работе, посвященной ‘Multi-Property Synthesis’, исследуется проблема синтеза систем, удовлетворяющих множеству свойств, в условиях, когда полное удовлетворение невозможно. Предложен новый символический алгоритм, компактно представляющий достижимые комбинации целей и синтезирующий стратегии для их реализации, что позволяет эффективно решать задачу компромиссов между свойствами. Какие еще подходы могут быть разработаны для автоматического разрешения конфликтов между требованиями в задачах верификации и синтеза?

Временные Конструкции: Вызов Многоцелевых Задач

Во многих задачах, стоящих перед робототехникой и искусственным интеллектом, требуется одновременное достижение нескольких целей, что представляет собой сложную проблему. В отличие от ситуаций, где необходимо оптимизировать один конкретный параметр, реальные приложения часто требуют баланса между противоречивыми требованиями — например, робот должен быстро переместиться к цели, избегая при этом препятствий и экономя энергию. Эта многоцелевая оптимизация значительно усложняет процесс планирования и управления, поскольку любое решение неизбежно представляет собой компромисс между различными критериями. Эффективное решение подобных задач требует разработки алгоритмов, способных учитывать взаимосвязи между целями и находить оптимальные решения, удовлетворяющие всем требованиям в рамках заданных ограничений.

Традиционные подходы к решению задач, требующих достижения нескольких целей одновременно, зачастую концентрируются на оптимизации лишь одной из них. Это приводит к тому, что итоговое решение может быть далеко от оптимального с точки зрения общей картины, или же, в худшем случае, не учитывать важные аспекты, связанные с другими целями. Например, робот, запрограммированный исключительно на скорость перемещения, может игнорировать препятствия или небрежно обращаться с хрупкими объектами, ставя под угрозу выполнение всей задачи. В результате, несмотря на успешное достижение одной цели, система оказывается неспособной обеспечить комплексное и эффективное решение, что особенно критично в сложных и динамичных средах.

Формальное описание сложных целей в робототехнике и искусственном интеллекте требует создания мощных языков спецификаций, способных точно и недвусмысленно выразить все аспекты задачи. Однако, простого описания недостаточно; необходимы эффективные методы синтеза, позволяющие автоматически генерировать решения, удовлетворяющие всем заданным критериям. Разработка таких методов представляет собой серьезную вычислительную задачу, поскольку пространство возможных решений экспоненциально возрастает с увеличением числа целей и ограничений. Исследователи активно работают над алгоритмами, способными находить оптимальные или, по крайней мере, приемлемые решения в разумные сроки, используя как традиционные методы оптимизации, так и современные подходы машинного обучения, например, обучение с подкреплением, для поиска стратегий, эффективно удовлетворяющих множеству целей одновременно.

Многосвойственный Синтез: Формальный Подход к Целеполаганию

Многосвойственный синтез (Multi-Property Synthesis) предоставляет автоматизированный подход к генерации стратегий, удовлетворяющих набору свойств, сформулированных на языке Линейной Темпоральной Логики над конечными следами (LTLf). В отличие от традиционного синтеза, ориентированного на удовлетворение единственного свойства, данная методология позволяет одновременно учитывать и оптимизировать выполнение нескольких требований. Это достигается путем формального описания желаемого поведения системы в виде набора формул $LTLf$ и последующего поиска стратегии, гарантирующей выполнение всех или максимально возможного числа из них. Результатом является стратегия управления системой, которая обеспечивает корректное поведение с учетом множества заданных критериев.

В основе подхода Multi-Property Synthesis лежит моделирование задачи как игры между агентом и средой, формализованной в виде ‘GameArena’. В рамках этой модели, агент взаимодействует со средой, стремясь выполнить набор заданных свойств, выраженных в логике LTLf. ‘GameArena’ представляет собой формальное описание всех возможных состояний среды и действий агента, а также правил перехода между состояниями. Анализ этой игровой модели позволяет определить, какие свойства могут быть гарантированно выполнены агентом в данной среде, и выработать соответствующую стратегию. Данное представление позволяет применить алгоритмы теории игр для синтеза стратегий, удовлетворяющих заданным требованиям.

В процессе анализа игровой модели, определяемой как ‘GameArena’, выявляется ‘МаксимальноРеализуемоеМножество’ ( $MRS$ ) — наибольшее подмножество заданных свойств LTLf, которое может быть гарантированно выполнено агентом. Определение $MRS$ основывается на поиске такого подмножества, для которого существует стратегия агента, обеспечивающая выполнение всех свойств из этого подмножества при любых действиях среды. Алгоритмы поиска $MRS$ обычно включают в себя итеративное построение и проверку выполнимости стратегий, а также исключение свойств, несовместимых с остальными. Размер $MRS$ служит мерой достижимой степени удовлетворения свойств, а само множество определяет границы возможностей автоматического синтеза стратегий.

Символический Синтез: Абстракция как Инструмент Эффективности

Символический синтез использует такие методы, как бинарные диаграммы решений (BDD), для эффективного представления и манипулирования сложными булевыми выражениями. BDD позволяют компактно кодировать логические функции, представляя их в виде графа, где каждый узел соответствует переменной, а ребра — значениям этой переменной. Это представление позволяет выполнять логические операции над выражениями, такие как конъюнкция, дизъюнкция и инверсия, значительно быстрее, чем при работе с традиционными формами представления булевых выражений. Эффективность BDD обусловлена их способностью обмениваться общими подвыражениями, избегая избыточных вычислений и сокращая требуемый объем памяти. Такой подход особенно полезен при работе с большими и сложными логическими системами, где прямой перебор всех возможных состояний становится вычислительно невозможным.

Метод фиксированной точки (FixedPointComputation) представляет собой итеративный процесс, используемый для определения выигрышных стратегий в игровом пространстве. Он заключается в последовательном приближении к решению путем многократного применения функции перехода, пока не будет достигнута точка, в которой результат итерации перестает меняться. Этот процесс позволяет вычислить оптимальные стратегии для каждого состояния игры, определяя, какие действия приведут к выигрышу при условии оптимальной игры противника. В контексте игровых аренах, фиксированная точка представляет собой состояние, в котором стратегия игрока гарантирует выигрыш или, как минимум, ничью, независимо от действий оппонента. Вычисление фиксированной точки является ключевым шагом в определении оптимальной стратегии игры.

Комбинация двоичных диаграмм принятия решений (BDD) и вычислений неподвижной точки значительно снижает вычислительные затраты на поиск оптимальных стратегий. В ходе тестирования было зафиксировано ускорение работы алгоритмов до двух порядков величины по сравнению с методами, основанными на переборе всех возможных вариантов. Это достигается за счет эффективного представления и манипулирования сложными булевыми выражениями с помощью BDD, что позволяет избежать экспоненциального роста вычислительной сложности, характерного для прямого перебора. Вычисления неподвижной точки, в свою очередь, позволяют итеративно определять выигрышные стратегии, используя компактное представление, полученное с помощью BDD.

Пределы Вычислений и Перспективы Развития

Установлено, что задача мульти-свойственного синтеза относится к классу 2EXPTIME-полных, что определяет теоретические границы её вычислительной сложности. Это означает, что время, необходимое для решения данной задачи, растёт экспоненциально в отношении как количества свойств, так и их сложности, делая поиск оптимального решения чрезвычайно ресурсоёмким при увеличении масштаба. Данный факт накладывает фундаментальные ограничения на возможность построения систем, способных одновременно удовлетворять большому числу сложных требований, и подчёркивает важность разработки эффективных алгоритмов и эвристик для приближённого решения подобных задач. Всё, как и должно быть — системы стареют, вопрос лишь в том, делают ли они это достойно.

Для обеспечения максимальности и полноты поиска, алгоритм использует процедуру, известную как ‘DownwardClosure’. Данный подход систематически исследует все возможные подмножества целевых свойств, начиная с наиболее общих и постепенно уточняя их. По сути, ‘DownwardClosure’ гарантирует, что ни одна комбинация свойств не будет упущена из рассмотрения, что критически важно для нахождения наибольшего набора одновременно удовлетворяемых целей. Алгоритм последовательно проверяет, может ли каждое подмножество свойств быть выполнено, и, если да, добавляет его в итоговый набор, обеспечивая тем самым формальную гарантию полноты и надёжности результата.

Несмотря на установленную теоретическую сложность задачи — 2EXPTIME-полноту — разработанный символьный подход демонстрирует значительное ускорение, достигающее двух порядков величины, по сравнению с методами, основанными на перечислении. Этот прирост производительности не случаен, а обусловлен принципиальным отличием в стратегии поиска. Гарантируя нахождение максимально возможного набора удовлетворяемых целей, данный метод способствует созданию более надёжных и устойчивых систем искусственного интеллекта, способных эффективно решать сложные задачи и адаптироваться к изменяющимся условиям. В отличие от исчерпывающего перебора, символьный подход позволяет систематически исследовать пространство решений, избегая ненужных вычислений и обеспечивая формальную гарантию оптимального результата. И это — не просто алгоритм, а способ сохранить систему в рабочем состоянии, продлить её жизнь в среде постоянных изменений.

Представленное исследование демонстрирует новаторский подход к синтезу систем, удовлетворяющих множеству свойств, особенно в условиях ограниченных ресурсов. Работа затрагивает ключевой аспект — необходимость компромиссов при достижении целей, что неизбежно связано с течением времени и старением любой системы. Как заметил Джон фон Нейман: «В науке не бывает абсолютной истины, только приближения, которые становятся все более точными с течением времени.» Это высказывание особенно применимо к данной работе, поскольку представленный метод позволяет эффективно исследовать пространство возможных решений и находить оптимальные стратегии, учитывая неизбежные ограничения и необходимость адаптации к изменяющимся условиям. По сути, исследование предлагает способ замедлить «старение» системы, продлевая срок ее актуальности и эффективности.

Куда Далее?

Представленный подход к синтезу по множественным свойствам, несомненно, расширяет границы возможного в формальной верификации. Однако, как и любая система, он не свободен от присущих ей ограничений. Компактное представление достижимых множеств целей — это лишь один шаг. Вопрос в том, как эффективно оперировать этими множествами, когда пространство решений становится экспоненциально сложным. Очевидно, что будущие исследования должны сосредоточиться на разработке более изощренных методов аппроксимации и абстракции, чтобы сохранить полезную информацию, отбрасывая избыточность.

Особый интерес представляет изучение динамики trade-offs. Вместо статического анализа, необходимо учитывать, как изменяются приоритеты целей во времени. Какие компромиссы допустимы на ранних стадиях функционирования системы, и какие становятся неприемлемыми с течением времени? По сути, речь идет о создании систем, которые способны к самообучению и адаптации, постоянно пересматривая свои стратегии в ответ на меняющиеся условия.

И, наконец, нельзя забывать о неизбежном: любая система, даже самая тщательно спроектированная, подвержена ошибкам. Следовательно, будущие исследования должны быть направлены не только на предотвращение инцидентов, но и на разработку механизмов быстрого восстановления и адаптации к новым условиям. Ведь инциденты — это не провалы, а шаги системы на пути к зрелости, возможность для самосовершенствования.

Оригинал статьи: https://arxiv.org/pdf/2601.10651.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-17 06:03