Складные конструкции: новый взгляд на кинематику

Автор: Денис Аветисян

В статье представлена унифицированная платформа для анализа движения жестких складных структур, позволяющая моделировать сложные геометрические конфигурации.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал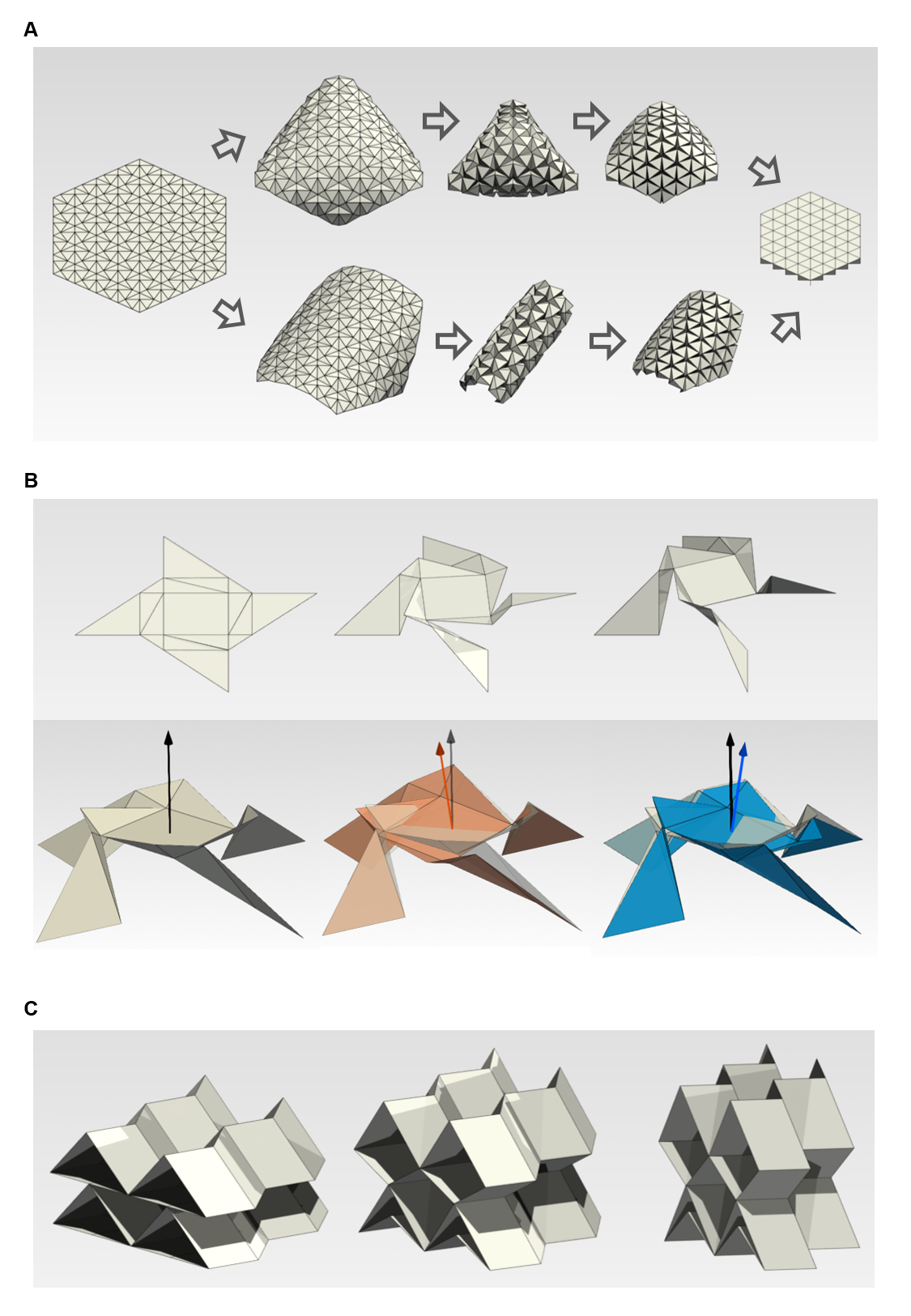

С помощью моделирования складывания изучались различные жестко-оригами структуры: от треугольных решетчатых узоров, демонстрирующих различные траектории складывания, до квадратных механизмов киригами с осесимметричным развертыванием и асимметричными режимами, а также стопкообразных тесселяций Миуры, что позволило выявить принципы управления деформацией в различных конструкциях.

Предложенная методика объединяет графовое представление, теорию винтов и учет кинематических ограничений замкнутых контуров для эффективного моделирования жестких оригами.

Несмотря на растущий интерес к оригами-вдохновленным конструкциям с жесткими элементами, единый подход к анализу их кинематики до сих пор оставался проблемой. В статье ‘A Unified Framework for Kinematic Simulation of Rigid Foldable Structures’ представлен автоматизированный метод, генерирующий матрицу пфаффовых ограничений для произвольных жестких складываемых структур. Разработанный фреймворк объединяет геометрические данные, графовое представление и теорию винтов для обеспечения надежного и масштабируемого моделирования движения. Позволит ли данная методика значительно ускорить проектирование и анализ сложных складываемых конструкций в различных областях техники?

От тонкого листа к устойчивой форме: Новая эра оригами

Традиционное искусство оригами, исторически основанное на использовании тонких и гибких материалов, сталкивается с ограничениями при создании прочных и долговечных конструкций. Именно гибкость позволяет складывать бумагу в сложные формы, но эта же характеристика препятствует использованию оригами в областях, где требуется структурная целостность и устойчивость к внешним воздействиям. В то время как тонкие листы бумаги идеально подходят для создания декоративных моделей или демонстрации математических принципов, их применение в инженерных решениях, например, в создании развертываемых конструкций для космоса или мобильных укрытий, оказывается затруднительным. Данное ограничение стимулирует поиск новых подходов к оригами, позволяющих создавать сложные формы из более прочных и жестких материалов, открывая возможности для применения принципов складывания в областях, где традиционное искусство оригами не может быть реализовано.

Вместо традиционного оригами, использующего тонкие и гибкие материалы, появляется новое направление — “Толстопанельное оригами”, открывающее возможности для создания развертываемых конструкций из жестких элементов. Этот подход позволяет конструировать сложные механизмы и структуры, способные к трансформации и компактному хранению, что особенно важно в таких областях, как космическая техника, робототехника и архитектура. В отличие от классического оригами, где гибкость материала является ключевым фактором, толстопанельное оригами полагается на геометрию и кинематику отдельных жестких панелей, соединенных между собой. Это создает уникальные возможности для разработки саморазворачивающихся конструкций, которые могут быть использованы в ситуациях, требующих быстрого развертывания или адаптации к изменяющимся условиям, например, для создания временных укрытий, развертываемых солнечных батарей или мобильных антенн.

Переход к оригами из толстых панелей, использующих жесткие элементы, требует принципиально нового взгляда на кинематические ограничения, определяющие поведение подобных систем. В отличие от традиционного оригами, где гибкие материалы позволяют легко преодолевать ограничения, жесткие панели накладывают строгие требования на углы поворота и допустимые деформации. Понимание этих ограничений критически важно для проектирования структур, способных к надежному и предсказуемому развертыванию. Необходимо учитывать, как взаимодействие между отдельными панелями влияет на общую кинематическую цепь, и как любые отклонения от идеальной геометрии могут привести к блокировке или повреждению конструкции. Разработка новых математических моделей и алгоритмов анализа становится ключевой задачей для успешной реализации потенциала жесткого оригами в различных областях, от космической техники до архитектуры.

Для полноценной реализации потенциала жесткой оригами необходимы специализированные инструменты анализа кинематического поведения этих структур. Исследователи активно разрабатывают вычислительные модели и алгоритмы, позволяющие предсказывать и оптимизировать процесс складывания и развертывания жестких панелей. Эти инструменты учитывают сложные взаимосвязи между отдельными элементами конструкции, а также ограничения, накладываемые геометрией и материалами. Точный анализ позволяет выявлять оптимальные конфигурации, минимизировать напряжения и обеспечить надежное функционирование развертываемых конструкций, открывая путь к созданию прочных и функциональных устройств, использующих принципы жесткой оригами в различных областях — от космической техники до робототехники и архитектуры.

Соединение фасеток методом пайки позволяет создавать тесселяции TMP, а изменение положения петель обеспечивает реализацию толстостенных панелей по узорам Миуры и Ёсимуры.

От структуры к графу: Формализация движения

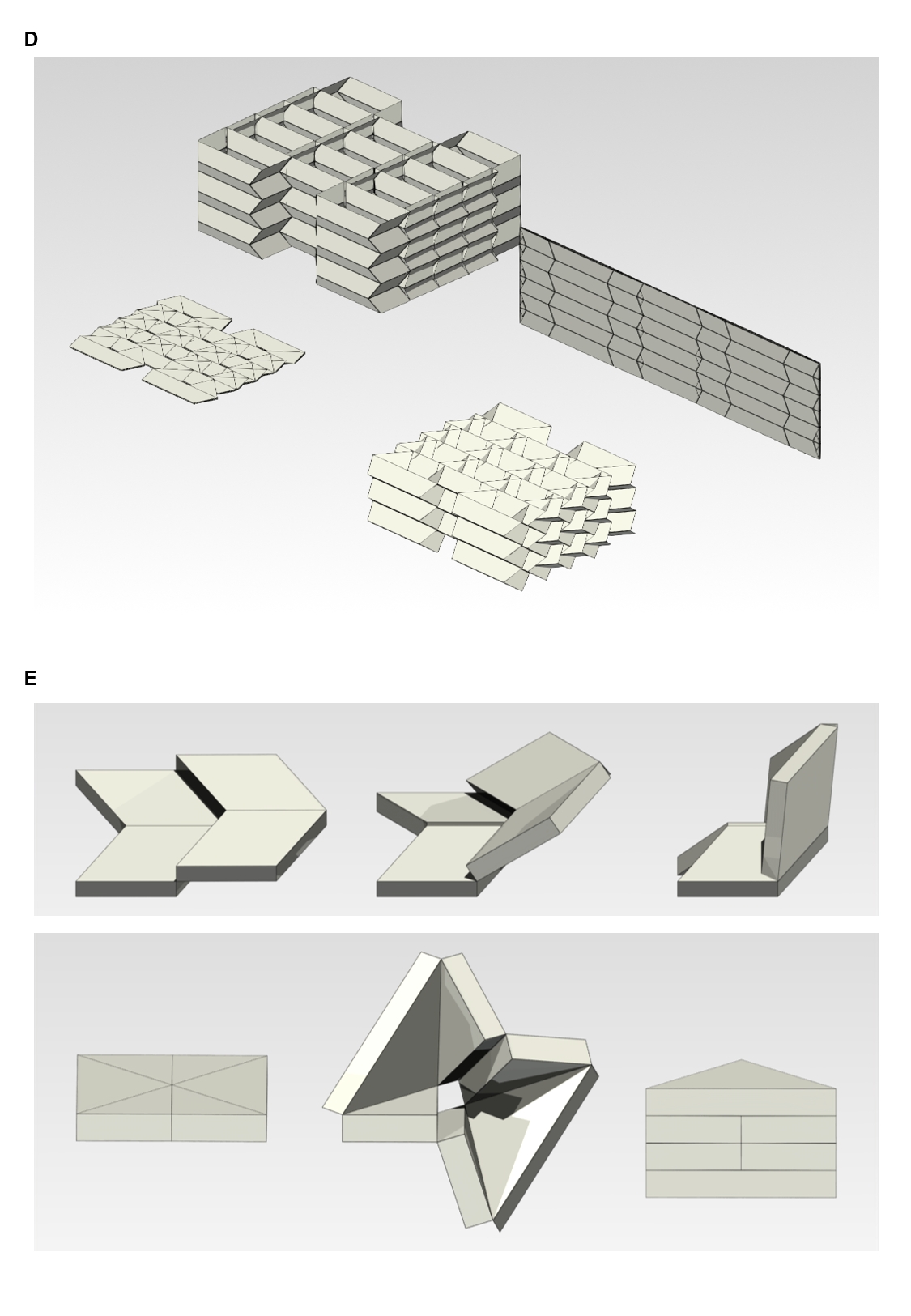
Схема данных представляет собой структурированное описание геометрических параметров и связности жесткой складывающейся конструкции. Эта схема включает в себя информацию о расположении и размерах граней (facets), а также о типах и расположении шарниров (hinges), соединяющих эти грани. Каждая грань описывается своими координатами в пространстве, размерами и материальными свойствами. Шарниры определяются типом соединения (например, вращательным или поступательным) и ограничивают возможные движения между соединенными гранями. Такая структурированная организация данных позволяет однозначно определить геометрию и кинематическую связь всех элементов конструкции, что является необходимым условием для последующего анализа и моделирования её поведения.

Геометрические данные и связи жесткой складывающейся структуры преобразуются в ‘Граф граней-петлей’, где каждая грань структуры представлена как узел графа, а каждая петля (шарнирное соединение) — как ребро. Такое представление позволяет формализовать структуру как математический граф, где узлы соответствуют плоским поверхностям, а ребра — осям вращения между ними. Каждый узел имеет атрибуты, описывающие его геометрию, а каждое ребро — характеристики петли, включая тип соединения и ограничения на движение. В результате получается дискретная модель, пригодная для алгоритмического анализа кинематических свойств структуры.

Представление структуры в виде графа позволяет применить методы теории графов для выявления и анализа кинематических ограничений. Каждая плоскость (фасет) структуры моделируется как узел графа, а шарнирное соединение между плоскостями — как ребро. Это преобразование позволяет формализовать связи между элементами структуры и использовать такие инструменты теории графов, как матрицы инцидентности и смежности, для определения степеней свободы и зависимостей между углами вращения плоскостей. Идентифицированные циклы в графе соответствуют кинематическим цепям, а анализ этих цепей позволяет определить, какие движения возможны или запрещены для данной структуры, и, следовательно, выявить её кинематические ограничения.

Преобразование структуры в графовое представление является основой для проведения строгой кинематической оценки. Графовая модель, где грани структуры выступают в роли узлов, а шарниры — в роли ребер, позволяет формализовать анализ степеней свободы и ограничений, действующих на механизм. Использование методов теории графов, таких как поиск циклов и определение связности, позволяет выявлять критические кинематические цепи и потенциальные ограничения движения. Это, в свою очередь, обеспечивает возможность построения точной математической модели, необходимой для дальнейшего расчета и оптимизации кинематических характеристик механизма и позволяет проводить анализ устойчивости и работоспособности конструкции.

Предложенная схема данных позволяет представить соединения в листах, такие как шарнирные в ячейках сложенного оригами Миуры (SMO), добавляющие ребра в граф, или паяные в ячейках полиэдра Тати-Миуры (TMP), объединяющие узлы и формируя различные графовые представления.

Уточнение ограничений: Циклы и матрицы

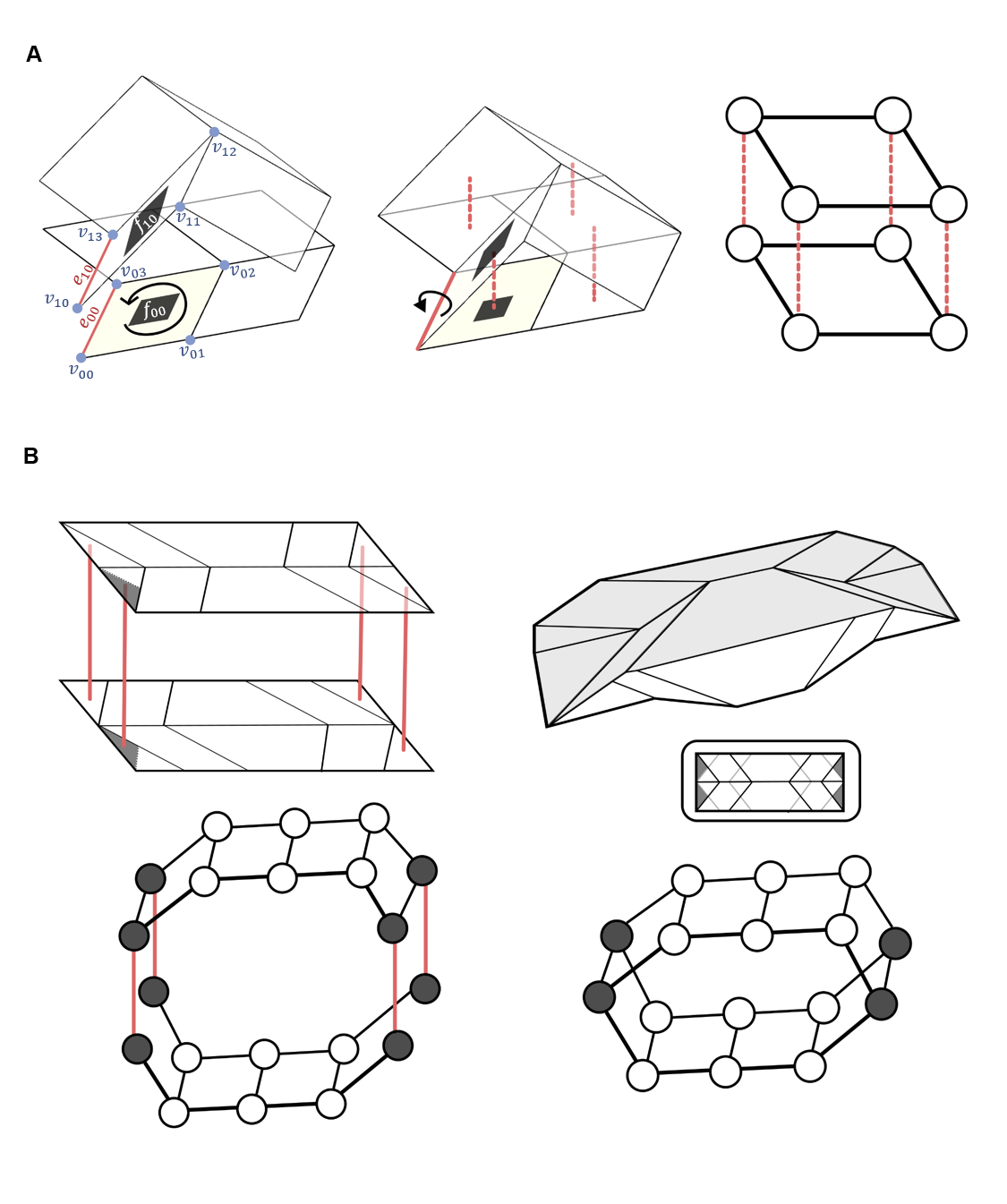
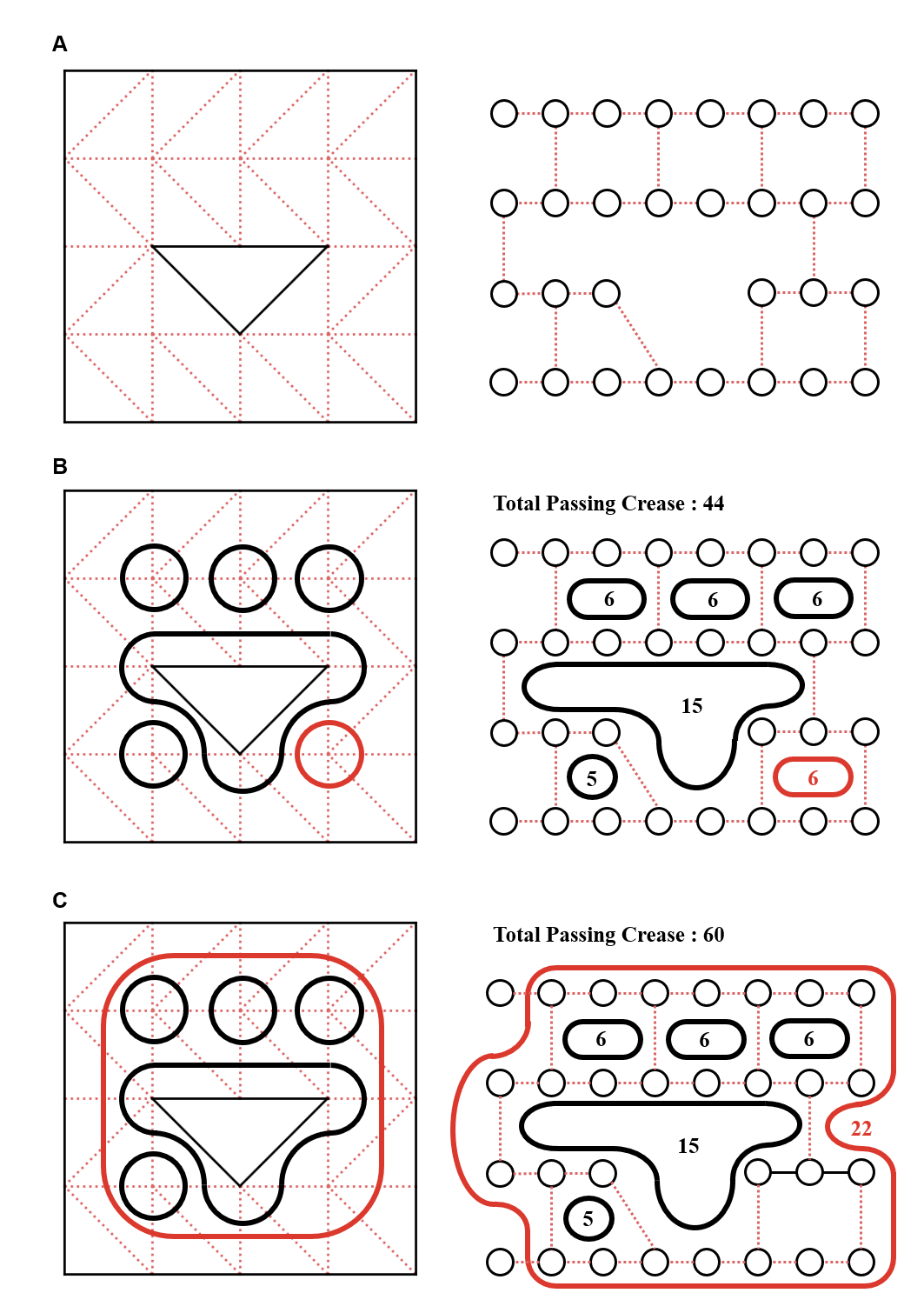
Ограничения замыкания контура (Loop Closure Constraints) возникают в графе фасет-петли (facet-hinge graph) при наличии замкнутых циклов, образованных последовательностью сочленений и граней. Эти циклы накладывают ограничения на допустимые перемещения механизма, поскольку любое движение, нарушающее замкнутость цикла, является кинематически невозможным. Фактически, каждое замкнутое кольцо в графе представляет собой уравнение, связывающее углы поворота сочленений и линейные перемещения граней, определяющее совместимую конфигурацию механизма. Таким образом, анализ ограничений замыкания контура критически важен для обеспечения корректной работы и предотвращения перенапряжений в механических системах.

Минимальная циклическая база (Minimum Cycle Basis, МЦБ) представляет собой подмножество всех возможных циклов в графе шарнирно-гранном соединения, отобранное таким образом, чтобы оно было минимальным и линейно независимым. Это означает, что каждый цикл в МЦБ содержит информацию, отсутствующую в других циклах, и что ни один цикл в базе не может быть получен как линейная комбинация других циклов. Использование МЦБ существенно упрощает анализ кинематических ограничений, поскольку позволяет оперировать лишь небольшим набором независимых уравнений вместо рассмотрения всех возможных циклов, что значительно снижает вычислительную сложность и позволяет эффективно представлять и решать задачи кинематики.

Матрица Пфаффа — это математическое представление кинематических связей, возникающих из замкнутых контуров в графе шарнирно-гранного механизма. Она формируется на основе векторов обобщенных координат и скоростей, отражая ограничения на движение механизма. Каждая строка матрицы соответствует одному замкнутому контуру и представляет собой линейную комбинацию скоростей обобщенных координат, равную нулю. Таким образом, матрица Пфаффа позволяет численно выразить условия неразрывности механизма и служит основой для решения задач кинематического анализа и синтеза. Размерность матрицы определяется количеством степеней свободы механизма и количеством независимых замкнутых контуров.

Теория винтов (Screw Theory) служит геометрической основой для вывода кинематических ограничений, обеспечивая их точность. В рамках этой теории, любое бесконечно малое перемещение твердого тела может быть представлено как винтовое движение, характеризующееся линейной скоростью и угловой скоростью вокруг оси. Эти скорости формируют шестимерный вектор $\mathbb{V}$ , представляющий собой пространство винтов. Кинематические ограничения, возникающие из-за связей между звеньями механизма, выражаются в виде линейных уравнений, ограничивающих этот вектор $\mathbb{V}$ . Использование теории винтов гарантирует, что эти уравнения точно отражают геометрические взаимосвязи, избегая избыточности и обеспечивая корректное решение задач кинематического анализа и синтеза.

Существуют однозначное соответствие между замкнутыми контурами в узорах и циклами в графах, что демонстрируется на примере жестко складывающегося киригами, где минимальный базис циклов определяет полный и минимальный набор контуров, в отличие от избыточного набора, содержащего излишние циклы.

Раскрытие пространства возможностей: Паттерны и применения

Разнообразие возможных конфигураций складывания демонстрируется такими узорами, как паттерн Реша и паттерн Ёсимуры. Эти геометрические построения, кажущиеся на первый взгляд абстрактными, на самом деле представляют собой фундаментальные принципы, лежащие в основе оригами и других складных структур. Паттерн Реша, характеризующийся специфической последовательностью сгибов, позволяет создавать сложные трехмерные формы из плоских листов материала. В то же время, паттерн Ёсимуры, основанный на использовании “лепестков”, обеспечивает возможность создания более плавных и органичных форм. Изучение этих и других подобных узоров открывает новые горизонты в разработке инновационных складных конструкций, способных адаптироваться к различным условиям и выполнять широкий спектр функций.

Кинематический анализ, основанный на разработанных инструментах, предоставляет возможность прогнозировать поведение при складывании и структурную устойчивость оригами. Этот подход позволяет исследователям и инженерам предвидеть, как конкретная конструкция будет деформироваться и реагировать на нагрузки в процессе складывания и разворачивания. Используя математические модели и алгоритмы, можно оценить напряжения, деформации и критические точки конструкции, что особенно важно при проектировании сложных механизмов и структур. По сути, кинематический анализ выступает в роли виртуального прототипа, позволяя оптимизировать конструкцию до физического создания, тем самым значительно снижая риски и затраты, а также обеспечивая надежность и долговечность будущих устройств и сооружений.

Метод смещения петель, или ‘Hinge Shifting’, представляет собой инновационный подход к управлению процессом складывания в оригами из толстых панелей. В отличие от традиционных техник, где фиксированные петли ограничивают возможности трансформации, данная методика позволяет точно контролировать движение каждой панели. Это достигается за счет стратегического изменения положения петель во время складывания, что позволяет создавать сложные геометрические формы и оптимизировать процесс деформации материала. Благодаря этой технике становится возможным не только предсказуемое и контролируемое складывание, но и повышение структурной устойчивости готового изделия, открывая перспективы для создания адаптивных конструкций в архитектуре и космосе.

Разработанная методология открывает широкие перспективы для создания инновационных конструкций в различных областях. От развертываемых космических аппаратов, требующих компактности при транспортировке и надежности в условиях вакуума, до адаптивных архитектурных элементов, способных изменять свою форму и функциональность в зависимости от внешних условий и потребностей, — возможности применения практически безграничны. Технологии, позволяющие точно контролировать процесс складывания и обеспечивать структурную устойчивость, позволяют создавать сложные механизмы, применимые в робототехнике, медицине и других областях, где требуется компактность, надежность и возможность трансформации.

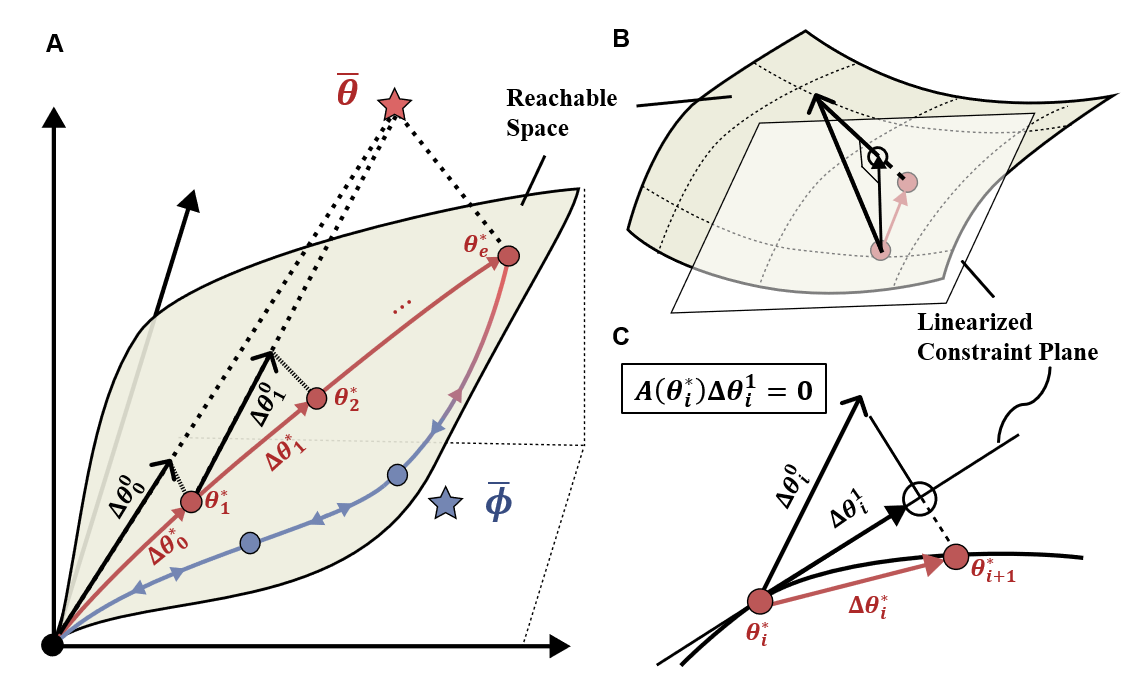
Вычисление допустимой траектории складывания на основе матрицы ограничений включает в себя проектирование энергетических изменений в пространстве переменных на плоскость ограничений с последующей коррекцией методом Ньютона-Рафсона для достижения следующей допустимой конфигурации.

Представленная работа демонстрирует стремление к элегантности в решении сложных задач кинематического моделирования жестких складываемых структур. Анализ, основанный на интеграции графового представления, теории винтов и ограничений замкнутых контуров, позволяет достичь масштабируемости и надежности симуляций. Это соответствует убеждению, что истинное понимание проявляется в способности упростить сложное. Как однажды заметила Грейс Хоппер: «Лучший способ предсказать будущее — создать его». Эта фраза отражает суть подхода, представленного в статье: не просто описывать кинематику, а активно формировать возможности для создания новых, сложных механизмов и структур, основываясь на четком и лаконичном математическом аппарате.

Что дальше?

Представленная работа, хотя и стремится к объединению методов анализа жестких складываемых структур, лишь обнажает сложность вопроса. Система, требующая столь обширного инструментария для описания, кажется, признает собственную громоздкость. Успех не в количестве поддерживаемых конфигураций, а в способности обходиться без них. Стремление к универсальности часто оборачивается утяжелением, а понятность — вежливостью, которую не всегда хватает.

Основным узким местом остается масштабируемость. Текущий подход, хотя и эффективен для демонстрационных моделей, сталкивается с трудностями при анализе структур с большим числом звеньев и кинематических петель. Следующим шагом представляется не усложнение алгоритмов, а поиск принципиально новых подходов, возможно, основанных на упрощении геометрической модели или использовании методов, заимствованных из теории графов и комбинаторики.

В конечном счете, истинная ценность подобных исследований не в создании еще одного инструмента для симуляции, а в углублении понимания фундаментальных принципов, управляющих складными структурами. Идеальная модель — это не та, которая воспроизводит реальность, а та, которая позволяет предсказать ее, не нуждаясь в самой реальности.

Оригинал статьи: https://arxiv.org/pdf/2601.10225.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-17 09:27