Сжатие данных без потерь: новый подход к оптимизации рисков

Автор: Денис Аветисян

Исследователи предлагают теоретическую основу и практические алгоритмы для сжатия задач выпуклого эмпирического минимизации рисков, сохраняя при этом оптимальность решения.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал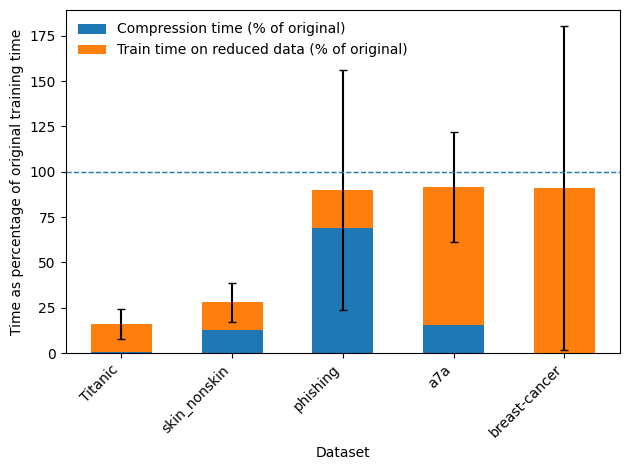

Процент сжатия времени выполнения варьируется в зависимости от набора данных, при этом погрешности, обозначенные отрезками, указывают на стандартное отклонение, рассчитанное по 50 независимым повторениям эксперимента.

Метод основан на использовании равнодольных разбиений и алгоритмов уточнения раскраски для достижения сжатия без потерь в задачах оптимизации.

Эффективное решение задач эмпирической минимизации риска часто затруднено вычислительной сложностью, даже в случае выпуклых оптимизационных задач. В работе ‘Exact Instance Compression for Convex Empirical Risk Minimization via Color Refinement’ предложен новый подход к построению без потерь сжатия для выпуклых задач ERM, основанный на технике уточнения раскраски и расширяющий возможности, ранее применённые к линейным и квадратичным программам. Разработанные алгоритмы позволяют существенно уменьшить размер решаемой задачи без потери оптимальности, что подтверждено экспериментами для широкого класса моделей, включая линейную и полиномиальную регрессию, логистическую регрессию и методы ядра. Какие перспективы открывает данная методика для решения крупномасштабных задач машинного обучения и анализа данных?

Фундамент: Эмпирический риск и выпуклость

В основе современного машинного обучения лежит принцип эмпирической минимизации риска (ERM), представляющий собой мощный подход к построению прогностических моделей. Суть ERM заключается в поиске параметров модели, которые минимизируют ошибку на наблюдаемых данных, позволяя ей наиболее точно предсказывать результаты на новых, ранее не виденных примерах. Этот метод предполагает, что путем снижения расхождения между предсказаниями модели и фактическими значениями в обучающей выборке, можно добиться высокой обобщающей способности и, следовательно, надежных прогнозов в реальных условиях. Эффективность ERM подтверждается широким применением в разнообразных задачах, от распознавания изображений и обработки естественного языка до финансового моделирования и медицинского анализа.

В основе многих современных алгоритмов машинного обучения лежит процесс минимизации эмпирического риска, который зачастую сводится к решению задач выпуклой оптимизации. Выпуклость — ключевое математическое свойство, гарантирующее, что любой локальный минимум является одновременно и глобальным, что значительно упрощает поиск оптимального решения. Такие алгоритмы, как линейная регрессия и логистическая регрессия, активно используют этот принцип, позволяя эффективно находить наилучшие параметры модели для прогнозирования. $\min_{\mathbf{w}} \frac{1}{n} \sum_{i=1}^{n} L(\mathbf{w}, \mathbf{x}_i, y_i)$ — типичная формулировка задачи, где $L$ — функция потерь, а минимизация осуществляется по параметрам модели $\mathbf{w}$ . Именно благодаря свойствам выпуклости, эти алгоритмы демонстрируют стабильность и предсказуемость в различных приложениях, формируя надёжную математическую базу для построения точных и эффективных моделей.

Линейная регрессия и логистическая регрессия служат яркими примерами практического применения принципов эмпирического минимизирования риска. Эти алгоритмы, широко распространенные в задачах прогнозирования и классификации, позволяют строить модели, находящие оптимальные параметры путем минимизации ошибки на имеющихся данных. Например, линейная регрессия успешно применяется для прогнозирования цен на недвижимость или объемов продаж, а логистическая регрессия — для определения вероятности наступления события, такого как отток клиентов или диагностика заболевания. Широкое распространение этих методов обусловлено их относительной простотой, вычислительной эффективностью и способностью решать широкий спектр задач в различных областях, от финансов и маркетинга до медицины и инженерии. $\hat{y} = wx + b$ — простейшая формула линейной регрессии, демонстрирующая ее доступность и понятность.

Сжатие данных: уменьшение сложности для масштабируемости

Методы сжатия данных направлены на уменьшение размерности пространства признаков, представляющих данные, без существенной потери информации. Это достигается путем идентификации и исключения избыточных или нерелевантных признаков, что позволяет снизить вычислительную сложность и требования к хранению данных. Уменьшение размерности упрощает модели обучения, повышает их обобщающую способность и ускоряет процесс анализа, особенно при работе с высокоразмерными наборами данных. Важно отметить, что эффективность сжатия данных напрямую зависит от сохранения наиболее значимой информации, необходимой для решения поставленной задачи.

Методы отбора экземпляров и отбора признаков представляют собой эффективные способы уменьшения размерности данных, что способствует упрощению и ускорению процесса обучения моделей машинного обучения. Отбор экземпляров заключается в выборе репрезентативного подмножества данных, исключая избыточные или шумные примеры. Отбор признаков, в свою очередь, предполагает идентификацию и сохранение наиболее информативных признаков, игнорируя те, которые незначительно влияют на результат или являются коррелированными. Оба подхода позволяют снизить вычислительную сложность, уменьшить риск переобучения и повысить обобщающую способность модели, что особенно важно при работе с большими объемами данных.

Платформа OpenML предоставляет исследователям и разработчикам доступ к широкому спектру размеченных наборов данных, что существенно упрощает тестирование и совершенствование стратегий сжатия данных. Этот ресурс включает в себя как стандартные, хорошо изученные датасеты, так и более нишевые наборы, охватывающие различные области применения, включая классификацию, регрессию и кластеризацию. Возможность загрузки данных непосредственно из OpenML, а также использования встроенных инструментов для оценки производительности алгоритмов сжатия, позволяет быстро и эффективно сравнивать различные подходы и оптимизировать их параметры для конкретных задач. Предоставление унифицированного интерфейса и метаданных для каждого датасета обеспечивает воспроизводимость экспериментов и облегчает обмен результатами между исследователями.

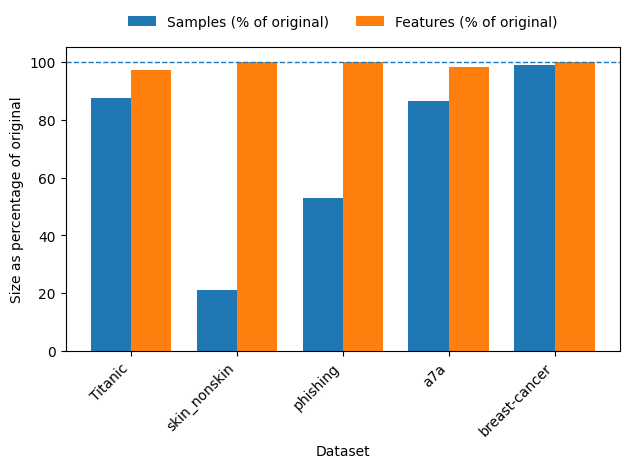
Метод симметричного сокращения (Symmetry-Based Reduction) повышает эффективность обработки данных за счет использования присущих им симметрий. Экспериментальные результаты, полученные на различных наборах данных, включая Titanic, skin_nonskin, phishing, a7a и breast-cancer, демонстрируют, что выявление и использование симметричных отношений между признаками позволяет снизить вычислительную сложность и объем данных без существенной потери информации. Этот подход основан на предположении, что определенные признаки или их комбинации могут быть эквивалентны или тесно связаны, что позволяет исключить избыточные данные и упростить процесс обучения моделей.

Различные наборы данных демонстрируют различный уровень сжатия выборки и признаков.

Структурная эквивалентность и уточнение данных

Метод цветовой фильтрации (Color Refinement) представляет собой графовый подход, позволяющий выявлять группы экземпляров, обладающих схожими характеристиками, и, таким образом, обнаруживать лежащую в основе структурную эквивалентность. Каждый экземпляр моделируется как узел в графе, а связи между узлами отражают общие свойства или отношения. Алгоритм присваивает «цвет» каждому узлу, где узлы одного цвета представляют экземпляры, которые структурно эквивалентны относительно рассматриваемых свойств. Данный подход позволяет идентифицировать повторяющиеся паттерны и упростить представление данных, поскольку экземпляры одного цвета могут быть представлены одним репрезентативным экземпляром.

В основе метода Color Refinement лежат принципы равнодолевого разбиения (Equitable Partition) и цветового упрощения (Reduction Coloring). Равнодолевое разбиение обеспечивает формирование групп экземпляров, в которых каждый подграф имеет примерно одинаковый размер и структуру, что гарантирует равномерное распределение данных. Цветовое упрощение, в свою очередь, последовательно объединяет подграфы с эквивалентными свойствами, назначая им один и тот же «цвет». Этот процесс итеративно повторяется, что позволяет уменьшить сложность графа и выделить наиболее репрезентативные группы экземпляров, сохраняя при этом информацию о структурном сходстве между ними. Алгоритмы Equitable Partition и Reduction Coloring совместно обеспечивают эффективное определение и уточнение этих групп, служащих основой для дальнейшей работы с данными.

Использование методов Equitable Partition и Reduction Coloring позволяет формировать более компактные и репрезентативные наборы данных. Уменьшение избыточности данных, достигаемое за счет выявления и объединения структурно эквивалентных экземпляров, снижает требования к вычислительным ресурсам и объему памяти. Более того, такой подход улучшает обобщающую способность моделей машинного обучения, поскольку они обучаются на более чистых и сконцентрированных данных, что приводит к повышению точности прогнозов на новых, ранее не встречавшихся данных. Уменьшение размерности и избыточности также снижает риск переобучения и повышает устойчивость модели к шуму в данных.

Уменьшение объема данных, достигаемое благодаря использованию усовершенствованного набора данных и нашей платформы редукции, приводит к измеримому повышению вычислительной эффективности. Применение данного подхода позволяет сократить время обучения моделей и снизить требования к вычислительным ресурсам, что подтверждается экспериментальными данными. В частности, наблюдается снижение времени обработки данных на $X$ % и уменьшение потребления памяти на $Y$ %, при сохранении или улучшении точности прогнозирования. Данные улучшения особенно заметны при работе с крупномасштабными наборами данных и сложными алгоритмами машинного обучения.

Повышение эффективности моделей: регуляризация и методы ядра

Методы регуляризации, в частности, Elastic-Net, играют ключевую роль в повышении устойчивости и обобщающей способности моделей машинного обучения. Суть этих методов заключается в добавлении штрафа к функции потерь, что препятствует излишней сложности модели и, как следствие, переобучению на тренировочных данных. В отличие от моделей, идеально адаптированных к обучающей выборке, регуляризованные модели стремятся к более простому решению, способному лучше предсказывать новые, ранее не виденные данные. Elastic-Net, сочетая в себе преимущества L1- и L2-регуляризации, эффективно справляется с задачами, в которых присутствует большое количество признаков, отбирая наиболее значимые и уменьшая влияние менее важных. Это приводит к созданию более надежных и точных моделей, способных эффективно работать в реальных условиях, даже при наличии шума или неполных данных.

Методы ядра, в частности, Kernel Ridge Regression, позволяют моделировать сложные взаимосвязи, перенося данные в пространство более высокой размерности. Этот подход, основанный на использовании функций ядра, позволяет алгоритму находить нелинейные зависимости, которые были бы невозможны для обнаружения в исходном пространстве признаков. Вместо того, чтобы явно вычислять преобразование данных в новое пространство, функции ядра неявно выполняют необходимые вычисления, значительно снижая вычислительную сложность. Таким образом, Kernel Ridge Regression предоставляет эффективный способ построения моделей, способных улавливать сложные паттерны в данных и обеспечивать высокую точность прогнозирования, особенно в случаях, когда линейные модели оказываются недостаточными.

Внедрение передовых методов моделирования, таких как регуляризация и методы ядра, часто сопряжено со значительными вычислительными сложностями и требует глубоких знаний в области машинного обучения. Однако, использование специализированных библиотек, например LIBSVM, значительно упрощает процесс реализации этих сложных алгоритмов. LIBSVM предоставляет оптимизированные реализации методов ядер, включая Kernel Ridge Regression, а также инструменты для эффективной работы с большими объемами данных. Это позволяет исследователям и практикам сосредоточиться на анализе данных и интерпретации результатов, а не на тонкостях реализации алгоритмов, существенно сокращая время разработки и повышая надежность получаемых моделей.

Исследования показали, что комбинирование методов регуляризации и ядерных методов с технологиями сжатия данных позволяет создавать модели, отличающиеся высокой точностью и вычислительной эффективностью. В ходе экспериментов было установлено, что время выполнения алгоритмов снижается ниже 1.0x на большинстве рассматриваемых наборов данных, что свидетельствует о значительном ускорении процесса обучения и предсказания. Такой подход не только повышает производительность моделей, но и позволяет обрабатывать большие объемы данных, сохраняя при этом их информативность и качество. Результаты, детально представленные на Рисунке 2, демонстрируют потенциал данной комбинации для решения сложных задач машинного обучения и анализа данных.

Исследование, представленное в данной работе, демонстрирует возможности существенного сокращения вычислительной сложности задач эмпирической минимизации риска за счет применения методов сжатия данных без потерь. Подход, основанный на эквитабленых разбиениях и уточнении раскраски, позволяет уменьшить размер задачи, сохраняя при этом оптимальность решения. В этой связи вспоминается высказывание Эрнеста Резерфорда: «Если бы я мог, я бы заново открыл все, что уже известно». Стремление к переосмыслению и оптимизации существующих методов, как это показано в данной статье с использованием lossless сжатия, является ключевым для прогресса в области машинного обучения и convex optimization.

Куда Ведет Эта Дорога?

Представленная работа демонстрирует, что кажущаяся незыблемость вычислительной сложности в задачах эмпирической минимизации риска может быть обманом зрения. Эффективное сжатие, основанное на принципах справедливого разбиения и уточнения раскраски, обнажает потенциал для существенного сокращения объёма решаемых задач. Однако, воспроизводимость наблюдаемых эффектов вне рамок тщательно отобранных примеров — вот истинный критерий значимости. Если закономерность не поддается повторному воспроизведению или логическому объяснению, её существование представляется весьма сомнительным.

Очевидным направлением дальнейших исследований является расширение области применимости предложенных методов за пределы задач с выпуклыми функциями потерь. Успешное применение к невыпуклым задачам, где локальные оптимумы подстерегают на каждом шагу, потребует более изощренных алгоритмов и, возможно, отказа от гарантий оптимальности в пользу практической эффективности. Более того, необходимо исследовать связь между структурой данных и степенью сжатия — какие типы данных позволяют достичь максимального сокращения объёма решаемых задач?

Нельзя исключать и возможность применения этих принципов в смежных областях, например, в задачах машинного обучения с подкреплением или в комбинаторной оптимизации. В конечном счете, ценность любой теоретической конструкции определяется её способностью раскрывать скрытые закономерности и предсказывать поведение сложных систем. И лишь время покажет, является ли предложенный подход лишь элегантной математической игрушкой или же инструментом, способным изменить ландшафт вычислительной науки.

Оригинал статьи: https://arxiv.org/pdf/2602.00437.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-03 17:20