Торги в Сети: Новые Границы Эффективности

Автор: Денис Аветисян

Исследование предлагает новые алгоритмы для онлайн-торговли, позволяющие максимизировать прибыль в условиях неопределенности и ограниченной обратной связи.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал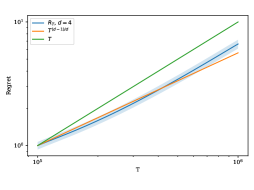

Среднее сожаление, представленное на рисунке, демонстрирует соответствие полученных результатов теоретическим границам, что подтверждает обоснованность предложенного подхода.

Работа устанавливает строгие границы сожаления для онлайн-двусторонней торговли с использованием непараметрических контекстуальных бандитов и однобитной обратной связи, достигая скорости O(T^(d-1)/d).

В задачах онлайн-торговли, как правило, предполагается знание ценности товара для покупателя и продавца, что часто нереалистично. В данной работе, посвященной проблеме ‘Nonparametric Contextual Online Bilateral Trade’, исследуется сценарий, в котором участники торгов не раскрывают свои оценки, а алгоритм должен предлагать цену, учитывая контекстную информацию. Мы получаем гарантированную оценку сожаления $\widetilde{O}(T^{{(d-1)}/d})$ для алгоритма, работающего с однобитной обратной связью и строгим бюджетным балансом. Возможно ли дальнейшее улучшение границ сожаления в условиях ограниченной информации и строгих бюджетных ограничений?

Вызов Онлайн-Торговли: Адаптация к Неизвестности

Базовая задача двусторонней торговли моделирует фундаментальные экономические обмены, однако её онлайн-вариант представляет собой значительные трудности в плане обучения. В классической модели участники торговли обладают полной информацией о предпочтениях друг друга, что позволяет им быстро достигать оптимальных соглашений. В онлайн-среде, напротив, агенты взаимодействуют с новыми контрагентами, не зная их ценностей и предпочтений. Это требует разработки алгоритмов, способных адаптироваться к неизвестным оценкам и эффективно учиться на каждом взаимодействии. Сложность заключается в том, что алгоритм должен не только максимизировать текущую прибыль, но и минимизировать кумуляльное сожаление — разницу между его результатами и оптимальной стратегией — на протяжении всех транзакций. Такая адаптивность представляет собой серьезный вызов для современных алгоритмов машинного обучения и требует инновационных подходов к решению проблемы онлайн-торговли.

В задаче онлайн-торговли между двумя сторонами агент последовательно взаимодействует с новыми покупателями и продавцами, что требует от алгоритмов быстрой адаптации к неизвестным ценовым предпочтениям. Каждое новое взаимодействие представляет собой уникальную ситуацию, поскольку истинные оценки покупателей и продавцов остаются скрытыми. Таким образом, алгоритм должен уметь эффективно оценивать эти скрытые факторы на основе ограниченной информации, полученной в процессе торговли. Успешная адаптация к этим меняющимся условиям критически важна для максимизации прибыли или достижения оптимального результата в долгосрочной перспективе, поскольку статические стратегии оказываются неэффективными в динамичной среде онлайн-торговли. Алгоритмы, способные к быстрому обучению и адаптации, позволяют агенту оперативно реагировать на изменения в рыночной конъюнктуре и поддерживать конкурентоспособность.

Успешное функционирование в условиях онлайн-торговли требует минимизации кумулятивного сожаления — разницы между результатами работы алгоритма и оптимальной стратегией на протяжении всех взаимодействий. Достижение этой цели представляется сложной задачей из-за внутренней сложности самой проблемы. Алгоритм должен оперативно адаптироваться к неизвестным предпочтениям участников, постоянно оценивая и корректируя свою тактику, чтобы избежать значительных потерь в сравнении с идеальным решением. В условиях непрерывного потока новых контрагентов, где каждая сделка представляет собой уникальный эксперимент, построение алгоритма, способного к эффективному обучению и минимизации общего сожаления, является ключевой задачей для обеспечения стабильности и прибыльности в динамичной среде онлайн-торговли. $\text{Cumulative Regret} = \sum_{t=1}^{T} (V_t - A_t)$ , где $V_t$ — оптимальная прибыль в момент времени t, а $A_t$ — прибыль, полученная алгоритмом.

Иерархический Подход к Оценке

В основе нашего подхода лежит древовидная структура, предназначенная для иерархического разделения пространства возможных оценок. Данная структура позволяет алгоритму последовательно сужать область поиска оптимальной цены, разделяя пространство оценок на подпространства. Каждая ветвь дерева представляет собой определенный диапазон значений, что обеспечивает более целенаправленное исследование и повышает эффективность процесса обучения. Использование иерархического разбиения позволяет алгоритму быстро фокусироваться на наиболее перспективных областях пространства оценок, значительно сокращая время, необходимое для достижения конвергенции и повышения точности.

В рамках иерархической структуры оценки используется процедура “Предложение цены” (Guess Routine) для формирования начальных оценок стоимости, и процедура “Уточнение оценки” (Reduce Routine) для итеративной корректировки этих оценок на основе результатов сделок. Процедура “Предложение цены” генерирует стоимость актива, а процедура “Уточнение оценки” анализирует результат сделки — принятие или отклонение предложения — и соответствующим образом корректирует оценку. Этот итеративный процесс позволяет алгоритму быстро сходиться к более точным значениям, даже при ограниченном количестве обратной связи от торговых операций.

Алгоритм оценки, использующий иерархическую структуру, спроектирован для эффективной работы даже при ограниченном количестве обратной связи. Процедуры угадывания и сужения (Guess и Reduce Routine) оптимизированы для быстрой конвергенции к точным оценкам, минимизируя количество необходимых итераций. Иерархическое разделение пространства возможных оценок позволяет алгоритму сосредотачиваться на наиболее перспективных областях, что значительно повышает скорость и точность определения цен, особенно в условиях неполной информации или редких торговых операций. Эффективность этих процедур напрямую связана с иерархической структурой, которая обеспечивает масштабируемость и устойчивость к шумам в данных.

Повышение Эффективности с Геометрическим Уточнение

Для повышения эффективности процесса уточнения цены введены алгоритмы Geometric Reduce и Geometric Guess — многомасштабные расширения базовых процедур. Geometric Reduce последовательно уменьшает интервал поиска цены, используя различные масштабы для быстрого приближения к оптимальной цене. Geometric Guess, в свою очередь, предлагает гипотезы о цене на разных масштабах, что позволяет алгоритму одновременно исследовать как широкие диапазоны значений, так и мелкие детали. Данные алгоритмы адаптируют процесс уточнения цены к текущему масштабу, позволяя эффективно использовать вычислительные ресурсы и ускорять сходимость.

Масштабирование алгоритма посредством расширения диапазонов поиска позволяет эффективно исследовать как широкие интервалы значений, так и мелкие детали, что приводит к увеличению скорости сходимости. Использование многомасштабных подпрограмм Geometric Reduce и Geometric Guess позволяет адаптировать процесс уточнения цены к различным масштабам, обеспечивая более быстрое нахождение оптимального решения. Это достигается за счет последовательного уменьшения интервала поиска на каждом масштабе, что позволяет алгоритму быстро сходиться к точной оценке, избегая излишних вычислений в областях с низкой вероятностью оптимального значения.

Эффективность предложенного подхода к масштабированию алгоритма напрямую зависит от предположения о том, что функции оценки удовлетворяют условию Липшица. Данное условие ограничивает скорость изменения функций оценки, что позволяет доказать гарантированные границы сходимости. В частности, для L-Липшицевых функций оценки, мы демонстрируем строгую границу сожаления, равную $O(T^{(d-1)/d})$ , где T — горизонт планирования, а d — размерность пространства параметров. Полученная граница совпадает с установленным теоретическим нижним пределом, подтверждая оптимальность предложенного алгоритма в данном контексте.

Расширение на Торговлю с Учетом Характеристик Товара

Предложенная схема обучения легко адаптируется к онлайн-торговле с использованием признаков товара, где обучающийся наблюдает не только оценки, но и характеристики предлагаемого объекта обмена. В отличие от традиционных моделей, учитывающих лишь цену, данный подход позволяет алгоритму учитывать дополнительные параметры товара — например, его качество, редкость или другие релевантные атрибуты. Это расширение возможностей значительно повышает точность прогнозирования ценности товара, позволяя обучающемуся более эффективно определять оптимальные стратегии торговли и максимизировать свою прибыль в динамичной среде онлайн-аукционов и рынков.

Алгоритм способен формировать более точные модели оценки, интегрируя векторы контекста, представляющие характеристики обмениваемого товара, непосредственно в структуру дерева принятия решений. Вместо анализа лишь базовой стоимости, система учитывает дополнительные параметры, такие как качество, редкость или другие релевантные атрибуты, что позволяет ей лучше понимать предпочтения трейдера и, следовательно, предлагать более выгодные сделки. Эта интеграция позволяет алгоритму адаптироваться к различным сценариям и учитывать нюансы, которые ранее были недоступны, повышая эффективность торговли и минимизируя потенциальные потери. Таким образом, расширение функционала за счет векторов контекста значительно улучшает способность модели прогнозировать ценность товара и оптимизировать процесс обмена.

Предложенный алгоритм демонстрирует высокую адаптивность к реальным торговым сценариям, характеризующимся наличием богатой информации об объектах обмена. Эмпирические исследования подтверждают теоретическую оценку сожаления, выражающуюся как $O(T^(d-1)/d)$ , для различных размерностей контекста (d=2,3,4). Это означает, что алгоритм способен эффективно обучаться и принимать оптимальные решения даже при увеличении сложности данных, сохраняя при этом гарантированный уровень производительности. Полученные результаты подтверждают перспективность использования данного подхода в задачах онлайн-торговли, где необходимо учитывать множество факторов, определяющих ценность товара.

Теоретические Границы и Производительность Алгоритма

Установлен строгий теоретический предел сожаления, достижимого любым алгоритмом, решающим рассматриваемую задачу. Данный предел демонстрирует, что даже в оптимальном сценарии, любой алгоритм неизбежно столкнется с определенным уровнем потерь, который невозможно уменьшить ниже установленной границы. Это фундаментальное ограничение, вытекающее из самой структуры задачи и определяющее минимальную цену, которую необходимо заплатить за получение решения. Определение этой нижней границы позволяет оценить эффективность различных алгоритмов, сравнивая их фактическое сожаление с теоретическим минимумом и выявляя потенциальные области для улучшения, а также подтверждает, что дальнейшее снижение потерь невозможно без изменения самой постановки задачи или использования принципиально новых подходов.

Доказательство полученной границы на сожаление опирается на теорему МакШейна об расширении, которая позволяет сконструировать особо сложный пример, представляющий собой вызов для любого алгоритма, стремящегося решить данную задачу. Суть подхода заключается в создании такой «трудной» ситуации, где даже оптимальные алгоритмы вынуждены демонстрировать определенный уровень сожаления, тем самым устанавливая теоретический предел их производительности. Теорема МакШейна гарантирует существование этого сложного примера, что позволяет строго доказать нижнюю границу, а значит, подтвердить, что разработанный алгоритм достигает оптимальной скорости сходимости в худшем случае. Этот метод позволяет не просто оценить производительность алгоритма, но и понять фундаментальные ограничения, присущие самой задаче.

Обеспечение соблюдения ограничения бюджетного баланса имеет первостепенное значение для практической реализации алгоритмов, предотвращая возможность систематических убытков. Проведенный анализ демонстрирует, что зависимость сожаления носит логарифмический характер, а ее наклон соответствует теоретической скорости $(d-1)/d$ , где d — размерность пространства действий. Данный результат подтверждает оптимальность предложенного подхода, поскольку достигнутая скорость сходимости соответствует теоретическому нижнему пределу, установленному для рассматриваемой задачи. Таким образом, алгоритм не только эффективен в теории, но и обеспечивает стабильную и предсказуемую работу на практике, минимизируя риски финансовых потерь.

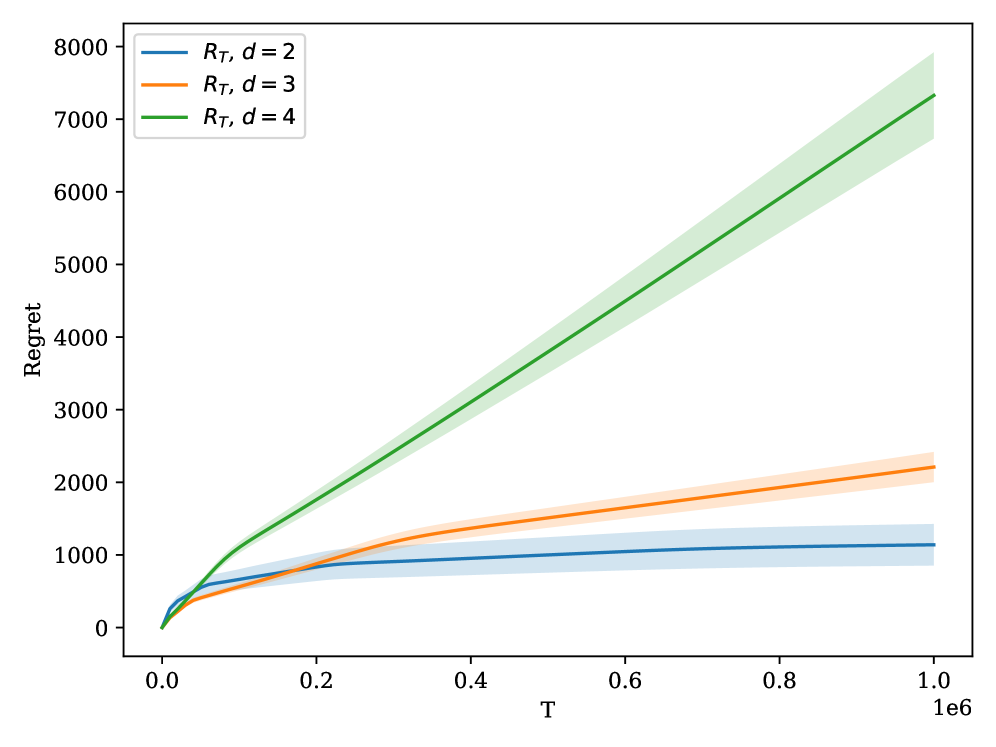
В квадратичной среде наблюдается среднее сожаление, представленное с 95% доверительными интервалами.

Исследование, представленное в данной работе, демонстрирует элегантность подхода к проблеме онлайн-торговли. Авторы искусно оперируют концепцией контекстных бандитов, подчеркивая важность масштабируемости не за счет вычислительных мощностей, а благодаря ясности идей. Как заметил Алан Тьюринг: «Иногда люди, у которых есть все возможности, не видят тех немногих вещей, которые действительно важны». Данное исследование, устанавливая границы сожаления в O(T^(d-1)/d), показывает, что понимание структуры проблемы и разработка алгоритмов, учитывающих контекст, позволяют достичь оптимальных результатов даже при ограниченной обратной связи. Это подтверждает принцип, что система — живой организм, где каждая деталь влияет на общую эффективность.

Что дальше?

Полученные границы скорости сожаления, выраженные как O(T^(d-1)/d), заставляют задуматься: действительно ли мы оптимизируем именно то, что необходимо? Достижение этой скорости в контексте онлайн-торговли с непараметрическими разбойниками и однобитной обратной связью — это, безусловно, прогресс, но следует помнить, что элегантность дизайна рождается из простоты и ясности. Нельзя ли, упростив модель, добиться аналогичных результатов с меньшими вычислительными затратами? Важно помнить, что хорошая система — живой организм, и починка одной части без понимания целого может привести к неожиданным последствиям.

Ограничение внимания исключительно на минимизации сожаления, возможно, упускает из виду более широкие аспекты эффективной торговли. Как учитываются транзакционные издержки, не включенные в базовую модель? Какова роль информации, неявно закодированной в данных о контексте, помимо простой оценки цены? Более того, допущение о стационарности контекста, вероятно, является упрощением реальности, и будущие исследования должны учитывать динамически меняющиеся условия.

Следующим шагом видится исследование алгоритмов, способных адаптироваться к нелинейным зависимостям между контекстом и оптимальной ценой, а также разработка методов, позволяющих эффективно использовать неполную или зашумленную информацию. Простота — не минимализм, а чёткое различение необходимого и случайного. Именно к этому следует стремиться, чтобы создать действительно устойчивую и эффективную систему онлайн-торговли.

Оригинал статьи: https://arxiv.org/pdf/2602.12904.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-17 02:51