Трансформеры решают сложные задачи: от оптимизации до принятия решений

Автор: Денис Аветисян

Новое исследование демонстрирует, как архитектура трансформеров может эффективно применяться для решения задач квадратичного программирования и оптимизации портфеля активов.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Оптимальная конфигурация LinearTransformer, включающая 8 слоёв и 2 головы, при параметрах [latex]n=10[/latex] и [latex]m=3n=10[/latex], демонстрирует чёткое распределение ошибок, указывающее на высокую эффективность данной архитектуры в задачах, требующих точной обработки последовательностей. — Оптимальная конфигурация LinearTransformer, включающая 8 слоёв и 2 головы, при параметрах $n=10$ и $m=3n=10$ , демонстрирует чёткое распределение ошибок, указывающее на высокую эффективность данной архитектуры в задачах, требующих точной обработки последовательностей.

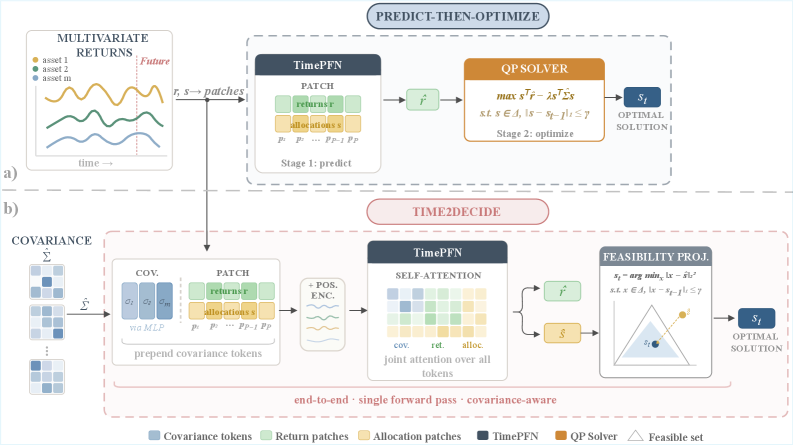
В статье представлен метод, использующий информацию о ковариации для повышения эффективности трансформеров в задачах оптимизации и принятия решений в реальном времени.

Традиционные подходы к задачам квадратичного программирования и оптимизации часто требуют итеративных вычислений, ограничивая их применение в задачах принятия решений в реальном времени. В работе ‘Covariance-Aware Transformers for Quadratic Programming and Decision Making’ предложен новый подход, использующий архитектуру трансформеров для решения задач квадратичного программирования, особенно эффективный при работе с ковариационными матрицами. Показано, что трансформеры, обогащенные информацией о ковариации, демонстрируют превосходные результаты в задачах оптимизации, таких как построение портфеля, превосходя как итеративные методы, так и стандартные процедуры «предсказать-оптимизировать». Не откроет ли это путь к созданию end-to-end систем принятия решений, способных эффективно использовать информацию второго порядка для решения сложных оптимизационных задач?

За пределами Прогнозов: Вызовы Последовательного Принятия Решений

Многие задачи, с которыми сталкивается современный мир — от управления финансовыми потоками до разработки стратегий в играх и роботизированной навигации — требуют последовательного принятия оптимальных решений в условиях неопределенности. В отличие от статических проблем, где решение находится единожды, эти задачи подразумевают серию действий, каждое из которых влияет на последующие. Неизбежная неполнота информации о будущем состоянии системы, а также случайные факторы, усложняют процесс выбора наилучшего варианта на каждом этапе. Эффективное решение подобных задач требует не просто прогнозирования, но и способности адаптироваться к изменяющимся обстоятельствам и учитывать вероятностные исходы, что делает их особенно сложными и интересными для исследователей в области искусственного интеллекта и теории принятия решений.

Традиционные подходы к принятию последовательных решений часто опираются на прогнозирование будущих состояний системы, что неизбежно приводит к накоплению ошибок. Каждое предсказание, даже незначительно отклоняющееся от реальности, вносит погрешность в последующие этапы планирования, усугубляя ее с течением времени. Это особенно заметно в динамичных средах, где неопределенность высока и долгосрочное прогнозирование становится практически невозможным. В результате, стратегии, основанные на предсказаниях, теряют свою эффективность, а система демонстрирует ограниченную способность адаптироваться к изменяющимся условиям. Вместо этого, современные исследования направлены на разработку методов, позволяющих принимать решения, опираясь на текущую информацию и минимизируя зависимость от неточных прогнозов будущего.

В отличие от подхода «Предсказать-Затем-Оптимизировать», который разделяет прогнозирование доходностей $\hat{r}_{t}$ и оптимизацию распределения активов $s_{t}$ , Time2Decide объединяет эти этапы в единый проход, используя совместное внимание для обработки токенов ковариации $\hat{\Sigma}_{t}$ , доходностей и распределения, что позволяет напрямую получить оптимальное распределение $s_{t}$ с учетом ковариации без отдельного этапа оптимизации.

Квадратичное Программирование: Основа Оптимизации

Квадратичное программирование (КП) представляет собой мощный математический аппарат для задач оптимизации, в которых целевая функция является квадратичной, а ограничения линейными. Формально, задача КП может быть записана как минимизация $\frac{1}{2}x^T Q x + c^T x$ при ограничениях $A x \leq b$ , где $x$ — вектор переменных, $Q$ — симметричная матрица, $c$ — вектор, $A$ — матрица ограничений, а $b$ — вектор ограничений. Эффективность КП обусловлена наличием хорошо разработанных алгоритмов решения, таких как метод активных множеств и методы внутренней точки, позволяющих находить оптимальные решения для широкого класса задач, возникающих в различных областях, включая финансы, машинное обучение и инженерию.

Неограниченные квадратичные задачи оптимизации (QP) могут быть эффективно решены итеративными методами, такими как метод градиентного спуска (GradientDescent). В частности, для задач вида $\min_x \frac{1}{2}x^T Q x + c^T x$ , где Q — симметричная положительно определенная матрица, градиентный спуск гарантированно сходится к оптимальному решению. Однако, добавление ограничений (например, линейных равенств или неравенств) значительно усложняет процесс решения. Для решения QP с ограничениями требуются более сложные алгоритмы, такие как методы активного множества, методы внутренней точки или методы последовательного квадратичного программирования, которые учитывают ограничения на каждой итерации и требуют решения систем линейных уравнений с матрицами, зависящими от ограничений.

Методы L1-регуляризации и L1-ограничения, реализуемые посредством проксимальных операторов, позволяют повысить разреженность решения в задачах квадратичного программирования. L1-регуляризация добавляет к целевой функции штраф, пропорциональный абсолютной сумме коэффициентов, что стимулирует обнуление незначимых параметров. L1-ограничение напрямую ограничивает сумму абсолютных значений коэффициентов. Применение проксимальных операторов эффективно решает возникающие подзадачи, комбинируя оптимизацию целевой функции с соблюдением ограничений. Такой подход особенно полезен в задачах, где важна интерпретируемость модели или требуется выборка наиболее значимых признаков, поскольку разреженные решения содержат меньше ненулевых элементов, упрощая анализ и снижая вычислительную сложность.

Трансформерная модель демонстрирует сходимость, сопоставимую с базовыми алгоритмами градиентного спуска (GD), ускоренного градиентного спуска ISTA и проективного градиентного спуска (PGD) в неконстрейнных, регуляризованных и констрейнных задачах соответственно, что подтверждается близким совпадением кривых сходимости на семитрилогарифмическом графике.

Предсказать, Затем Оптимизировать: Двухэтапный Подход

Метод «Предсказать-затем-оптимизировать» (Predict-then-Optimize) представляет собой декомпозицию задачи на два последовательных этапа. На первом этапе формируется прогноз будущих состояний системы, используя исторические данные и модели прогнозирования. Полученные прогнозы служат входными данными для второго этапа, на котором решается задача квадратичного программирования (QP). Задача QP формулируется таким образом, чтобы оптимизировать целевую функцию при заданных ограничениях, используя спрогнозированные состояния. В результате, решение QP определяет оптимальные действия или параметры управления, которые должны быть применены в будущем, основываясь на предсказанном сценарии. $min \frac{1}{2}x^T Q x + c^T x$ , где Q — матрица квадратичных коэффициентов, а c — вектор линейных коэффициентов.

В основе предложенного подхода лежит использование TimePFN — мощной нейронной сети, предназначенной для генерации прогнозов временных рядов. TimePFN (Temporal Point Flow Network) использует механизм потоков точек для моделирования динамики временных данных, что позволяет эффективно захватывать сложные зависимости и долгосрочные тренды. Архитектура сети обеспечивает высокую точность прогнозирования, особенно в задачах, требующих предсказания значений на горизонте, превышающем возможности традиционных рекуррентных сетей. Её способность к экстраполяции и моделированию нелинейных зависимостей делает TimePFN ключевым компонентом в процессе прогнозирования, необходимом для последующей оптимизации в рамках предложенной схемы «Predict-then-Optimize».

Последовательная природа подхода «Предсказать-оптимизировать» вносит задержки в процесс принятия решений, поскольку оптимизация не может начаться до получения прогноза. Производительность системы напрямую зависит от точности первоначальных прогнозов; ошибки в прогнозировании приводят к субоптимальным результатам, особенно в сценариях, где калибровка имеет решающее значение, например, при управлении энергопотреблением или поддержании стабильности сети. В таких случаях, даже незначительные неточности в прогнозах могут привести к значительным отклонениям от желаемого результата и потребовать дополнительных корректировок, увеличивая общую задержку и снижая эффективность системы.

Экспериментальные данные подтверждают, что метод обучения сквозь обучение (end-to-end) демонстрирует более низкое сожаление и стабильную точность в условиях растущей силы сигнала, в отличие от подхода предсказать-а-оптимизировать (PtO), который уступает в эффективности из-за фиксированного коэффициента сжатия [latex] \ho=1 [/latex]. — Экспериментальные данные подтверждают, что метод обучения сквозь обучение (end-to-end) демонстрирует более низкое сожаление и стабильную точность в условиях растущей силы сигнала, в отличие от подхода предсказать-а-оптимизировать (PtO), который уступает в эффективности из-за фиксированного коэффициента сжатия $\ho=1$ .

Time2Decide: Прямая Оптимизация с Учетом Ковариации

Метод Time2Decide представляет собой инновационный подход к принятию решений, объединяющий процесс оптимизации в единый этап. В его основе лежит архитектура TimePFN, позволяющая эффективно обрабатывать временные последовательности, и метод квадратичного программирования, обеспечивающий нахождение оптимальных решений. В отличие от традиционных подходов, требующих последовательного предсказания и последующей оптимизации, Time2Decide непосредственно преобразует входные данные в оптимальные действия, что значительно повышает скорость и эффективность принятия решений в динамичных средах. Такой подход позволяет не только снизить вычислительные затраты, но и добиться более стабильных и точных результатов, особенно в условиях неопределенности и шума.

Метод Time2Decide эффективно интегрирует неопределенность в процесс оптимизации благодаря применению технологии CovarianceAugmentation. Данный подход позволяет модели учитывать ковариацию между различными переменными, что критически важно при принятии решений в условиях неполной информации или зашумленных данных. Вместо того, чтобы полагаться на точечные прогнозы, Time2Decide расширяет пространство поиска решений, учитывая вероятностное распределение возможных исходов. Это достигается путем аугментации входных данных ковариационной матрицей, которая описывает взаимосвязь между различными источниками неопределенности. Такой подход позволяет не только повысить робастность системы к шумам и ошибкам, но и улучшить качество принимаемых решений, поскольку модель способна более адекватно оценивать риски и выбирать оптимальные стратегии в динамически меняющихся условиях. В результате, Time2Decide демонстрирует превосходство над традиционными методами, основанными на предсказании и последующей оптимизации, особенно в задачах, где точность прогнозов ограничена.

Метод Time2Decide демонстрирует значительное повышение эффективности за счет использования механизма LinearAttention. Данная технология позволяет осуществлять управление в реальном времени даже в сложных средах, при этом наблюдаемый прирост вычислительной нагрузки составляет всего 1.04 — 1.35 по сравнению с классическими алгоритмами, такими как Gradient Descent и ISTA. Такая оптимизация вычислений делает Time2Decide особенно привлекательным для приложений, требующих быстрого принятия решений и ограниченных вычислительных ресурсов, открывая возможности для использования в робототехнике, автономных системах и других динамичных областях.

Предложенный подход, Time2Decide, стремится к приближению к $BayesOptimalPolicy$ , что обеспечивает повышенную производительность и устойчивость системы принятия решений. Эксперименты по обучению ковариациям демонстрируют впечатляющий результат — коэффициент детерминации $R^2$ достиг значения 0.9935. Данный показатель значительно превосходит результат, полученный с использованием BasicLinearTransformer, у которого $R^2$ составил лишь 0.2827. Это указывает на способность Time2Decide более точно моделировать неопределенность и, следовательно, принимать более обоснованные и надежные решения в сложных условиях.

Экспериментальные данные демонстрируют устойчивое превосходство Time2Decide над подходами, основанными на предсказании с последующей оптимизацией. В частности, Time2Decide характеризуется значительно меньшим сожалением о принятых решениях и более стабильной ошибкой в условиях зашумленных данных. Это указывает на повышенную робастность алгоритма и его способность эффективно функционировать в реальных сценариях, где данные часто содержат погрешности и неопределенности. Полученные результаты подтверждают, что прямой подход к оптимизации, реализованный в Time2Decide, позволяет добиться большей точности и надежности в принятии решений по сравнению с методами, требующими предварительного прогнозирования.

Исследование демонстрирует, что трансформеры, усиленные информацией о ковариации, способны эффективно решать задачи квадратичного программирования и, как следствие, достигать передовых результатов в задачах принятия решений, таких как оптимизация портфеля. Этот подход, по сути, рассматривает реальность как открытый исходный код, который еще предстоит расшифровать. Как заметила Барбара Лисков: «Хороший дизайн — это когда система достаточно ясна, чтобы ты мог изменить ее, не сломав ничего». Подобно тому, как тщательно спроектированная система позволяет вносить изменения без непредсказуемых последствий, так и грамотное использование ковариации в трансформерах позволяет добиться стабильной и надежной оптимизации, даже в сложных задачах принятия решений.

Куда же дальше?

Представленная работа, демонстрируя способность трансформеров к решению задач квадратичного программирования, открывает двери, но не гарантирует легкой прогулки. Успех, подкрепленный учетом ковариации, наводит на мысль: возможно, дело не в самой архитектуре, а в умении правильно оперировать информацией о неопределенности. Следующим шагом видится не просто увеличение размера модели или усложнение алгоритмов, а глубокое понимание того, как эта ковариационная информация влияет на процесс оптимизации. Что, если существуют более элегантные способы ее кодирования, не требующие прямого ввода?

Очевидным ограничением является применимость к задачам, где ковариационные структуры относительно стабильны. Реальный мир редко предлагает такую роскошь. Будущие исследования должны быть направлены на разработку методов адаптации к изменяющимся ковариациям, возможно, с использованием рекуррентных механизмов или мета-обучения. Необходимо также изучить, как эти методы сочетаются с другими подходами к оптимизации, такими как стохастический градиентный спуск, чтобы создать гибридные системы, использующие сильные стороны каждой парадигмы.

В конечном итоге, задача не в создании «идеального» алгоритма, а в создании инструментов, позволяющих нам взламывать ограничения реальности. Трансформеры, возможно, лишь один из таких инструментов, но их способность к обучению и адаптации делает их достойными пристального внимания. Истина, как всегда, лежит где-то между теорией и практикой, между математической строгостью и эмпирическим подтверждением.

Оригинал статьи: https://arxiv.org/pdf/2602.14506.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-18 01:00