Укрощение сложности: Данные на службе у динамических систем

Автор: Денис Аветисян

Новый подход позволяет эффективно моделировать сложные динамические системы, используя данные и методы стохастического понижения размерности.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Предложенный стохастический подход к сокращенному порядку моделирования (ROM) включает в себя вероятностный энкодер, латентное стохастическое дифференциальное уравнение (SDE) и вероятностный декодер, позволяя, на основе параметров μ, вынуждающей функции [latex]f(t)[/latex] и начального условия [latex]u_0[/latex], кодировать начальное условие в латентное пространство, решать латентное SDE для получения траекторий и декодировать полученные траектории для прогнозирования стохастического отклика исходной полномасштабной модели (FOM) [latex]u(t)[/latex], что позволяет получить как среднее значение прогноза, так и статистические границы погрешности. — Предложенный стохастический подход к сокращенному порядку моделирования (ROM) включает в себя вероятностный энкодер, латентное стохастическое дифференциальное уравнение (SDE) и вероятностный декодер, позволяя, на основе параметров μ, вынуждающей функции $f(t)$ и начального условия $u_0$ , кодировать начальное условие в латентное пространство, решать латентное SDE для получения траекторий и декодировать полученные траектории для прогнозирования стохастического отклика исходной полномасштабной модели (FOM) $u(t)$ , что позволяет получить как среднее значение прогноза, так и статистические границы погрешности.

В статье представлен метод построения стохастических моделей пониженной размерности на основе данных с применением вариационного вывода и амортизирующей инференции.

Вычислительное моделирование сложных динамических систем, зависящих от параметров, часто сталкивается с ограничениями, обусловленными высокой вычислительной стоимостью. В данной работе, посвященной ‘Data-driven stochastic reduced-order modeling of parametrized dynamical systems’, предложен новый подход к построению стохастических моделей пониженной размерности, основанный на данных и вариационном выводе. Разработанный метод позволяет эффективно прогнозировать поведение систем при различных параметрах и внешних воздействиях, избегая необходимости в явном решении исходных уравнений. Открывает ли это путь к созданию более надежных и эффективных инструментов для анализа и управления сложными процессами в различных областях науки и техники?

Вызов высокой размерности: где теория встречает практику

Многие задачи в науке и технике требуют построения моделей сложных систем, описываемых уравнениями с огромным числом переменных — так называемыми полномасштабными (Full-Order) моделями. Эти модели, возникающие, например, при моделировании турбулентных потоков, сложных химических реакций или поведения больших энергетических сетей, характеризуются высокой размерностью, что делает их непосредственное численное решение крайне трудоемким и зачастую невозможным. Размерность этих моделей может достигать тысяч и даже миллионов переменных, что предъявляет огромные требования к вычислительным ресурсам и времени, необходимым для получения результатов. В связи с этим, разработка эффективных методов снижения размерности моделей является актуальной и востребованной задачей, позволяющей значительно ускорить процесс моделирования и анализа сложных систем.

Прямое моделирование сложных систем, описываемых полномасштабными моделями с высокой размерностью, зачастую сталкивается с непреодолимыми вычислительными трудностями. Необходимость в обработке огромных объемов данных и продолжительные расчеты делают подобные симуляции непрактичными, особенно при анализе динамически изменяющихся процессов. В связи с этим, возникает потребность в применении методов снижения размерности, позволяющих упростить модель без существенной потери точности. Эти методы, фокусируясь на выделении ключевых параметров и закономерностей, значительно сокращают вычислительные затраты и открывают возможности для эффективного анализа и прогнозирования поведения сложных систем в различных областях науки и техники. $y = f(x)$ — пример упрощенного представления сложной зависимости, которое часто используется в моделях пониженной размерности.

Традиционные методы понижения размерности, применяемые для упрощения сложных систем, зачастую испытывают трудности при работе со случайными (стохастическими) процессами. Это связано с тем, что стандартные алгоритмы, как правило, предполагают детерминированность модели и не учитывают влияние случайных возмущений или неопределенностей. Для преодоления этих ограничений, а также для получения точных результатов, классические подходы часто требуют значительных вычислительных ресурсов и большого объема данных, полученных в результате многочисленных расчетов или экспериментальных измерений. По сути, для адекватного представления стохастической системы с использованием пониженной модели, необходимо «обучить» алгоритм на обширном наборе данных, что может быть чрезвычайно затратно по времени и ресурсам, особенно в случаях, когда сбор данных затруднен или невозможен.

Снимки решения уравнения реакционно-диффузионной системы демонстрируют её эволюцию во времени и пространстве.

Вариационный вывод для сокращенных моделей: новый взгляд на сложность

В основе предложенного фреймворка для построения сокращенных порядковых моделей (ROM_Framework) лежит метод вариационного вывода, используемый для обучения низкоразмерному латентному пространству (Latent_Space), представляющему динамику системы. Вместо прямого решения исходной системы уравнений, вариационный вывод позволяет аппроксимировать распределение вероятностей состояний системы в этом латентном пространстве. Это достигается путем обучения энкодера, отображающего высокоразмерные данные траектории (Trajectory_Data) в латентное пространство, и декодера, восстанавливающего траекторию из латентного представления. Таким образом, динамика системы моделируется в более компактном и управляемом пространстве, что существенно снижает вычислительные затраты и упрощает анализ.

Схема амортизированного стохастического вариационного вывода (Amortized_SVI) обеспечивает эффективное обучение модели, избегая необходимости в многократных прямых расчетах (forward solves). В традиционных подходах вариационного вывода, параметры априорного распределения оптимизируются индивидуально для каждого набора данных. Amortized_SVI использует нейронную сеть — энкодер — для отображения входных данных в параметры распределения, что позволяет выполнять вывод для новых данных значительно быстрее. Этот подход позволяет эффективно аппроксимировать апостериорное распределение, уменьшая вычислительные затраты и делая обучение более масштабируемым для больших наборов данных и сложных динамических систем. Фактически, Amortized_SVI позволяет избежать итеративного решения прямой задачи для каждого шага обучения, что существенно ускоряет процесс.

В рамках разработанного подхода используется вариационный автоэнкодер (VAE) для установления соответствия между высокоразмерными данными траекторий (Trajectory_Data) и латентным пространством. VAE представляет собой нейронную сеть, состоящую из энкодера и декодера. Энкодер преобразует входные данные траекторий в вероятностное распределение в латентном пространстве, характеризуемое средним значением и дисперсией. Декодер, напротив, реконструирует исходные данные траекторий из точек, выбранных из этого распределения. Обучение VAE осуществляется путем минимизации функции потерь, включающей как ошибку реконструкции, так и дивергенцию Кулбака-Лейблера, что обеспечивает компактное и информативное представление динамики системы в латентном пространстве.

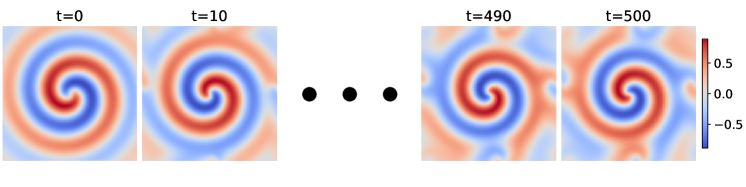
Динамика в латентном пространстве описывается стохастическим дифференциальным уравнением (SDE). Это позволяет моделировать стохастические процессы, возникающие в исходной динамической системе, в значительно более низкоразмерном пространстве. $dS_t = f(S_t)dt + g(S_t)dW_t$ , где $S_t$ — состояние в латентном пространстве в момент времени t, f — функция дрейфа, g — функция диффузии, а $dW_t$ — винеровский процесс. Использование Latent_SDE обеспечивает возможность захвата неопределенностей и случайных возмущений, что критически важно для точного моделирования сложных динамических систем, особенно в задачах, связанных с прогнозированием и управлением.

Проверка и сравнение: где теория встречается с реальностью

Для оценки эффективности разработанного фреймворка ROM_Framework была проведена сравнительная оценка с использованием общепринятых базовых методов, а именно параметризованных нейронных обыкновенных дифференциальных уравнений (PNODE) и параметризованных нейронных стохастических дифференциальных уравнений (PNSDE). Данные методы были выбраны в качестве эталонных для обеспечения объективной оценки производительности и выявления преимуществ предложенного подхода в решении задач снижения размерности. Сравнение проводилось на идентичных наборах данных и с использованием унифицированных метрик оценки для обеспечения сопоставимости результатов.

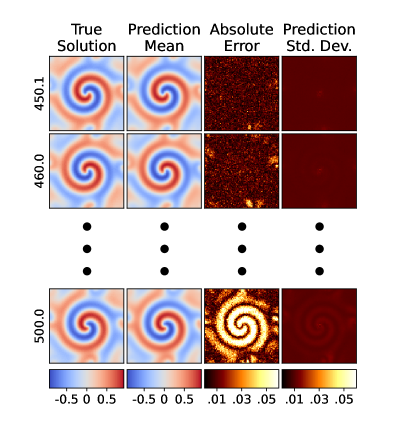
Результаты оценки предложенного ROM_Framework на задаче моделирования потока жидкости в 105,600-мерном пространстве показали среднюю ошибку в 0.036. Данный показатель превосходит результаты, полученные с использованием Parametrized Neural Ordinary Differential Equations (PNODE), где средняя ошибка составила 0.076, и Parametrized Neural Stochastic Differential Equations (PNSDE) с ошибкой 0.091. Полученные данные свидетельствуют о более высокой точности предложенного подхода в решении задач моделирования сложных потоков жидкости по сравнению с рассмотренными базовыми методами.

Использование вариационного вывода, формализованного через нижнюю оценку правдоподобия (Evidence Lower Bound — ELBO), обеспечивает надежную оценку неопределенности в предсказаниях модели. ELBO представляет собой границу снизу для логарифма маргинальной вероятности данных, что позволяет аппроксимировать распределение апостериорной вероятности, необходимое для количественной оценки неопределенности. В рамках разработанного подхода, максимизация ELBO приводит к обучению модели, способной не только предсказывать значения, но и предоставлять информацию о доверии к этим предсказаниям, что критически важно для приложений, требующих надежной оценки рисков и принятия обоснованных решений.

При тестировании предложенного подхода на различных функциях принуждения (Forcing_Function) и в различных сценариях, было достигнуто превосходство по времени обучения, составившее 3.281 часа. Для сравнения, время обучения моделей PNODE и PNSDE составило 6.035 и 4.407 часа соответственно. Данные результаты демонстрируют значительное повышение эффективности предложенного метода в контексте обучения на сложных задачах моделирования.

Анализ реакции-диффузии показывает, что предсказанные значения точно соответствуют истинному решению как для чистых, так и для зашумленных данных, что подтверждается низким значением абсолютной ошибки и малым разбросом предсказаний (см. видео S1-S2).

К интерпретируемой динамике и дальнейшим перспективам: взгляд в будущее

Предлагаемый подход позволяет создать сжатое представление динамических систем в латентном пространстве, что значительно упрощает применение методов открытия моделей, таких как Sparse Identification of Nonlinear Dynamics (SINDy). Благодаря уменьшению размерности исходных данных, SINDy получает возможность эффективно выявлять ключевые нелинейные связи и формулировать интерпретируемые уравнения, описывающие поведение системы. Такой подход позволяет не только моделировать динамику, но и получать ценные сведения о фундаментальных физических принципах, лежащих в её основе, что открывает возможности для более глубокого понимания и прогнозирования поведения сложных систем. Это особенно важно в случаях, когда исходные данные характеризуются высокой размерностью и сложностью, затрудняющими традиционные методы анализа.

Получение интерпретируемых управляющих уравнений из редуцированной модели представляет собой ключевой аспект данной работы. Благодаря компактному представлению динамики в латентном пространстве, становится возможным применение методов обнаружения моделей, таких как SINDy (Sparse Identification of Nonlinear Dynamics). Этот подход позволяет выделить аналитические выражения, описывающие взаимосвязи между переменными состояния, что дает возможность понять фундаментальные физические принципы, лежащие в основе изучаемой системы. Выделенные уравнения не просто описывают наблюдаемое поведение, но и предоставляют ценную информацию о механизмах, определяющих динамику, что существенно расширяет возможности анализа и прогнозирования.

Возможность обучения и представления сложных динамических систем с использованием Deep_Kernel открывает широкие перспективы для применения в различных областях науки и техники. Данный подход позволяет эффективно моделировать и анализировать процессы, характеризующиеся высокой степенью нелинейности и многомерности, что особенно актуально для таких дисциплин, как гидродинамика, метеорология и биофизика. Использование Deep_Kernel позволяет извлекать ключевые признаки и зависимости, скрытые в больших объемах данных, и строить компактные модели, сохраняющие высокую точность прогнозирования. Перспективными направлениями исследований являются адаптация метода к системам с неполной информацией, разработка алгоритмов обучения с подкреплением для управления сложными процессами и интеграция с физически обоснованными моделями для повышения интерпретируемости и надежности результатов.

Разработанный подход демонстрирует значительное снижение размерности исходного пространства состояний — с 105 600 до всего лишь 7 измерений — при этом сохраняя высокую точность прогнозирования. Это позволяет не только упростить анализ и моделирование сложных систем, но и существенно снизить вычислительные затраты. В перспективе, планируется расширение возможностей данной методики для работы с еще более сложными динамическими системами, а также интеграция методов обучения с учетом физических принципов, что позволит получать не только компактные, но и физически обоснованные модели, способные к более глубокому пониманию и управлению сложными процессами.

Изучение методов стохастического понижения размерности, представленное в статье, неизбежно напоминает о вечной борьбе между теорией и практикой. Авторы предлагают элегантный способ построения моделей, но всегда следует помнить: продакшен найдет способ сломать даже самый изящный алгоритм. Как говорил Пол Эрдёш: «Математика — это искусство находить закономерности в хаосе, а программирование — искусство создавать хаос в закономерностях». Истина в том, что любая «революционная» технология, предложенная в этой работе, завтра же станет техническим долгом, требующим постоянного обслуживания и адаптации к реальным условиям. Особенно учитывая сложность моделирования динамических систем, где даже небольшие отклонения в начальных данных могут привести к катастрофическим последствиям. Так что, да, стохастическое понижение размерности — это интересно, но главное — подготовиться к неизбежному хаосу.

Что дальше?

Представленные методы, безусловно, позволяют строить некие “управляемые” модели динамических систем, избегая необходимости в явном знании полномасштабной модели. Однако, как показывает опыт миграций, каждое упрощение — это будущий техдолг. Идея “самовосстанавливающихся” моделей, основанных на вариационном выводе, пока что просто не встретила достаточно сложных входных данных. Стоит помнить, что если ошибка воспроизводится, значит, у нас стабильная система — а стабильность, как известно, враг прогресса.

В ближайшем будущем, вероятно, усилия будут направлены на повышение робастности этих моделей к шумам и неполноте данных. Вместо погони за идеальным сжатием, стоит обратить внимание на разработку методов оценки достоверности предсказаний. Документация, конечно, останется формой коллективного самообмана, но хотя бы попытаться её вести нужно.

И, конечно, не стоит забывать о фундаментальных ограничениях. Любая попытка заменить физику статистикой — это лишь временное решение. Когда-нибудь найдется случай, когда даже самые изящные нейронные сети окажутся бессильны перед законами природы. И тогда придётся возвращаться к ручным расчётам и переписывать всё с нуля.

Оригинал статьи: https://arxiv.org/pdf/2601.10690.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-17 07:46