Укрощение Волатильности: Оптимальная Адаптация в Изменяющихся Условиях

Автор: Денис Аветисян

В новой работе представлена общая теория оптимального принятия решений в стохастических средах с меняющимися ограничениями, позволяющая минимизировать издержки адаптации.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

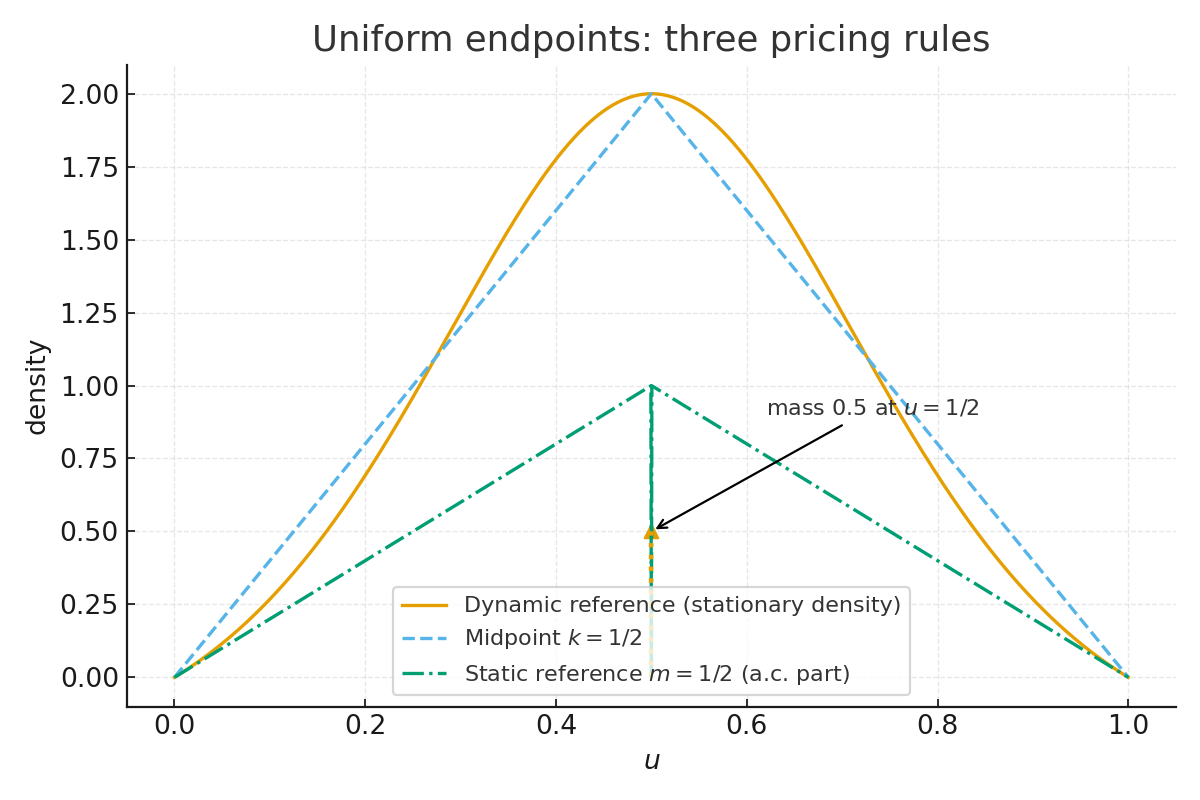
Бесплатный Телеграм канал

В условиях квадратичной изменчивости оптимальная политика, полученная посредством уравнения Беллмана для средней стоимости, аппроксимируется функцией [latex]r^{\ast}(s)[/latex], плавно переходящей между правилом Status Quo (45°) и правилом якорения, и смещающей действие к значению 0.5s с наклоном около 0.88, однако прирост эффективности оказывается незначительным, поскольку правило Status Quo обеспечивает более 99% от теоретического предела. — В условиях квадратичной изменчивости оптимальная политика, полученная посредством уравнения Беллмана для средней стоимости, аппроксимируется функцией $r^{\ast}(s)$ , плавно переходящей между правилом Status Quo (45°) и правилом якорения, и смещающей действие к значению 0.5s с наклоном около 0.88, однако прирост эффективности оказывается незначительным, поскольку правило Status Quo обеспечивает более 99% от теоретического предела.

Исследование демонстрирует, что стратегии, минимизирующие волатильность, часто опираются на ‘опорные правила’ и определяет условия, при которых конкретные цели приводят к различным оптимальным стратегиям.

В условиях неопределенности и изменчивости экономических сред, минимизация волатильности и затрат на адаптацию часто сталкивается с ограничениями, обусловленными динамически меняющимся пространством допустимых действий. В работе ‘Minimizing Volatility: Optimal Adjustment with Evolving Feasibility Constraints’ разработана общая теория оптимального принятия решений в стохастических средах, демонстрирующая, что стратегии, минимизирующие затраты на корректировку, часто основаны на “опорных правилах” — действиях, привязанных к прошлым решениям или фиксированным целям. Показано, что оптимальные механизмы зависят от специфики целевой функции, например, минимизации дисперсии, и могут существенно превосходить эвристические подходы, снижая колебания на 50% и более. Каковы перспективы применения полученных результатов для моделирования финансовых рынков, управления цепями поставок и принятия политических решений?

Ограничения Действий: Определение Допустимого Интервала

Любое принятие решений происходит не в вакууме, а в пределах так называемого “Допустимого Интервала” — диапазона возможных действий, ограниченного как внешними, так и внутренними факторами. Внешние ограничения могут включать в себя ресурсные ограничения, законодательные рамки или даже физические законы, в то время как внутренние факторы — это когнитивные способности, мотивация, убеждения и ценности принимающего решение лица. Этот интервал определяет, какие варианты вообще рассматриваются как реалистичные и осуществимые, отсекая непрактичные или невозможные альтернативы. Таким образом, понимание границ Допустимого Интервала критически важно для анализа процесса принятия решений, поскольку именно в его пределах формируется пространство выбора и реализуется волеизъявление.

Интервал возможных действий, в котором происходит принятие решений, не является фиксированным и неизменным. Он постоянно претерпевает изменения под влиянием как внешних воздействий — так называемых “экзогенных шоков”, таких как внезапные экономические кризисы или технологические прорывы, — так и внутренних ограничений, именуемых “эндогенными ограничениями”. Эти внутренние факторы могут включать в себя ресурсы, навыки, убеждения и даже психологические установки, которые формируют рамки допустимого. Постоянное взаимодействие экзогенных шоков и эндогенных ограничений приводит к непрерывному пересмотру границ этого интервала, открывая новые возможности и одновременно закрывая прежние, что оказывает существенное влияние на процесс принятия решений и формирует траекторию развития.

Понятие “окна Овертона” описывает границы допустимого в рамках общественного дискурса, определяя спектр действий, которые считаются приемлемыми для обсуждения и реализации. Это окно не является фиксированным; оно динамически смещается под влиянием различных факторов, включая политические события, социальные движения и изменения в культурных нормах. Изначально радикальные или неприемлемые идеи могут постепенно перемещаться внутрь этого окна, становясь общепринятыми, в то время как ранее допустимые действия могут оказаться за его пределами. Таким образом, “окно Овертона” служит своего рода фильтром, определяющим границы политически и социально возможного, и оказывает значительное влияние на процесс принятия решений и формирования общественного мнения.

Правила Принятия Решений: Навигация в Интервале

Действующие лица при выборе действий в пределах Допустимого Интервала используют различные ‘Правила Принятия Решений’, каждое из которых характеризуется присущими ему систематическими искажениями. Эти правила представляют собой упрощенные эвристики, позволяющие снизить когнитивную нагрузку при оценке альтернатив. Например, правило ‘Сохранения Статус-Кво’ отдает приоритет поддержанию текущего состояния, в то время как правило ‘Середины’ стремится к компромиссу, а правило ‘Якорения’ фокусируется на конкретных целевых значениях. Важно отметить, что выбор конкретного правила и его влияние на итоговое решение зависят от контекста, индивидуальных предпочтений и доступной информации.

Агенты, принимающие решения в рамках допустимого интервала, используют различные правила выбора действий. Правило «Статус-кво» отдает приоритет сохранению текущего состояния, минимизируя изменения. Правило «Середина» стремится к компромиссу, выбирая значение, находящееся в центре допустимого интервала. В свою очередь, правило «Якоря» фокусируется на конкретной целевой величине, используя ее в качестве отправной точки для принятия решения, даже если она не является оптимальной или рациональной.

Принятие решений в рамках допустимого интервала сопряжено с издержками корректировки (Adjustment Costs), которые представляют собой штрафные санкции за отклонение от предыдущих действий или предпочтительных целей. Эти издержки могут быть как прямыми (например, финансовые затраты на переналадку оборудования), так и косвенными (например, временные затраты на адаптацию или психологический дискомфорт). Величина издержек корректировки может варьироваться в зависимости от конкретной ситуации и индивидуальных предпочтений действующего лица, существенно влияя на выбор между альтернативными вариантами действий даже при одинаковой ожидаемой выгоде. Игнорирование издержек корректировки может привести к неоптимальным решениям и снижению эффективности действий.

Стационарные распределения вероятностей демонстрируют, что механическое колебание (пунктир) зависит от интервала, привязка (штрих-пунктир) концентрирует 50% вероятности в целевой точке, минимизируя дисперсию, а инерция (сплошная линия) характеризуется плавным рассеянием, отражающим тенденцию к дрейфу в допустимом интервале вместо коррекции к среднему.

Волатильность и Стабильность в Действиях

Повторное применение правил принятия решений формирует определенную последовательность действий, количественно оцениваемую с помощью показателя ‘Квадратичная Вариация’ — меры степени изменения состояния системы. $Квадратичная Вариация$ рассчитывается как предел суммы квадратов изменений на малых интервалах времени, позволяя оценить общую изменчивость, вызванную последовательным применением конкретного правила. В контексте анализа правил принятия решений, данный показатель позволяет сравнить стабильность или волатильность системы, обусловленную каждым правилом в отдельности, и определить, насколько сильно каждое правило способствует изменению состояния системы с течением времени. Чем ниже значение квадратичной вариации, тем более стабильным является процесс принятия решений.

Применение различных правил принятия решений — “Статус-кво”, “Середина” и “Якорение” — приводит к различной степени изменения системы, что количественно оценивается показателем квадратичной вариации. Каждое правило вносит уникальный вклад в эту вариацию, определяя общую стабильность или волатильность системы. Различия в квадратичной вариации, возникающие при использовании разных правил, позволяют оценить их влияние на динамику системы и прогнозировать ее поведение. Например, правило “Статус-кво” демонстрирует минимальную волатильность, в то время как другие правила могут приводить к более выраженным колебаниям. Анализ этих различий является ключевым для понимания и управления динамикой системы.

В представленном исследовании показано, что правило «Статус-кво» минимизирует волатильность системы. Количественно это выражается в показателе квадратичной вариации, который для данного правила составляет приблизительно $π/12 - 2/9 \approx 0.0396$ . Это значение ниже, чем у правила «Середина», что указывает на более стабильное поведение системы при использовании правила «Статус-кво» в качестве основы для принятия решений. Таким образом, правило «Статус-кво» обеспечивает меньшие изменения в состоянии системы по сравнению с правилом «Середина», что делает его предпочтительным для сценариев, требующих минимизации колебаний.

Дисперсия правила «Статус-кво» составляет приблизительно $π-34$ ≈ 0.0354, что ниже, чем дисперсия правила «Середина», равная 1/24 ≈ 0.0417. Данный показатель количественно характеризует разброс результатов, получаемых при повторном применении соответствующего правила принятия решений. Более низкая дисперсия правила «Статус-кво» указывает на его большую стабильность и предсказуемость по сравнению с правилом «Середина», поскольку разброс значений вокруг среднего значения при использовании «Статус-кво» меньше.

Моделирование двусторонних торгов в течение 50 периодов показывает, что стандартный двойной аукцион (линейное равновесие) обеспечивает теоретически оптимальную эффективность, но характеризуется высокой волатильностью цен, в то время как правило фиксированной цены (пулинговое равновесие) обеспечивает ценовую стабильность, но упускает потенциально выгодные сделки между покупателями с высокой оценкой и продавцами с высокими издержками.

Влияние на Эффективность и Производство

В основе эффективных систем лежит стремление к минимизации так называемых «затрат на перестройку» — расходов, связанных с адаптацией к новым условиям или изменениям в производственном процессе. Именно поэтому стратегии, такие как «точно в срок» (Just-in-Time Production), получили широкое распространение. Данный подход позволяет значительно сократить издержки, связанные с хранением запасов и поддержанием больших объемов производства, однако требует высокой степени координации и прогнозирования спроса. Успешное применение подобных стратегий напрямую зависит от способности системы быстро и эффективно реагировать на изменения внешней среды, а также от точности оценки потенциальных рисков, связанных с минимальными запасами и высокой зависимостью от поставщиков.

Стремление к минимизации издержек, хотя и оправданное с точки зрения эффективности, может значительно усилить негативное влияние внешних потрясений на систему. Исследования показывают, что чрезмерная оптимизация процессов и сокращение резервов ради снижения затрат делают систему более уязвимой к неожиданным изменениям в окружающей среде. В результате, даже незначительные внешние факторы могут привести к каскадным сбоям и существенным потерям. Поэтому, при проектировании и управлении сложными системами, необходимо уделять особое внимание не только эффективности, но и способности противостоять внешним воздействиям, обеспечивая достаточный уровень устойчивости и адаптивности, что требует взвешенного подхода к балансу между экономией и надежностью.

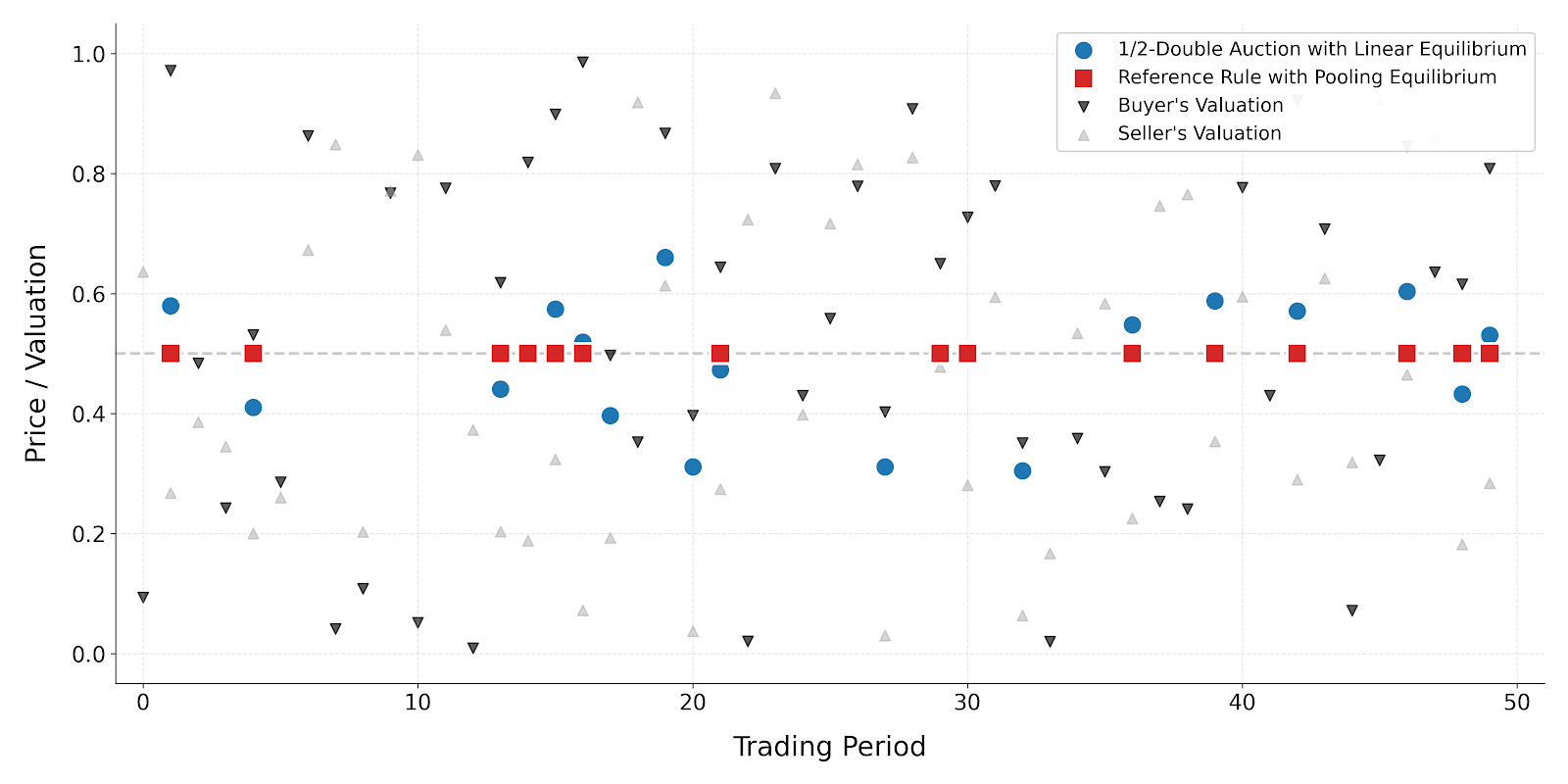
Взаимосвязь между правилами принятия решений, волатильностью и эффективностью особенно ярко проявляется в сложных рынках, функционирующих по принципу двойного аукциона. Данные механизмы, широко распространенные в финансовых кругах и торговле электроэнергией, характеризуются высокой степенью децентрализации, где участники одновременно предлагают цены на покупку и продажу. Исследования показывают, что выбор конкретного правила, определяющего поведение участников в условиях неопределенности, оказывает существенное влияние на стабильность и результативность всего рынка. В частности, неоптимальные правила могут приводить к резким колебаниям цен и снижению объемов торговли, в то время как грамотно разработанные стратегии способствуют поддержанию равновесия и повышению эффективности распределения ресурсов. Анализ показывает, что понимание этой взаимосвязи критически важно для проектирования устойчивых и продуктивных рыночных систем.

Исследования показали, что применение правила «Status Quo» — сохранения текущего состояния — в торговых системах соответствует практикам, используемым на ведущих фондовых биржах мира. Этот подход, заключающийся в предпочтении сохранения существующего порядка вещей при отсутствии явных причин для изменений, демонстрирует высокую эффективность в снижении волатильности рынка. Анализ показал, что биржи, придерживающиеся подобной стратегии, более устойчивы к внезапным колебаниям и внешним шокам, обеспечивая более предсказуемую и стабильную торговую среду. Фактически, применение этого правила позволяет минимизировать риски, связанные с резкими изменениями в ценах активов, и способствует поддержанию общего финансового баланса на рынке.

Исследование, представленное в данной работе, демонстрирует, что эффективное принятие решений в условиях неопределенности тесно связано с выявлением закономерностей и адаптацией к изменяющимся ограничениям. Особое внимание уделяется так называемым «референсным правилам», которые, как показано, позволяют минимизировать издержки корректировки и обеспечивать стабильность стратегий. Это находит отклик в словах Карла Сагана: «Мы — звездная пыль, стремящаяся понять себя». Подобно тому, как астрономы стремятся понять Вселенную, анализируя данные и выявляя скрытые закономерности, данное исследование стремится понять оптимальные стратегии, анализируя динамику изменяющихся интервалов допустимых значений и минимизируя дисперсию, что позволяет принимать взвешенные решения даже в самых сложных условиях.

Куда двигаться дальше?

Представленная работа, исследуя оптимальное принятие решений в условиях неопределенности и меняющихся ограничений, неизбежно сталкивается с вопросом о границах применимости разработанных моделей. Упор на минимизацию издержек корректировки и использование “опорных правил” выявляет закономерности, но оставляет открытым вопрос о робастности этих правил в условиях значительных отклонений от предполагаемых стохастических сред. Необходимо исследовать, как чувствительны оптимальные стратегии к неверной спецификации временных интервалов допустимых значений, и насколько эффективны адаптивные методы, позволяющие пересматривать эти интервалы в процессе обучения.

Особое внимание заслуживает расширение класса целевых функций. Минимизация дисперсии, безусловно, важна, но реальные системы часто сталкиваются с более сложными задачами, включающими компромиссы между различными критериями, такими как ожидаемая доходность, риск провала и долгосрочная устойчивость. Разработка алгоритмов, способных находить оптимальные решения в многокритериальных задачах, представляется перспективным направлением. В конечном счете, понимание системы требует не только определения оптимальных стратегий, но и осознания пределов их применимости и потенциальных ошибок.

Вполне вероятно, что дальнейшие исследования покажут, что кажущиеся “оптимальными” правила — это лишь приближения, отражающие ограничения используемых моделей и упрощений. Однако, именно в выявлении этих ограничений и заключено истинное понимание — ведь ошибка, как известно, является не провалом, а отправной точкой для нового исследования.

Оригинал статьи: https://arxiv.org/pdf/2602.15686.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-18 09:10