Управление рисками и временем: новый подход к обучению с подкреплением

Автор: Денис Аветисян

Исследование предлагает унифицированную структуру для обучения с подкреплением, позволяющую учитывать как временные факторы, так и чувствительность к риску, что повышает эффективность в сложных условиях.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал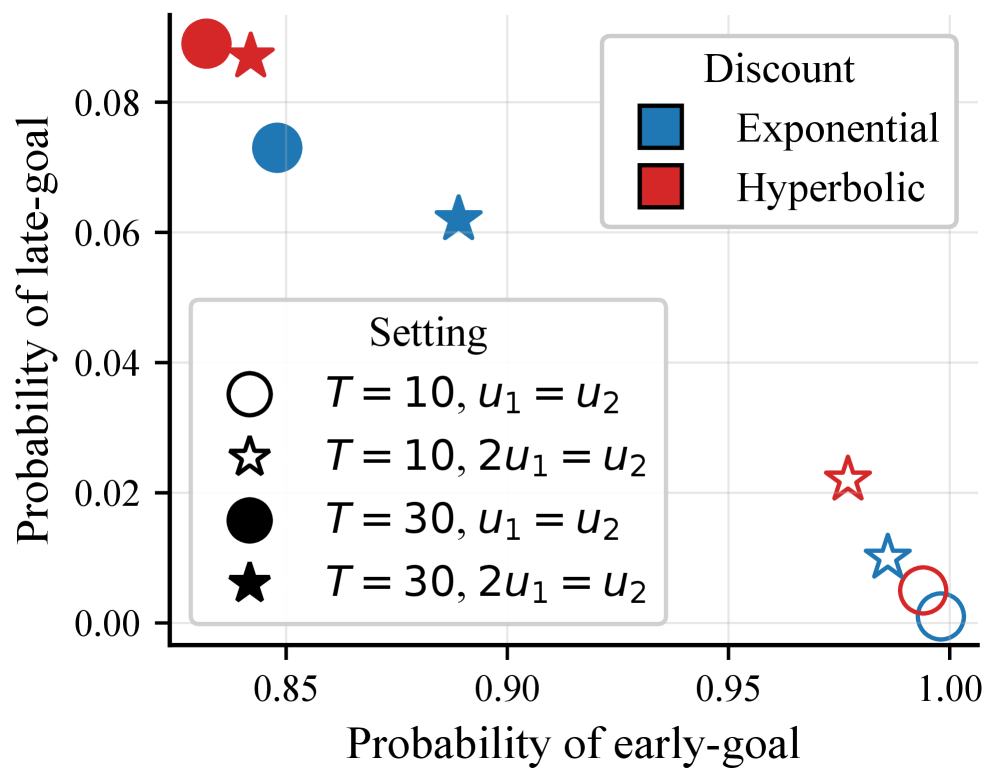

В модели принятия решений с учётом взвешенной полезности в условиях риска (GBWM) наблюдается явление обращения предпочтений, где вероятность достижения целей для агента, не склонного к риску (риск-нейтрального), и агента, чувствительного к риску, различается в зависимости от подхода к дисконтированию и особенностей среды, что демонстрирует сложность формирования последовательных стратегий в условиях неопределенности.

Представлен фреймворк для стохастического обучения с подкреплением, совместимый с общими функциями дисконтирования и функциями, учитывающими неприятие риска.

Несмотря на успехи в обучении с подкреплением, учет временных предпочтений и чувствительности к риску часто упрощается, игнорируя влияние функции дисконтирования. В работе ‘Decoupling Time and Risk: Risk-Sensitive Reinforcement Learning with General Discounting’ предложен новый подход, позволяющий отделить учет времени и риска в задачах обучения с подкреплением, используя обобщенные функции дисконтирования в рамках distributional RL. Разработанный фреймворк обеспечивает оптимизацию мер риска и решает проблемы, связанные с существующими методологиями, демонстрируя устойчивость в сложных средах. Не приведет ли это к созданию более адаптивных и безопасных систем искусственного интеллекта для критически важных приложений?

За пределами Ожидаемой Ценности: Ограничения Традиционного Обучения с Подкреплением

Традиционные алгоритмы обучения с подкреплением зачастую концентрируются на максимизации ожидаемой суммарной награды, упуская из виду полную картину возможных исходов. Такой подход, хотя и эффективен в простых сценариях, может приводить к неоптимальным решениям в условиях значительной неопределенности или риска. Вместо учета всего спектра вероятностей, алгоритм фокусируется лишь на среднем значении, игнорируя потенциальные катастрофические последствия, даже если их вероятность относительно невелика. Это упрощение, подобно игнорированию «хвостов» распределения, может привести к тому, что агент выберет стратегию, которая в среднем кажется наиболее выгодной, но при этом подвергает его неприемлемо высокому риску провала или существенных потерь. По сути, максимизация ожидаемой награды — это лишь один аспект принятия решений, и пренебрежение распределением вероятностей может существенно ограничить применимость алгоритмов обучения с подкреплением в реальных, сложных задачах.

Упрощение, заключающееся в фокусировке на максимизации ожидаемой совокупной награды, может приводить к неоптимальным решениям в условиях значительной неопределенности или риска. В ситуациях, где последствия действий непредсказуемы, а потенциальные убытки велики, агент, стремящийся лишь к среднему значению выигрыша, игнорирует критически важные аспекты распределения вероятностей. Например, в финансовом трейдинге или управлении рисками, принятие решений на основе исключительно ожидаемой прибыли может привести к катастрофическим потерям, даже если среднее значение остается положительным. Игнорирование «хвостов» распределения — редких, но потенциально разрушительных событий — лишает агента возможности эффективно управлять рисками и принимать взвешенные решения, что особенно важно в сложных, реальных сценариях, где цена ошибки может быть чрезвычайно высокой.

Существующий разрыв между моделированием поведения агента и точным отражением его склонности к риску представляет собой серьезное препятствие для применения обучения с подкреплением в сложных, реальных ситуациях. Традиционные алгоритмы зачастую оптимизируют лишь ожидаемую суммарную награду, игнорируя весь спектр возможных исходов и, следовательно, упуская из виду индивидуальные предпочтения агента в отношении риска. В результате, даже при одинаковом ожидаемом выигрыше, агент может выбирать стратегии, которые, с точки зрения человека, кажутся неоправданно рискованными или, наоборот, излишне консервативными. Это несоответствие особенно критично в сферах, где риск имеет решающее значение, таких как финансы, здравоохранение или автономное управление, где учет индивидуальных предпочтений к риску является неотъемлемой частью принятия оптимальных решений. Таким образом, преодоление этого разрыва требует разработки новых методов, способных адекватно моделировать и учитывать риск-профиль агента, обеспечивая более надежные и соответствующие человеческим ожиданиям результаты.

Предложенный метод, учитывающий временную согласованность, демонстрирует более высокую доходность в задачах торговли опционами (American Put Option) и управления лунным посадочным модулем (Windy Lunar Lander) за счет корректного моделирования нестационарной оптимальной стратегии, в отличие от подхода Fedus et al. (2019).

Распределительное Обучение с Подкреплением: Моделирование Спектра Возможностей

В отличие от стандартного обучения с подкреплением (RL), которое оценивает только ожидаемое значение будущей награды, обучение с подкреплением, основанное на распределениях (DRL), моделирует полное распределение возможных будущих наград. Это означает, что DRL не просто предсказывает среднее значение, но и оценивает вероятность получения различных значений награды. Вместо одного скалярного значения Q, DRL изучает функцию, возвращающую распределение вероятностей по возможным возвратам. Такое представление позволяет более точно оценить неопределенность и риски, связанные с каждым действием, и, следовательно, разработать более надежные и адаптивные стратегии принятия решений. Изучение распределения, а не только ожидаемого значения, предоставляет более полное представление о возможных исходах и позволяет учитывать вариативность будущих наград.

В отличие от стандартного обучения с подкреплением, которое оценивает только ожидаемое значение будущей награды, обучение с подкреплением на основе распределений (DRL) моделирует полное распределение вероятностей будущих наград. Это позволяет напрямую включать в процесс обучения предпочтения к риску агента. Например, агент может быть настроен на избежание даже небольшого риска получения низких наград, или наоборот, стремиться к высоким наградам, несмотря на потенциально высокий риск неудачи. Такой подход приводит к формированию более устойчивых и гибких политик, способных адаптироваться к различным условиям и предпочтениям, и позволяет учитывать не только среднее значение награды, но и ее дисперсию, обеспечивая более точную оценку потенциальных результатов.

Метод StockAugmentation, применяемый в Distributional Reinforcement Learning (DRL), направлен на улучшение отслеживания кумулятивных наград, что критически важно для точной оценки рисков и оптимизации политик. Суть метода заключается в создании дополнительных «стоковых» копий распределения наград, которые обновляются с использованием различных стратегий семплирования. Это позволяет более эффективно представлять и отслеживать распределение кумулятивных наград на протяжении эпизода обучения, особенно в задачах с разреженными наградами или длинными временными горизонтами. Повышенная точность отслеживания кумулятивных наград напрямую влияет на способность агента принимать решения с учетом риска, поскольку позволяет более корректно оценивать вероятность различных исходов и выбирать действия, максимизирующие ожидаемую полезность с учетом предпочтений к риску.

Временная Согласованность и Рациональные Предпочтения в Динамических Средах

Коэффициент дисконтирования γ играет ключевую роль в определении веса будущих наград при принятии решений. Традиционно используется экспоненциальное дисконтирование, предполагающее постоянную скорость дисконтирования во времени. Однако, эмпирические исследования показывают, что гиперболическое дисконтирование более точно отражает человеческие предпочтения, поскольку люди склонны отдавать предпочтение немедленному вознаграждению, даже если это означает меньшую общую выгоду в долгосрочной перспективе. В отличие от экспоненциального дисконтирования, где ценность будущей награды уменьшается экспоненциально со временем, гиперболическое дисконтирование характеризуется более резким снижением ценности на ранних этапах, что отражает склонность к импульсивности и нетерпению.

Поддержание временной согласованности — гарантия того, что оптимальный план остаётся оптимальным с течением времени — является критически важным для рационального принятия решений, особенно в контексте оптимизации политик с использованием методов Policy Optimization. Отсутствие временной согласованности приводит к нестабильности процесса обучения, поскольку оптимальное действие в текущий момент времени может измениться при рассмотрении будущего, что требует постоянной переоценки и адаптации политики. Это может привести к осцилляциям и замедлению сходимости алгоритма, поскольку агент не способен придерживаться последовательной стратегии. В алгоритмах Policy Optimization, обеспечение временной согласованности позволяет агенту формировать стабильную и предсказуемую политику, что значительно упрощает процесс обучения и повышает эффективность принимаемых решений.

Свойство временной монотонности (TimeDependentMonotonicity) операторов Беллмана обеспечивает согласованность политики агента по мере получения новой информации. В контексте динамического программирования и обучения с подкреплением, это означает, что оптимальный план, вычисленный на определенном этапе, остаётся оптимальным даже после обновления функции ценности на основе новых наблюдений. Формально, свойство гарантирует, что при увеличении горизонта планирования или доступности более полной информации, политика не будет изменяться таким образом, чтобы противоречить ранее принятым решениям. Это особенно важно для алгоритмов оптимизации политики, поскольку обеспечивает стабильность и предсказуемость поведения агента в изменяющейся среде. Отсутствие временной монотонности может привести к нестабильности обучения и неоптимальным результатам.

Алгоритм Time-Consistent обеспечивает значительное улучшение среднего вознаграждения (в среднем на 15.73% и медианно на 8.02%) в 33 из 50 игр Atari, что подтверждает преимущества поддержания временной согласованности при гиперболическом дисконтировании.

Оценка и Применение Надежного Обучения с Подкреплением в Сложных Средах

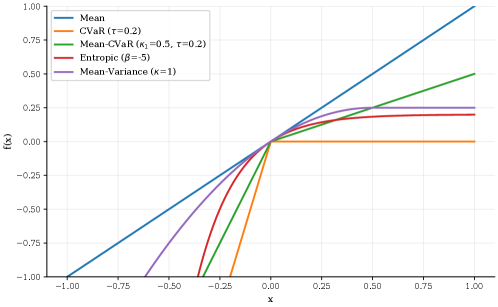
Для оценки агентов, учитывающих риски, ключевым показателем является эквивалент уверенности (Certainty Equivalent). Данный показатель представляет собой гарантированную доходность, на которую агент согласится вместо рискованной перспективы. По сути, он отражает степень неприятия риска агентом: чем ниже эквивалент уверенности по сравнению с ожидаемой доходностью рискованного варианта, тем более несклонным к риску является агент. Определение эквивалента уверенности позволяет количественно оценить, насколько сильно агент готов пожертвовать потенциальной доходностью ради избежания потерь, и служит важным инструментом при сравнении различных алгоритмов обучения с подкреплением, ориентированных на управление рисками. $CE = E[R] - \lambda \cdot Var[R]$ , где $CE$ — эквивалент уверенности, $E[R]$ — ожидаемая доходность, $Var[R]$ — дисперсия доходности, а λ — коэффициент неприятия риска.

Средняя стоимость условного отклонения (MeanCVAR) представляет собой метрику риска, широко используемую при оценке агентов, демонстрирующих нейтральность к риску (RiskNeutrality). В отличие от простых мер, таких как стандартное отклонение, MeanCVAR фокусируется на оценке ожидаемых потерь, превышающих определенный квантиль. Это позволяет более точно оценить «хвостовые» риски — потенциальные убытки, возникающие в наихудших сценариях. Таким образом, $MeanCVAR$ обеспечивает всестороннюю оценку рисков, выходя за рамки средней доходности и учитывая вероятные негативные последствия, что особенно важно в сложных и динамичных средах, где даже небольшие потери могут оказать существенное влияние на общую производительность.

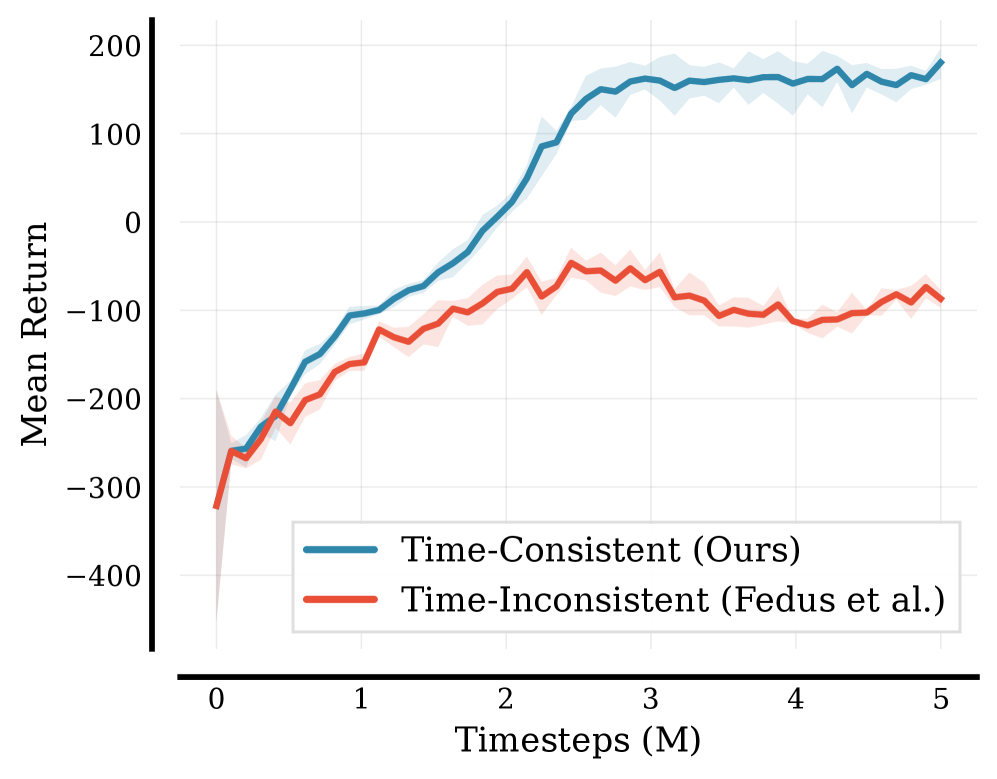
Для всесторонней оценки и подтверждения эффективности разработанных алгоритмов, тестирование проводилось на платформе AtariGames, представляющей собой набор сложных и динамичных сред. Результаты демонстрируют значительное улучшение производительности: в среднем на 39.89% и в медиане на 18.14% по 50 различным играм Atari. Алгоритмы превзошли базовый уровень в 78% случаев, что подтверждает их способность успешно адаптироваться к меняющимся условиям и достигать стабильно высоких результатов в сложных игровых сценариях. Такой подход к тестированию позволяет не только количественно оценить улучшения, но и продемонстрировать практическую применимость разработанных методов в широком спектре задач.

Различные функции полезности, используемые для оценки рисков в океанографии, подробно описаны в Приложении D.

Представленное исследование демонстрирует стремление к математической чистоте в алгоритмах обучения с подкреплением. Авторы предлагают унифицированную структуру, позволяющую согласовать функции дисконтирования и функции, учитывающие отношение к риску, что особенно важно для временной согласованности политик. Это созвучно взглядам Ады Лавлейс: “Я считаю, что машина может делать все, что может сделать человек, если только ей даны инструкции.” Подобно тому, как Лавлейс предвидела возможности вычислительных машин, данная работа стремится к созданию алгоритмов, чья корректность доказуема, а не просто эмпирически подтверждена на тестовых данных. В контексте обучения с подкреплением, это означает построение политик, которые не только максимизируют вознаграждение, но и гарантированно ведут к стабильному и предсказуемому поведению во времени, даже при использовании сложных функций дисконтирования и учета риска.

Что Дальше?

Представленная работа, хоть и демонстрирует элегантное объединение распределённого обучения с подкреплением и обобщённых функций дисконтирования, не решает фундаментальной проблемы: неизбежной апроксимации истинной функции ценности. Любое практическое применение, даже с тщательно подобранными гиперпараметрами, остаётся эмпирическим упражнением, а не доказательством корректности. Доказательство сходимости алгоритмов, особенно в условиях нелинейных функций риска и сложных пространств состояний, остаётся открытым вопросом.

Дальнейшие исследования должны быть направлены не только на повышение производительности в узкоспециализированных задачах, но и на разработку более строгих теоретических гарантий. Ирония заключается в том, что стремление к «риск-чувствительности» само по себе вносит дополнительную сложность, требуя более глубокого понимания влияния различных функций риска на стабильность и сходимость алгоритмов. Попытки «улучшить» политику, основанные исключительно на эмпирических наблюдениях, подобны строительству дворца на песке.

Будущие направления могут включать в себя исследование связей между функциями дисконтирования, функциями риска и концепцией временной согласованности. Возможно, истинная элегантность заключается не в усложнении алгоритмов, а в нахождении минимального набора предположений, необходимых для обеспечения их корректности. Иначе, мы рискуем создать ещё более сложные системы, которые будут казаться «умными», но останутся непрозрачными и уязвимыми.

Оригинал статьи: https://arxiv.org/pdf/2602.04131.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-06 02:35