Внимание нового порядка: как дробная динамика улучшает обработку последовательностей

Автор: Денис Аветисян

Новый подход к механизмам внимания в нейронных сетях позволяет эффективно моделировать взаимодействия между элементами последовательности на различных масштабах.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Удаление узлов из графа внимания с вероятностью $p$ приводит к снижению точности на тестовом наборе данных, при этом сети с $Q=K$ демонстрируют стабильную производительность, варьирующуюся в пределах стандартного отклонения, наблюдаемого в пяти повторных экспериментах, а снижение точности более выражено при увеличении размерности вклада – от 8 ($ad=8$) до 64 ($dd=64$).

В статье представлена дробная нейронная сеть внимания (FNA), вдохновленная принципами работы нейронных систем и использующая дробную динамику для повышения выразительности и эффективности трансформаторных архитектур.

Несмотря на впечатляющие успехи трансформерных моделей, понимание и расширение принципов самовнимания остаётся ключевой задачей развития искусственного интеллекта. В статье «Fractional neural attention for efficient multiscale sequence processing» предложен механизм дробного нейронного внимания (FNA), вдохновлённый многомасштабной динамикой биологического внимания и теорией динамических систем. FNA моделирует взаимодействие токенов посредством левиевского диффузионного процесса, управляемого дробным лапласианом, что позволяет эффективно учитывать зависимости между ними на различных масштабах. Способен ли этот подход, объединяющий самовнимание, стохастическую динамику и геометрию, стать основой для создания более интерпретируемых и эффективных нейросетевых архитектур?

Внимание к Масштабу: Преодолевая Ограничения Трансформеров

Архитектуры Transformer, несмотря на свою впечатляющую эффективность, сталкиваются с проблемой квадратичной сложности при увеличении длины обрабатываемой последовательности. Это означает, что вычислительные затраты и потребность в памяти растут пропорционально квадрату количества токенов в тексте, что существенно ограничивает их применимость к задачам, требующим анализа длинных документов или установления зависимостей между удалёнными фрагментами информации. Например, при обработке текста в $1000$ токенов, вычислительная сложность возрастает в $100$ раз по сравнению с текстом в $100$ токенов. Такая экспоненциальная зависимость становится критическим препятствием при работе с большими данными и долгосрочными зависимостями, препятствуя масштабированию моделей и их эффективному применению в реальных сценариях.

Суть проблемы заключается в механизме самовнимания, который требует вычисления взаимодействия между каждой парой токенов в последовательности. Это означает, что для последовательности из $n$ токенов необходимо выполнить $n^2$ операций, что приводит к квадратичной сложности. С увеличением длины последовательности, вычислительные затраты растут экспоненциально, делая обработку длинных текстов или сложных данных крайне ресурсоемкой и замедляя процесс обучения и инференса. Такой подход ограничивает возможности трансформаторов при работе с задачами, требующими анализа долгосрочных зависимостей, например, при обработке больших объемов текста или видеоданных, где контекст может простираться на значительные промежутки времени.

Ограничения вычислительных ресурсов становятся критическим фактором при обработке длинных последовательностей данных, таких как объемные текстовые документы или сложные потоки информации. Традиционные архитектуры, основанные на механизмах самовнимания, демонстрируют квадратичную сложность, что существенно замедляет обработку и требует огромных вычислительных мощностей. В этой связи, активно исследуется подход, известный как Fractional Neural Attention (FNA), стремящийся к достижению сопоставимой производительности при значительном сокращении числа параметров. FNA позволяет снизить вычислительную нагрузку, не жертвуя при этом качеством анализа данных, открывая возможности для эффективной обработки более длинных и сложных последовательностей, что особенно важно для задач, требующих понимания долгосрочных зависимостей в данных.

В ходе обучения машинного перевода, модели FNA (при α=1.2 и 2α=1.2) и Transformer (DP) демонстрируют различные показатели точности и потерь на тестовом наборе данных в зависимости от выбора параметров матрицы весов WQ,K, при этом использование WQ,K∉O(d) приводит к иным результатам по сравнению с WQ,K∈O(d), что подтверждается стандартным отклонением, отражающим стабильность обучения.

От Последовательностей к Графам: Новый Взгляд на Механизм Внимания

Представление входных данных в виде графа внимания позволяет установить более тонкие связи между токенами, в отличие от традиционной последовательной обработки. В стандартных моделях, таких как трансформеры, отношения между токенами определяются их позицией в последовательности, что ограничивает возможность моделировать сложные зависимости. Граф внимания, напротив, моделирует связи между токенами напрямую, где каждый токен представлен как узел, а ребра отражают степень их взаимосвязи, определенную механизмом внимания. Это позволяет моделировать нелокальные зависимости и учитывать контекст, выходящий за рамки непосредственной последовательности токенов, что потенциально улучшает понимание смысла и эффективность модели.

Спектральный разрыв графа внимания является показателем скорости смешивания информации, отражающим эффективность интеграции контекста в модели. Более крупный спектральный разрыв указывает на более быстрое распространение информации между токенами, что позволяет модели эффективнее учитывать взаимосвязи между ними. Экспериментальные данные показывают, что модели FNA (Frequency Normalized Attention) демонстрируют значительно больший спектральный разрыв по сравнению со стандартными трансформерами, что коррелирует с улучшенной вычислительной эффективностью и скоростью сходимости при обучении. Этот показатель позволяет количественно оценить способность модели к быстрому распространению информации и, следовательно, к более эффективной обработке последовательностей данных.

Использование графового подхода к обработке последовательностей позволяет естественным образом реализовать разреженные механизмы внимания, снижая вычислительную сложность. В моделях FNA (Frequency Normalized Attention) наблюдается сокращение средней длины кратчайшего пути между токенами по сравнению со стандартными трансформерами. Это снижение длины пути указывает на то, что информация может распространяться между токенами более эффективно, требуя меньше вычислительных ресурсов для вычисления внимания. Разреженность внимания, достигаемая благодаря графовой структуре, позволяет модели концентрироваться на наиболее релевантных связях между токенами, что приводит к уменьшению объема вычислений, необходимых для обработки последовательности, и повышению общей эффективности модели.

Исследование влияния удаления узлов из графа внимания на точность тестирования показало, что при вероятности удаления, равной <i>pp</i>, точность снижается, при этом сети с разными размерностями вложений (<i>ad</i>=8, <i>bd</i>=16, <i>cd</i>=32, <i>dd</i>=64) демонстрируют схожие тенденции, что подтверждается средними значениями, полученными в пяти испытаниях, и соответствующими областями стандартного отклонения. — Исследование влияния удаления узлов из графа внимания на точность тестирования показало, что при вероятности удаления, равной pp, точность снижается, при этом сети с разными размерностями вложений (ad=8, bd=16, cd=32, dd=64) демонстрируют схожие тенденции, что подтверждается средними значениями, полученными в пяти испытаниях, и соответствующими областями стандартного отклонения.

Разреженное Внимание в Действии: Инновации в Архитектуре Трансформеров

Архитектуры, такие как Longformer, BigBird и Nyströmformer, используют механизм локального внимания (Local Attention) для снижения вычислительных затрат. Вместо вычисления внимания между всеми парами токенов во входной последовательности, локальное внимание ограничивает область вычислений небольшими окрестностями каждого токена. Это достигается путем рассмотрения только фиксированного числа соседних токенов при вычислении весов внимания. В результате, сложность вычислений снижается с $O(n^2)$ до $O(n \cdot w)$, где $n$ – длина последовательности, а $w$ – размер окрестности. Такой подход позволяет обрабатывать значительно более длинные последовательности, сохраняя при этом приемлемую скорость вычислений.

Для сохранения осведомленности о долгосрочных зависимостях в условиях разреженного внимания, архитектуры, такие как Longformer и BigBird, комбинируют локальное внимание с глобальными токенами или ядрами, основанными на ориентирах. Глобальные токены, как правило, представляют собой специально выделенные позиции, которые учитываются всеми остальными токенами, обеспечивая прямой доступ к информации на всем протяжении последовательности. Альтернативно, landmark-based kernels используют выборку наиболее важных позиций (ориентиров) для представления последовательности, что позволяет эффективно моделировать долгосрочные зависимости с меньшими вычислительными затратами. Такой подход позволяет снизить вычислительную сложность, сохраняя при этом способность моделировать отношения между удаленными элементами последовательности, что критически важно для задач, требующих понимания контекста на больших расстояниях.

Эффективность механизмов разреженного внимания демонстрирует возможность масштабирования Transformer-архитектур для обработки существенно более длинных последовательностей. Практическое подтверждение этому предоставляет модель FNA (Fast Neural Attention), которая достигает сопоставимой производительности со стандартными Transformer-моделями в задачах классификации текста. Это указывает на то, что разреженное внимание является жизнеспособной альтернативой полному вниманию, позволяя существенно снизить вычислительные затраты при сохранении или даже улучшении точности в определенных сценариях, что критически важно для задач, требующих обработки длинных текстов, таких как анализ документов или машинный перевод.

Многообразия и Диффузия: Представление Геометрии Данных

Данные, с которыми сталкиваются в различных областях науки и техники, зачастую не распределены равномерно в многомерном пространстве, а сконцентрированы на римановом многообразии – сложной геометрической структуре. Представьте себе поверхность мяча: движение по ней ограничено кривизной, и расстояние между точками измеряется не прямой линией, проходящей сквозь центр Земли, а кратчайшим путем по поверхности. Аналогично, данные на римановом многообразии подчиняются собственной геометрии, что существенно влияет на то, как информация распространяется между точками данных. Эта внутренняя геометрия определяет, какие направления более «легкие» для движения информации, а какие – затруднены, что, в свою очередь, влияет на эффективность алгоритмов машинного обучения и анализа данных. Понимание этой геометрии является ключевым для разработки методов, способных эффективно обрабатывать и интерпретировать сложные данные.

Карты диффузии используют представление о том, что данные часто располагаются на римановом многообразии, и моделируют распространение информации как стохастический процесс. Этот подход позволяет улавливать внутреннюю размерность данных, то есть количество действительно значимых параметров, определяющих их структуру. В основе метода лежит идея о том, что информация распространяется не хаотично, а подчиняется определенной геометрии пространства данных. Представляя данные как результат диффузии, подобно тому, как частицы рассеиваются в жидкости, алгоритм может эффективно уменьшить размерность, сохраняя при этом наиболее важные характеристики. В результате, сложные данные могут быть представлены в более компактном и информативном виде, что упрощает задачи классификации и анализа, позволяя выявлять скрытые закономерности и взаимосвязи, которые были бы не видны при использовании традиционных методов.

Сравнение броуновского движения – простого случайного блуждания – с диффузией Леви демонстрирует критическую важность понимания лежащего в основе процесса диффузии для построения эффективных представлений данных. В отличие от броуновского движения, описываемого гауссовым распределением вероятностей, диффузия Леви учитывает “скачки” – внезапные перемещения на большие расстояния, что позволяет более точно моделировать сложные данные. Результаты исследований подтверждают эту концепцию: модель FNA, использующая принципы диффузии Леви, достигает 76.17% точности в задаче классификации изображений CIFAR-10, превосходя стандартные архитектуры Transformers. Это свидетельствует о том, что учет особенностей диффузионного процесса позволяет создавать более мощные и эффективные модели для анализа и обработки данных, особенно в задачах, связанных с визуальной информацией и сложными геометрическими структурами.

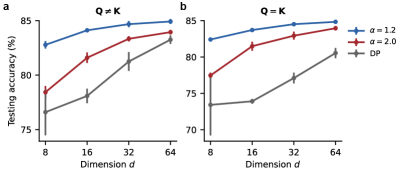
Эксперименты показали, что точность на тестовом наборе данных зависит от размерности встраивания и глубины модели, причем для случаев, когда матрицы запросов и ключей различны (𝐐≠𝐊), наблюдается выраженная зависимость, подтвержденная средними значениями и стандартными отклонениями, полученными в ходе пяти повторных испытаний, а при равенстве матриц запросов и ключей (𝐐=𝐊) эта зависимость сохраняется.

Исследование, представленное в статье, демонстрирует, что традиционные механизмы внимания в Transformer-архитектурах часто упускают из виду взаимодействия между токенами на различных масштабах. Введение Фракционального Нейронного Внимания (FNA) – это попытка преодолеть это ограничение, используя принципы, заимствованные из динамических систем и нейробиологии. Этот подход позволяет моделировать зависимости между токенами более гибко и эффективно. Как однажды заметил Дональд Дэвис: «Время — не метрика, а среда, в которой существуют системы». Действительно, FNA рассматривает последовательности не как статичные структуры, а как динамически развивающиеся системы, где взаимодействия между элементами происходят во времени и на различных уровнях масштаба, что позволяет более точно отражать сложность и изменчивость реальных данных.

Куда же дальше?

Предложенный механизм внимания, вдохновленный динамикой нейронных систем и, что примечательно, стохастическими процессами Леви, представляет собой любопытную попытку преодолеть присущие трансформерам ограничения в обработке последовательностей. Однако, следует признать, что сама идея “фрактального” внимания – это лишь первый шаг. Неизбежно возникает вопрос о масштабируемости предложенного подхода к действительно длинным последовательностям, где вычислительные издержки, связанные с вычислением дробных лапласианов, могут нивелировать все преимущества. Архитектура без истории – хрупка и скоротечна, и будущее потребует более глубокого понимания того, как адаптировать эти механизмы к задачам, требующим длительной памяти.

Очевидным направлением дальнейших исследований представляется изучение взаимодействия дробного внимания с другими механизмами, такими как разреженное внимание или рекуррентные нейронные сети. Каждая задержка – цена понимания, и необходимо выяснить, возможно ли комбинирование этих подходов для создания более эффективных и выразительных моделей. Более того, не стоит забывать о биологической правдоподобности – насколько предложенный механизм действительно отражает принципы работы мозга, и какие еще нейробиологические инсайты могут быть использованы для улучшения архитектур искусственного интеллекта.

В конечном счете, все системы стареют – вопрос лишь в том, делают ли они это достойно. Предложенный подход – это не панацея, а скорее еще один инструмент в арсенале исследователей, стремящихся создать более интеллектуальные и устойчивые системы обработки информации. Время – не метрика, а среда, в которой существуют системы, и только время покажет, насколько успешным окажется этот новый путь.

Оригинал статьи: https://arxiv.org/pdf/2511.10208.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-11-15 15:54